41.线性分类器与非线性分类器的区别以及优劣
如果模型是参数的线性函数,并且存在线性分类面,那么就是线性分类器,否则不是。
常见的线性分类器有:LR,贝叶斯分类,单层感知机、线性回归
常见的非线性分类器:决策树、RF、GBDT、多层感知机
SVM两种都有(看线性核还是高斯核)
线性分类器速度快、编程方便,但是可能拟合效果不会很好
非线性分类器编程复杂,但是效果拟合能力强
42.数据的逻辑存储结构(如数组,队列,树等)对于软件开发具有十分重要的影响,试对你所了解的各种存储结构从运行速度、存储效率和适用场合等方面进行简要地分析。
运行速度存储效率适用场合数组快高比较适合进行查找操作,还有像类似于矩阵等的操作链表较快较高比较适合增删改频繁操作,动态的分配内存队列较快较高比较适合进行任务类等的调度栈一般较高比较适合递归类程序的改写二叉树(树)较快一般一切具有层次关系的问题都可用树来描述图一般一般除了像最小生成树、最短路径、拓扑排序等经典用途。还被用于像神经网络等人工智能领域等等。
43.什么是分布式数据库?
分布式数据库系统是在集中式数据库系统成熟技术的基础上发展起来的,但不是简单地把集中式数据库分散地实现,它具有自己的性质和特征。集中式数据库系统的许多概念和技术,如数据独立性、数据共享和减少冗余度、并发控制、完整性、安全性和恢复等在分布式数据库系统中都有了不同的、更加丰富的内容。
44.简单说说贝叶斯定理。 在引出贝叶斯定理之前,先学习几个定义:
- 条件概率(又称后验概率)就是事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在B条件下A的概率”。
比如,在同一个样本空间Ω中的事件或者子集A与B,如果随机从Ω中选出的一个元素属于B,那么这个随机选择的元素还属于A的概率就定义为在B的前提下A的条件概率,所以:P(A|B) = |A∩B|/|B|,接着分子、分母都除以|Ω|得到
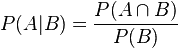
联合概率表示两个事件共同发生的概率。A与B的联合概率表示为
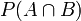
或者
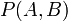
。
边缘概率(又称先验概率)是某个事件发生的概率。边缘概率是这样得到的:在联合概率中,把最终结果中那些不需要的事件通过合并成它们的全概率,而消去它们(对离散随机变量用求和得全概率,对连续随机变量用积分得全概率),这称为边缘化(marginalization),比如A的边缘概率表示为P(A),B的边缘概率表示为P(B)。
接着,考虑一个问题:P(A|B)是在B发生的情况下A发生的可能性。
1.首先,事件B发生之前,我们对事件A的发生有一个基本的概率判断,称为A的先验概率,用P(A)表示;
2.其次,事件B发生之后,我们对事件A的发生概率重新评估,称为A的后验概率,用P(A|B)表示;
3.类似的,事件A发生之前,我们对事件B的发生有一个基本的概率判断,称为B的先验概率,用P(B)表示;
4.同样,事件A发生之后,我们对事件B的发生概率重新评估,称为B的后验概率,用P(B|A)表示。
贝叶斯定理便是基于下述贝叶斯公式:
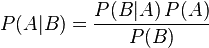
上述公式的推导其实非常简单,就是从条件概率推出。
根据条件概率的定义,在事件B发生的条件下事件A发生的概率是
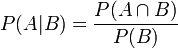
同样地,在事件A发生的条件下事件B发生的概率
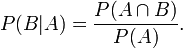
整理与合并上述两个方程式,便可以得到:
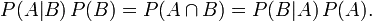
接着,上式两边同除以P(B),若P(B)是非零的,我们便可以得到贝叶斯定理的公式表达式:
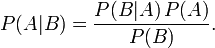
所以,贝叶斯公式可以直接根据条件概率的定义直接推出。即因为P(A,B) = P(A)P(B|A) = P(B)P(A|B),所以P(A|B) = P(A)P(B|A) / P(B)。更多请参见此文http://blog.csdn.net/v_july_v/article/details/40984699
45.#include和#include“filename.h”有什么区别? 用 #include 格式来引用标准库的头文件(编译器将从标准库目录开始搜索)。
用 #include “filename.h” 格式来引用非标准库的头文件(编译器将从用户的工作目录开始搜索)。