正规表达式的实现原理
上文讨论了串的模式的表达,即正规表达式。那么这一小节将讨论我们实现一个正规表达式的方法和原理。因为我们知道,一个正规表达式对应着一个串模式,而一个串模式又对应着一些列符合该模式描述的规则的串。那么,我们是否可以通过实现出正规表达式,从而实现对一个给定串的判别呢?答案是肯定的。
状态转换图
首先介绍,状态转换图。
状态转换图是一个有向图,由节点和边组成。每个节点代表一个状态,状态之间用箭头连接,称为边。边上的字符表示从该边的出发节点读取一个该边上的字符后,可以抵达改变指向的状态节点。如下图:
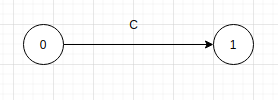
状态转换图中具有一个状态标记为 start 状态,被称为初始状态。识别一个字符串时,我们就从这个状态开始。下图展示了能够识别 大于号 或者 大于等于号 的状态转换图:
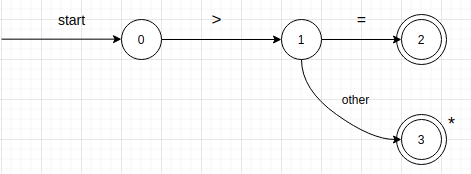
其开始状态是状态 0,在状态 0 读入下一个字符,如果该字符是 > ,那么则转向状态 1,否则失败。在状态 1 时,读入下一个字符,如果是 + ,则转向状态 2,否则标有 other 的边表明转向状态 3.在状态 2 上有双圈,表示它是接受状态。当进入这个状态时,状态转换图识别了记号 >= 。
通常会有多个状态转换图,每个状态转换图对应者一个类别(如记号)。如果沿着一个状态转换图书别串时失败,那么就需要将前向指针回退到该状态图开始状态时该指针所指向的输入串的位置。并启动下一个状态转换图,试图匹配下一个模式。显然,我们可以通过不断的组合状态转换图来实现更加复杂的串模式匹配。可以说,状态转换图为串模式识别提供了一种有效方法。
所以状态转换图实现了正规表达式和图结构的转换。上面的状态转换图对应着正规表达式:>((epsilon)|=) 。而图结构十分容易使用计算机实现。
有穷自动机
有穷自动机是更一般化的状态转换图。它可以是确定的即 DFA,也可以是不确定的即 NFA。其中“不确定”的含义是:对于某个输入符号,在同一个状态上存在不止一种转换。我们可以通过构造有穷自动机把正规表达式编译成识别器。二者都可以识别且仅能识别正规集,即能够识别正规表达式所表示的字符串集合。但是二者有着时空上的权衡,DFA 导出的识别器比NFA导出的识别器要快得多,但DFA可能比与之等价的NFA大得多。(注:NFA,DFA 的数学模型定义这里从略)
NFA
由于从正规式转换成不确定的有穷自动机(NFA)更方便,所以先讨论 NFA。
下图是一个 NFA:

它所对应的正规表达式为:(a|b)*abb 。注意,NFA 是用带标记的有向图表示,称为转换图,节点是状态,有标记的边是转换关系。NFA 这种转换图与之前的状态转换图很类似,但是区别是:同一个字符可以标记始于同一个状态的两个或多个转换,边上可以有输入字符符号,也可以有特殊符号 (epsilon) 。
从正规表达式构造 NFA
这里采用一个简单的算法来实现这种构造。首先构造自动机使其能够识别任何 (epsilon) 的字母表中的任何符号,然后由此构造自动机来识别包含一个交、一个连接或者一个克林闭包运算符的正规表达式。如对于正规表达式:a|b 可以先分别构造字符 a 和 b 的自动机,然后在从二者的 NFA 构造出 a|b 的 NFA。该算法被称为 Thompson 构造法。