这道题出自LeetCode,题目如下:
在二叉树中,根节点位于深度 0 处,每个深度为 k 的节点的子节点位于深度 k+1 处。
如果二叉树的两个节点深度相同,但 父节点不同 ,则它们是一对堂兄弟节点。
我们给出了具有唯一值的二叉树的根节点 root ,以及树中两个不同节点的值 x 和 y 。
只有与值 x 和 y 对应的节点是堂兄弟节点时,才返回 true 。否则,返回 false。
示例 1:
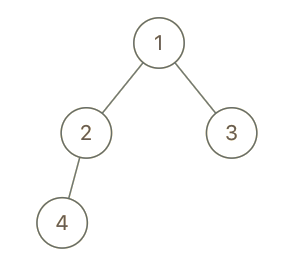
输入:root = [1,2,3,4], x = 4, y = 3
输出:false
示例 2:
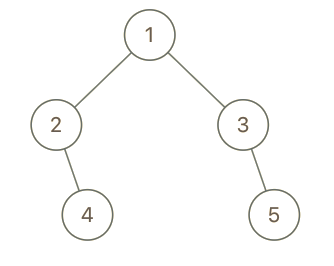
输入:root = [1,2,3,null,4,null,5], x = 5, y = 4
输出:true
示例 3:
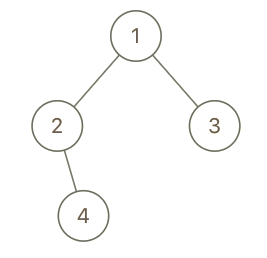
输入:root = [1,2,3,null,4], x = 2, y = 3
输出:false
提示:
二叉树的节点数介于
2到100之间。
每个节点的值都是唯一的、范围为1到100的整数。
容易发现,这道题本质上是BFS,但有两个问题需要解决:首先如何判断队列中要访问的节点是处于同一层,即深度是否相同;其次,如何判断它们的父节点是否相同。
为了解决这两个问题,我们需要在访问队列中的一个节点时,预先查看一下它的子节点是否是要找的节点。如果是;那我们需要记录一下这个节点对应的父节点指针。这样,当要判断的两个节点都找到的时候,比较一下对应记录的父节点指针,即可得知它们的父节点是否相同。
至于如何判断两个节点是否在同一层,根据BFS的性质,访问一个节点时,会将其从队列中移除,然后将它的子节点加入队列。我们可以预先算出每一层节点的数量,每次移除节点时检查当前层剩余节点数量。当某一层遍历完时,如果只找到了其中某一个节点,那么必定这两个节点不是堂兄弟节点了。
最后通过的完整代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isCousins(TreeNode* root, int x, int y) {
queue<TreeNode *> q;
q.push(root);
int curLevel = 1;
int nextLevel = 0;
TreeNode *xParent = nullptr;
TreeNode *yParent = nullptr;
while(!q.empty())
{
TreeNode *p = q.front();
q.pop();
curLevel--;
TreeNode *pl = p->left;
if(pl)
{
if(pl->val == x)
{
xParent = p;
}
else if(pl->val == y)
{
yParent = p;
}
q.push(pl);
nextLevel++;
}
TreeNode *pr = p->right;
if(pr)
{
if(pr->val == x)
{
xParent = p;
}
else if(pr->val == y)
{
yParent = p;
}
q.push(pr);
nextLevel++;
}
if(xParent && yParent)
{
return xParent != yParent;
}
if(curLevel == 0)
{
if(xParent || yParent)
{
return false;
}
curLevel = nextLevel;
nextLevel = 0;
}
}
return false;
}
};