删点成林

这道题出自LeetCode，题目如下：

给出二叉树的根节点 root，树上每个节点都有一个不同的值。

如果节点值在 to_delete 中出现，我们就把该节点从树上删去，最后得到一个森林（一些不相交的树构成的集合）。

返回森林中的每棵树。你可以按任意顺序组织答案。

示例：

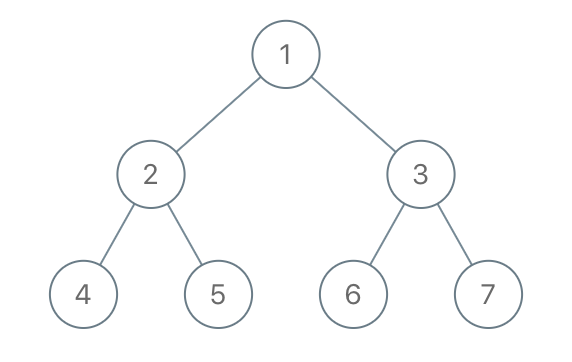
输入：root = [1,2,3,4,5,6,7], to_delete = [3,5]
输出：[[1,2,null,4],[6],[7]]

提示：

• 树中的节点数最大为 1000。
• 每个节点都有一个介于 1 到 1000 之间的值，且各不相同。
• to_delete.length <= 1000
• to_delete 包含一些从 1 到 1000、各不相同的值。

这道题显然是跟树遍历有关的问题，因为这里需要考虑到节点之间的父子关系，所以采用DFS遍历比较合适。针对这道题，DFS又分前序遍历（即先遍历根节点）和后序遍历（即最后遍历根节点）两种方式，让我们先从前序遍历看起。首先，根据题目假设，每个节点的值是不重复的，所以我们可以将要删除的节点存到set中去，这样可以加快查询速度：

set<int> keys;

for(int k : to_delete)
{
    keys.insert(k);
}

其次，问题的重点在于先序遍历如何定位到可以被加入到森林中的节点。通过观察不难发现，如果当前遍历到的节点不在删除列表中，且它的父节点在删除列表中，它才可以被加入到森林中去：

void dfs(TreeNode* root, set<int>& keys, bool pDelete, vector<TreeNode*> &res)
{
    if(!root)
    {
        return;
    }

    bool rDelete = keys.count(root->val) != 0;
    if(pDelete && !rDelete)
    {
        res.push_back(root);
    }

    dfs(root->left, keys, rDelete, res);
    dfs(root->right, keys, rDelete, res);
}

代码中，pDelete代表当前节点的父节点是否要被删除，rDelete代表当前节点是否要被删除。

除此之外，我们还需要解决一个问题，就是要修改二叉树的结构。当一个节点被删除时，它的父节点对应指向它的left指针或者right指针要置为空。这里有个比较巧妙的做法，就是让递归函数返回一个指针，表示修改过后的节点，如果这个节点被删除了，那么返回的就是空指针，这样上层调用该函数时，直接覆盖对应的left指针或者right指针即可：

TreeNode* dfs(TreeNode* root, set<int>& keys, bool pDelete, vector<TreeNode*> &res)
{
    if(!root)
    {
        return nullptr;
    }

    bool rDelete = keys.count(root->val) != 0;
    if(pDelete && !rDelete)
    {
        res.push_back(root);
    }

    root->left = dfs(root->left, keys, rDelete, res);
    root->right = dfs(root->right, keys, rDelete, res);

    if(rDelete)
    {
        return nullptr;
    }
    else
    {
        return root;
    }
}

返回指针还有一个好处，就是在第一次二叉树的根节点调用该函数时，得到的是修改过的根节点指针，如果指针为空，说明根节点被删除了，就无需将根节点加入到最后的森林列表中：

root = dfs(root, keys, false, res);
if(root)
{
	res.push_back(root);
}

最终通过的代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<TreeNode*> delNodes(TreeNode* root, vector<int>& to_delete) {
        vector<TreeNode*> res;

        set<int> keys;

        for(int k : to_delete)
        {
            keys.insert(k);
        }

        root = dfs(root, keys, false, res);
        if(root)
        {
            res.push_back(root);
        }
        return res;
    }

    TreeNode* dfs(TreeNode* root, set<int>& keys, bool pDelete, vector<TreeNode*> &res)
    {
        if(!root)
        {
            return nullptr;
        }

        bool rDelete = keys.count(root->val) != 0;
        if(pDelete && !rDelete)
        {
            res.push_back(root);
        }

        root->left = dfs(root->left, keys, rDelete, res);
        root->right = dfs(root->right, keys, rDelete, res);

        if(rDelete)
        {
            return nullptr;
        }
        else
        {
            return root;
        }
    }
};

后序遍历的方式其实就更简单了，如果当前的节点是需要删除的，那么就把它的子节点加入到森林中。因为后序遍历先遍历的是它的子节点，所以如果子节点也被删除了，那么返回回来的就是空指针，就不必加入到森林里。

最终通过的代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<TreeNode*> delNodes(TreeNode* root, vector<int>& to_delete) {
        vector<TreeNode*> res;

        set<int> keys;

        for(int k : to_delete)
        {
            keys.insert(k);
        }

        root = dfs(root, keys, res);
        if(root)
        {
            res.push_back(root);
        }
        return res;
    }

    TreeNode* dfs(TreeNode* root, set<int>& keys, vector<TreeNode*> &res)
    {
        if(!root)
        {
            return nullptr;
        }

        root->left = dfs(root->left, keys, res);
        root->right = dfs(root->right, keys, res);

        bool rDelete = keys.count(root->val) != 0;
        if(rDelete)
        {
            if(root->left)
            {
                res.push_back(root->left);
            }
            if(root->right)
            {
                res.push_back(root->right);
            }
            return nullptr;
        }
        else
        {
            return root;
        }
    }
};