Deep Residual Learning for Image Recognition
Kaiming He Xiangyu Zhang Shaoqing Ren Jian Sun
摘要
更深层次的神经网络更难训练。我们提出了一个残差学习框架,以简化对比以前使用的网络更深入的网络的训练。我们根据层输入显式地将层重新表示为学习残差函数( learning residual functions),而不是学习未定义函数。我们提供了综合的经验证据,表明这些残差网络易于优化,并且可以从大幅度增加的深度中获得精度。在ImageNet数据集上,我们估计残差网络的深度可达152层--是vgg网络的8倍深[41],但仍然具有较低的复杂性。这些残差网的集合在图像集上的误差达到了3.57%。 这个结果获得了ILSVRC2015的分类任务第一名,我们还用CIFAR-10数据集分析了100层和1000层的网络。
表示的深度对于许多视觉识别任务是非常重要的。仅仅由于我们的表示非常深入,我们在coco对象检测数据集上得到了28%的相对改进。 深度残差网络是我们参加ILSVRC & COCO 2015 竞赛上所使用模型的基础,并且我们在ImageNet检测、ImageNet定位、COCO检测以及COCO分割上均获得了第一名的成绩。
1 介绍
在深度重要性的驱动下,出现了一个问题:学习更好的网络就像堆积更多的层一样容易吗?回答这个问题的一个障碍是臭名昭著的梯度消失/爆炸[1,9]的问题,它从一开始就阻碍了收敛(hamper convergence )。然而,这个问题在很大程度上是通过标准化初始化[23,9,37,13]和中间归一化层[16]来解决的,这使得数十层的网络在反向传播的随机梯度下降(SGD)上能够收敛。
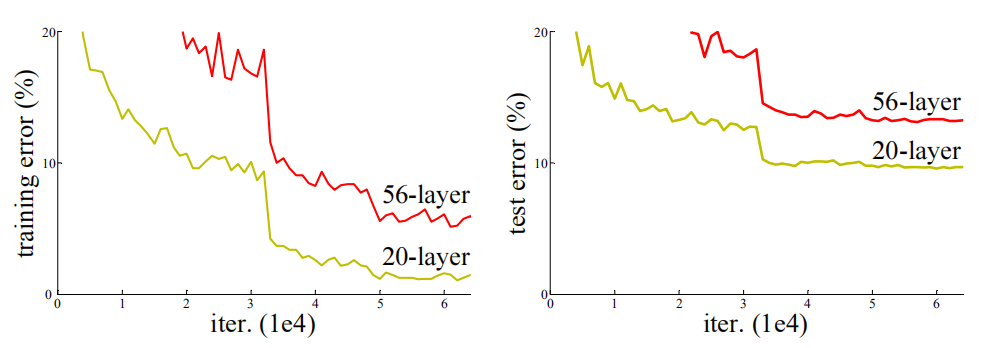
图1 20层和56层的“简单”网络在CIFAR-10上的训练误差(左)和测试误差(右)。更深的网络有更高的训练误差和测试误差。ImageNet上的类似现象如图4所示。
当更深的网络能够开始收敛时,一个退化的问题就暴露出来了:随着网络深度的增加,精确度变得饱和(这可能不足为奇),然后迅速退化。出乎意料的是,这种退化并不是由于过度拟合造成的,而且在适当深度的模型中增加更多的层会导致更高的训练误差,正如[11,42]中所报告的,并通过我们的实验进行了彻底验证。图1显示了一个典

图2. 残差学习:构建块
3.57% top-5的错误率,并在ILSVRC 2015分类比赛中获得了第一名。极深的表示在其它识别任务中也有极好的泛化性能,并带领我们在进一步赢得了第一名:包括ILSVRC & COCO 2015竞赛中的ImageNet检测,ImageNet定位,COCO检测和COCO分割。坚实的证据表明残差学习准则是通用的,并且我们期望它适用于其它的视觉和非视觉问题。2. 相关工作
3. 深度残差学习
3.1. 残差学习
在实际情况下,恒等映射不太可能是最优的,但是我们的重新表达对于这个问题的预处理是有帮助的。如果最优函数更接近于恒等映射而不是零映射,则求解者应该更容易找到与恒等映射有关的扰动(perturbations),而不是将其作为新的扰动来学习。我们通过实验(图7)证明了学习的残差函数一般都有较小的响应,说明恒等映射提供了合理的预条件
3.2 通过快捷方式进行恒等映射
我们对每几个层叠的层次采用残差学习。图2中展示出了一个积木块(building block )。形式上,在本文中,我们考虑了一个积木块被定义为:
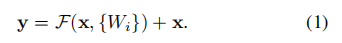
这里x和y是考虑的层的输入和输出向量。函数表示要学习的残差映射。 图2中的例子包含两层,
,其中σσ代表ReLU,为了简化省略了偏置项。F+xF+x操作由一个快捷连接和元素级(element-wise)的加法来表示。在加法之后我们再执行另一个非线性操作(例如, σ(y)σ(y),如图2)。
Eq.1中的shortcut连接没有增加额外的参数和计算复杂度。这不仅在实践中很有吸引力,而且在我们比较普通网络和残差网络时也很重要。 我们可以在参数、深度、宽度以及计算成本都相同的基础上对两个网络进行公平的比较(除了可以忽略不计的元素级的加法)。
在eqn.(1)中,x和F的维数必须相等。如果情况并非如此(例如,在更改输入/输出通道时),我们可以通过快捷连接执行线性投影W s ,以匹配维度:
![]()
我们还可以在eqn(1)中使用方阵Ws。但是,我们将通过实验证明,恒等映射对于解决退化问题是足够的,而且是经济的,因此只有在匹配维数时才使用Ws。
残差函数F的形式是灵活的。本文的实验涉及一个函数F,它有两个或三个层(图5),然而它可能有更多的层。但如果F只有一个单层,则eqn.(1)类似于线性层:y=w1x+x,对此我们没有发现任何优势。
我们还注意到,虽然为了简单起见,上述表示法是关于全连通层的,但它们适用于卷积层。函数F(x,{wi})可以表示多个卷积层.元素级加法是在两个特征映射上相应通道上执行的。
3.3 网络结构
我们测试了各种普通/残差网络,并观察到一致的现象。为了提供讨论的实例,我们对ImageNet的两个模型进行了如下描述。
Plain网络。我们的plain网络结构(图3,中)主要受VGG网络 (图.3,左)的启发。卷积层主要为3*3的滤波器,并遵循以下两点要求:(i) 输出特征映射尺寸相同的层含有相同数量的滤波器;(ii) 如果特征尺寸减半,则滤波器的数量增加一倍来保证每层的时间复杂度相同。我们直接用步长为2的卷积层进行下采样。网络以一个全局平均池层和一个带有Softmax的1000路全连接层结束。在图3(中),有权值的层的总数为34 。
值得注意的是,与vgg网[41](图3,左)相比,我们的模型具有更少的滤波器和更低的复杂度。我们的34层基线(baseline)有36亿FLOPs乘加),仅为VGG-19(196亿FLOPs)的18%。

图3 对应于ImageNet的网络框架举例。 左:VGG-19模型 (196亿个FLOPs)作为参考。中:plain网络,含有34个参数层(36 亿个FLOPs)。右:残差网络,含有34个参数层(36亿个FLOPs)。虚线表示的shortcuts增加了维度。Table 1展示了更多细节和其它变体。
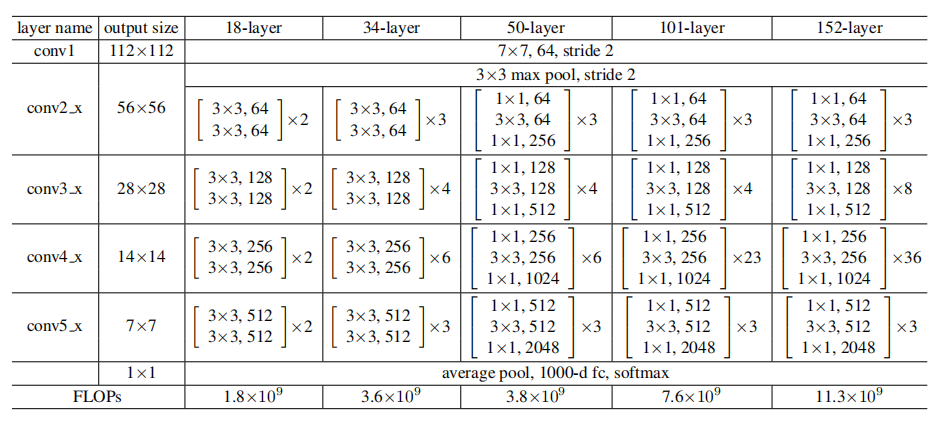
表1. 对应于ImageNet的结构框架。括号中为构建块的参数(同样见Fig.5),数个构建块进行堆叠。下采样由stride为2的conv3_1、conv4_1和conv5_1 来实现。
残差网络。基于上述plain网络,我们插入快捷连接(图3,右)将网络转换为对应的残差版本。当输入和输出尺寸相同时(图3中的实线快捷连接),可以直接使用恒等快捷键(eqn.1)。 当维度增加时(Fig.3中的虚线部分),考虑两个选项: (A) shortcut仍然使用恒等映射,在增加的维度上使用0来填充,这样做不会增加额外的参数; (B) 使用Eq.2的映射shortcut来使维度保持一致(通过1*1的卷积)。 对于这两个选项,当shortcut跨越两种尺寸的特征图时,均使用stride为2的卷积。
3.4 实现
我们对ImageNet的实现遵循了[21,41]中的做法。 调整图像的大小使它的短边长度随机的从[256,480] 中采样来进行尺寸扩展( scale augmentation)[41]。 从图像或其水平翻转中随机抽取224×224 crop,并减去每个像素平均(the per-pixel mean)[21]。使用了[21]中的标准颜色增强。我们遵循[16],在每次卷积之后,在激活之前采用批归一化(BN)[16]。我们像[13]一样初始化权重,从零开始训练所有plain/残差网。我们使用小批量大小为256的SGD。学习速率从0.1开始,当误差稳定时除以10,并且 整个模型进行60∗10^4次迭代训练。我们使用的权重衰减为0.0001,动量为0.9。我们不使用Dropout[14],按照[16]的做法。
在测试中,为了进行比较,我们采取标准的10-crop测试。 为了取得最好的效果,我们采用了[41,13]中的全卷积形式,并且在多尺度上平均分数(图像被调整大小,使较短的一面为{224,256,386,480,640})。
4 实验
4.1 ImageNet分类
我们在ImageNet 2012分类数据集[36]上评估了我们的方法,该数据集包含1000个类。模型在128万张训练图像上进行了巽寮,在50k验证图像上进行了评估。我们还获得了测试服务器报告的100 k张测试图像的最终结果。我们评估了前1位和前5位的错误率(top-1 and top-5 error rates)。
普通的网络。我们首先评估18层和34层普通网。34层普通网在图3(中)。18层普通网具有类似的形式.详细的体系结构见表1。
表2的结果表明,较深的34层普通网比较浅的18层普通网具有更高的验证误差。为了揭示原因。在图4(左)中,我们在训练过程中比较他们的训练/验证错误。我们在整个训练过程中观察到了34层普通网的退化问题---它在整个训练过程中训练误差较大,尽管18层普通网的解空间( solution space)是34层普通网的子空间。
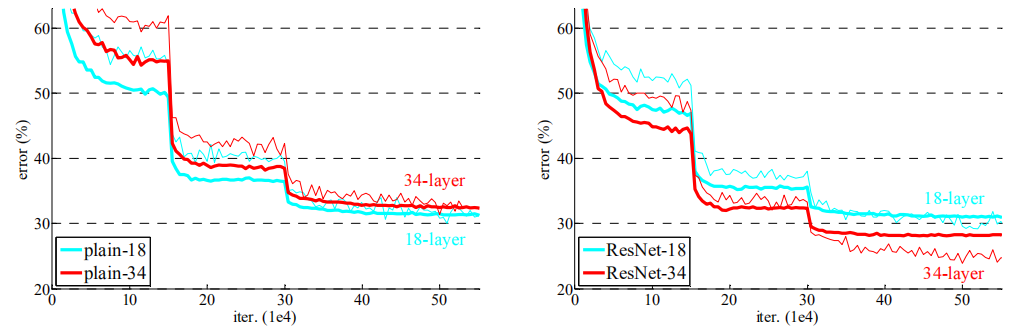
图4、关于ImageNet的训练。细曲线表示训练误差,粗体曲线表示中心crop的验证误差。左:18层和34层的普通网络。右:18层和34层残差网络。在此图中,与普通网络相比,残差网络没有(增加)额外的参数。
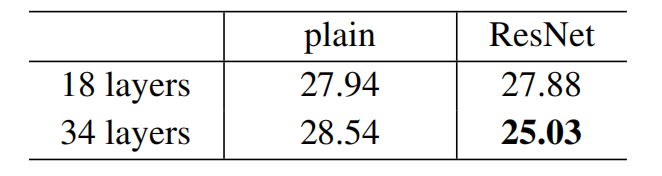
表2、ImageNet验证上的Top-1错误(%,10-crop 测试)。在这里,与普通的对等网相比,残差网没有额外的参数。图4展示了培训过程。
我们认为这种优化困难不太可能是由梯度消失引起的。这些简单的网络使用BN[16]进行训练,从而确保前向传播的信号具有非零方差。我们还验证了使用BN的向后传播梯度具有健康的行为(norms)。所以无论向前还是向后信号都不会消失。事实上,34层普通网仍然能够达到具有竞争力的精度(表3),这表明求解器在某种程度上可以工作。我们推测深普通网可能具有指数级别的低收敛速度,从而影响训练误差的减小【3--我们已经试验了更多的训练迭代(3×),并仍然观察到退化问题,这表明这个问题不可能通过简单地使用更多的迭代来解决】。这种优化困难的原因将在今后进行研究。
残差网络。接下来,我们评估18层和34层残差网(ResNet).基线结构与上述普通网相同,只是要求在每对3×3过滤器中添加一个快捷连接,如图3(右)所示。在第一个比较中(表2和图4右),我们使用所有快捷方式为恒等映射,以及使用零填充增加维度(选项A)。因此,与普通的对应网络相比,它们没有额外的参数。
我们从表2和图4中有三个主要的观察结果。首先,使用残差学习的情况与之前(普通网)相反----34层ResNet优于18层 ResNet(2.8%).更重要的是,34层ResNet的训练误差要小得多,并且可以推广到验证数据.这表明,在这种情况下,退化问题得到了很好的解决,并且我们设法从增加的深度中获得了精度增益。
第二,与普通的对应网络相比,34层ResNet使Top-1误差减少了3.5%(表2),这是成功地减少了训练误差(图2)的结果(图4右 VS 左))。这一比较验证了残差学习在极深系统上的有效性。
最后,我们还注意到,18层普通/残差网具有大致相等的精确率(表2),但18层ResNet的收敛速度更快(图4右 VS 左)。当网络“不太深”(比如这里的18层)时,当前的SGD解决程序仍然能够为普通网络找到好的解决方案。在这种情况下,ResNet通过在早期阶段提供更快的收敛速度来简化优化。
恒等快捷键 VS 投影快捷键( Projection Shortcuts)。我们已经证明,无参数的恒等快捷键有助于培训。接下来我们研究投影快捷键(eqn.(2)。在表3中,我们比较了三个选项:(A)零填充快捷键用于增加维度,所有快捷方式都是无参数的(与表2和图4右相同);(B)投影快捷键用于增加尺寸,而其他快捷键是恒等快捷键;(C)所有快捷键都是投影快捷键。
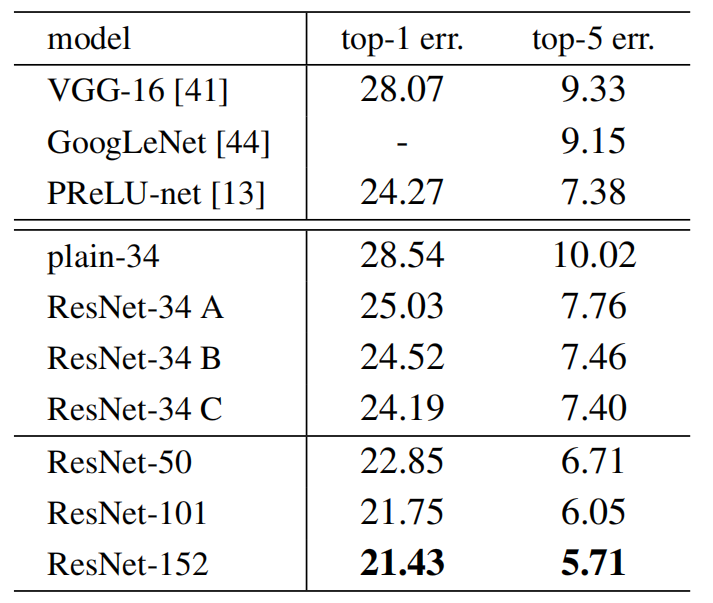
表3、对ImageNet验证的错误率(%,10-crop测试)。vgg-16是基于我们的测试。ResNet-50/101/152属于方案B ,它只对增加的维度使用投影(快捷键)。
表3显示,所有这三个选项都比普通的对应方案要好得多。B比A稍好。我们认为,这是因为A中零填充的维度实际上并没有(使用)残差学习。C比b略好,我们把这归因于许多(13个)投影快捷键引入的额外参数。但是a/b/c之间的小差异表明,投影快捷键对于解决退化问题并不重要。因此,在本文的其余部分中,我们不使用选项c以降低计算/时间复杂度和模型大小。恒等快捷键对于不增加下面介绍的瓶颈架构(bottleneck architectures)的复杂性特别重要。
更深层次的瓶颈架构。接下来,我们将描述我们针对ImageNet的更深层次的网络。由于考虑到我们负担得起的训练时间,我们将积木块(building block)修改为瓶颈设计(bottleneck design)。对于每个残差函数F,我们使用一个由3层组成的堆栈,而不是2层(图5)。这三层分别是1×1、3×3和1×1卷积,其中1×1层负责减小然后增加(恢复)维数,使3×3层成为输入/输出维数较小的瓶颈。图5给出了一个例子,其中两种设计都具有相似的时间复杂度。
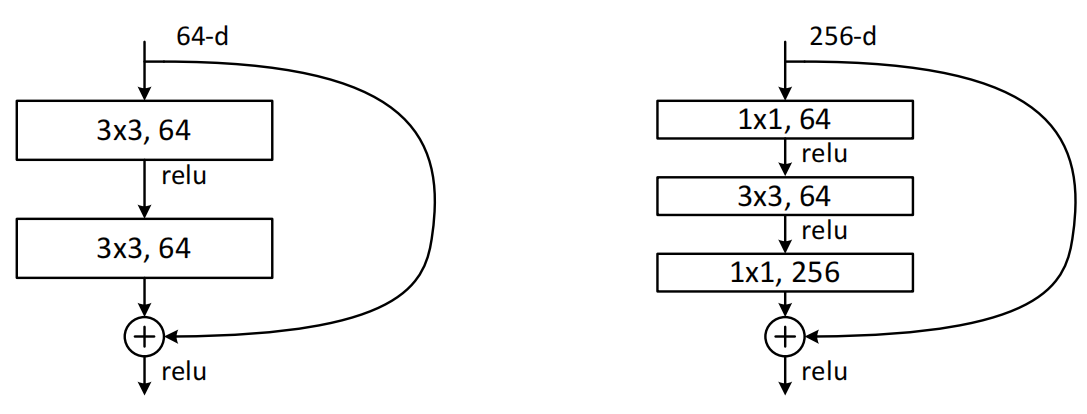
图5、ImageNet的一个更深层次的残差函数F。左图:如图3所示的用于ResNet-34的一个及积木块(在56×56特征图上)。右:ResNet-50/101/152的“瓶颈”积木块。
无参数的恒等快捷键对于瓶颈架构尤其重要。如果是图5(右)中的同恒等快捷键用投影快捷键代替,可以看出时间复杂度和模型大小加倍,因为快捷方式连接到两个高维端点。因此,恒等快捷键为瓶颈设计提供了更有效的模型。
50层ResNet:我们将34层网络中的每个2层块替换为这个3层瓶颈块,从而形成一个50层ResNet(表1).我们使用选项B来增加维度。这种模式有38亿次FLOPs。
101层和152层 ResNet:我们使用更多的三层块来构造101层和152层的ResNet(表1).值得注意的是,虽然深度明显增加,但152层 ResNet((113亿次 FLOPs)的复杂性仍然低于vgg-16/19网(153/196亿次 FLOPs)。
50/101/152层ResNet比34层网有相当大程度的准确率提升(表3和表4)。我们没有观察到退化的问题,因此,我们可以享受从大大增加的深度中获得的显著的精确性。所有评价指标都能看到深度的好处(表3和表4)。
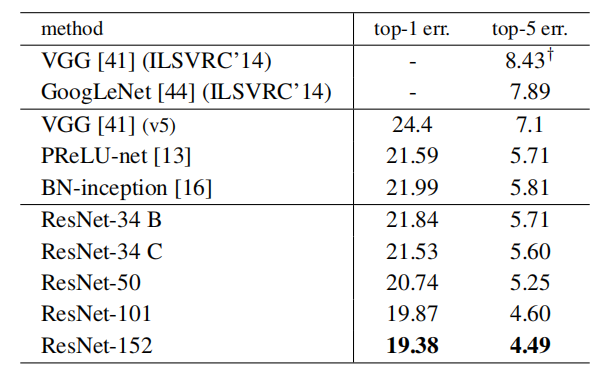
表4、ImageNet验证集上单模型结果的错误率(%)(除了†报告了测试集)。
和最先进的方法比较。在表4中,我们将与之前最好的单模型结果进行比较。我们的基线34层ResNet已经达到了非常竞争的准确性。我们的152层 ResNet的单模型Top-5验证误差为4.49%。这个单一模型的结果优于所有以前的集成结果(表5)。我们将六个不同深度的模型组合成一个整体(在提交时只有两个152层网络)。这将得到了测试集上3.57%的Top-5错误(表5).这一项目获得了2015年ILSVRC的第一名。
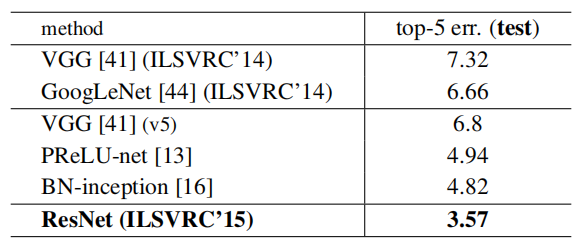
表5、组合的错误率(%)。在ImageNet的测试集上的top-5错误,并由测试服务器报告。
4.2 CIFAR-10和分析
我们在CIFAR-10数据集[20]进行了更多的研究,该数据集包括50个训练图像和10个类别的10k测试图像。我们在训练集上进行了实验训练,并在测试集上进行了评估。我们的重点是极深网络的行为,而不是推进最先进的结果,所以我们故意使用简单的架构如下。
普通/残差结构遵循图3(中/右)中的形式。网络输入32×32图像,每像素被减去每像素平均( with the per-pixel mean subtracted)。第一层为3×3卷积层。然后,我们在尺寸为{32,16,8}的特征映射上分别使用3×3卷积的共6n层叠加,每个特征地图大小都有2n层。滤波数分别为{16,32,64}。下采样是以2的步长的卷积来执行的。。网络以全局平均池、10路全连接层和softmax为结束。共有6n+2层加权层。下表概述了该体系结构:

当使用快捷连接时,它们被连接到3×3层的对上(总共3n条捷径)。在这个数据集中,我们在所有情况下都使用恒等快捷键(即选项A),因此,我们的残差模型的深度、宽度和参数与对应的普通模型完全相同。
我们使用权重衰减为0.0001,动量为0.9,采用了在[13]中的权值初始化在[13]和bn[16],但没有使用Dropout。这些模型是在两个GPU上训练的,小批量大小为128。我们的学习速度为0.1,在第32K和48K次迭代时除以10,在64k迭代时终止训练,这是由45k/5k训练/验证的分割决定。我们按照[24]中的简单数据增强进行训练:每边填充4个像素,从填充图像或水平翻转中随机抽取32×32帧。对于测试,我们只评估原始32×32图像的单一图像。
我们比较n={3,5,7,9},从而形成的20,32,44和56层网络。图6(左)显示了普通网的行为。深普通网随着深度增大,深度训练误差较大。这个现象类似于ImageNet(图4左)和mnist(见[42])上的现象,这表明这种优化困难是一个基本问题。
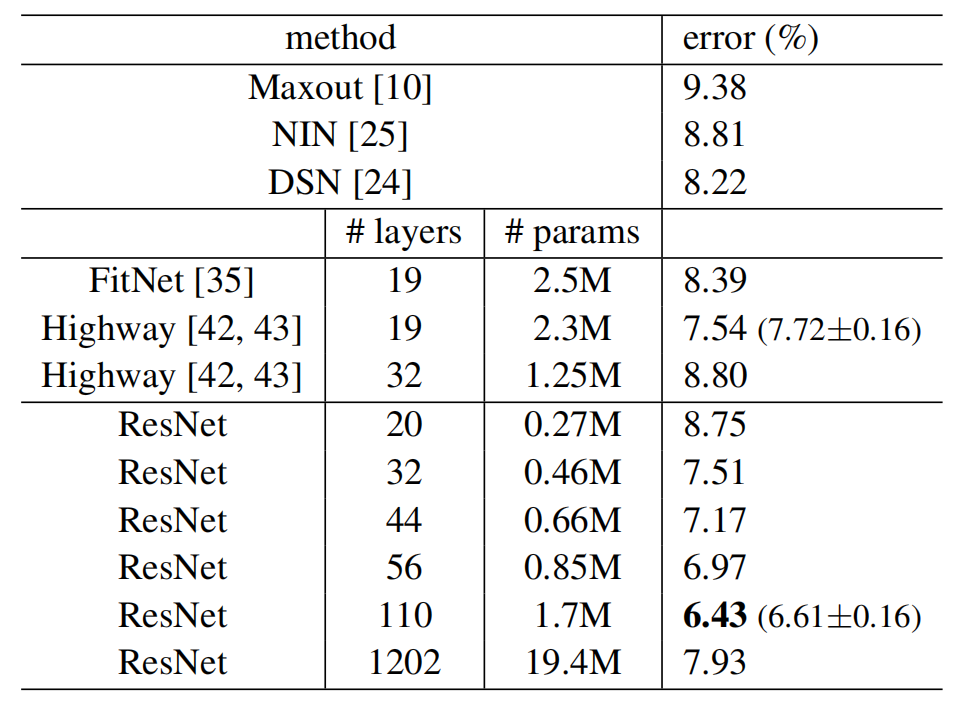
表6、CIFAR-10测试集的分类错误。所有方式都有数据增强。对于ResNet-110,我们运行5次,显示“最佳(平均±STD)”,如[43]中。
我们进一步探索了当n=18时获得的110层ResNet。在这种情况下,我们发现初始学习速率0.1太大,以致无法开始收敛。因此,我们使用0.01的学习速率为训练热身,直到训练误差小于80%(约400次迭代),然后将学习速率改为0.1继续训练。学习计划的其余部分和以前一样。这个110层网络能够很好地收敛(图6, 中)。它的参数比 FitNet[35]和 Highway[42](表6)等其他深而瘦的网络少,但却是最先进的结果之一(6.43%,表6)。
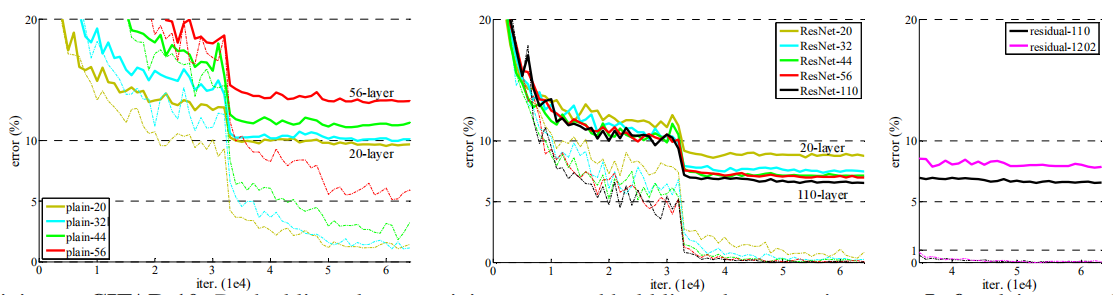
图6、在CIFAR-10上的训练。虚线表示训练错误,粗体线表示测试错误。左:普通网络。普通-110的误差大于60%,不显示。中间:残差网。右:有110层和1202层的残差网。
层响应分析。图7显示层响应的标准差(std)。响应为每个3×3层的输出,它在BN之后,在其它非线性(relu/加法)之前。对于ResNet,本分析揭示了残差函数的响应强度。图7表明残差网的响应一般比普通网的小。这些结果支持了我们的基本动机(第3.1节),即残差函数一般比非残差函数更接近于零。我们还注意到,较深的ResNet的响应幅度较小,如图7中ResNet-20、56和110之间的比较所示。当有更多的层时,单个的一层残差网倾向于对信号进行较少的修改。
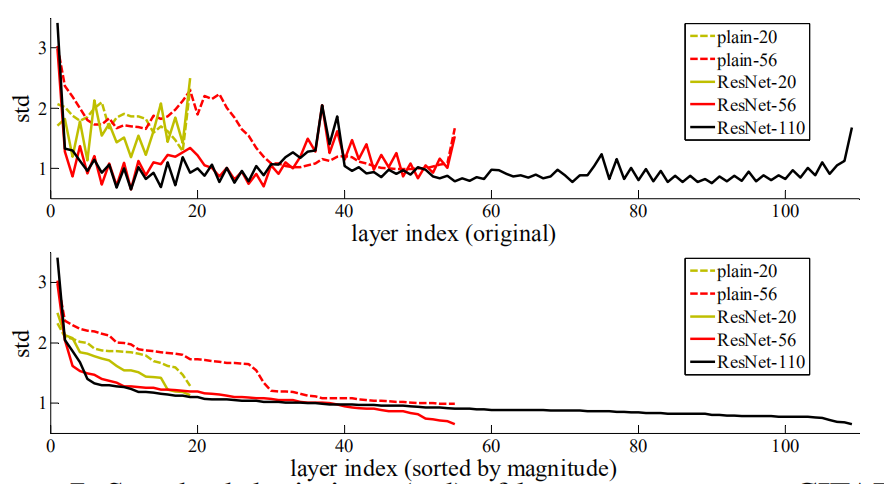
图7、CIFAR-10层响应的标准差(STD)。响应是每个3×3层的输出,在BN之后,在非线性之前。顶部:各层按原来的顺序显示。底部:响应按降序排列。
探索超过1000层(的网络)。我们探索了一个超过1000层的深度模型。我们设置n=200得到1202层网络,该网络就像上面所描述的那样被训练。我们的方法不存在优化困难,该1000层网络的训练误差小于0.1%(图6,右)。它的测试误差仍然相当好(7.93%,表6)。
但在这些激进的深层次模型上,仍存在一些有待解决的问题。这个1202层网络的测试结果比我们的110层网络差,尽管两者都有相似的训练误差。我们认为这是因为过拟合。对于这个小数据集,1202层网络可能不必要地大(19.4M)。在此数据集使用强正则化,如maxout[10]或dropout[14],可以获得最佳结果([10,25,24,35]。但在本文中,我们使用的是无 maxout/无漏的方法,只需通过深而瘦的结构设计来实现正则化,而不分散对优化的困难的关注。但是,与更强的正则化相结合可以提高结果,这是我们今后研究的方向。
4.3 在PASCAL和MS COCO上的目标检测
该方法对其它识别任务具有较好的泛化性能。表7和表8显示了PASCAL VOC 2007 and 2012[5]和COCO[26]的目标检测基线结果。我们采用Faster R-CNN[32]作为检测方法。在这里,我们对用ResNet-101替换VGG-16[41]的改进感兴趣。使用这两种模型的检测实现(见附录)是相同的,因此收益只能归功于更好的网络。最值得注意的是,在具有挑战性的coco数据集上,我们得到了coco标准度量的6.0%的增长(map@[.5,.95]),,这是一个28%的相对改进。这一收益完全归功于所学习的表述(learned representations)。
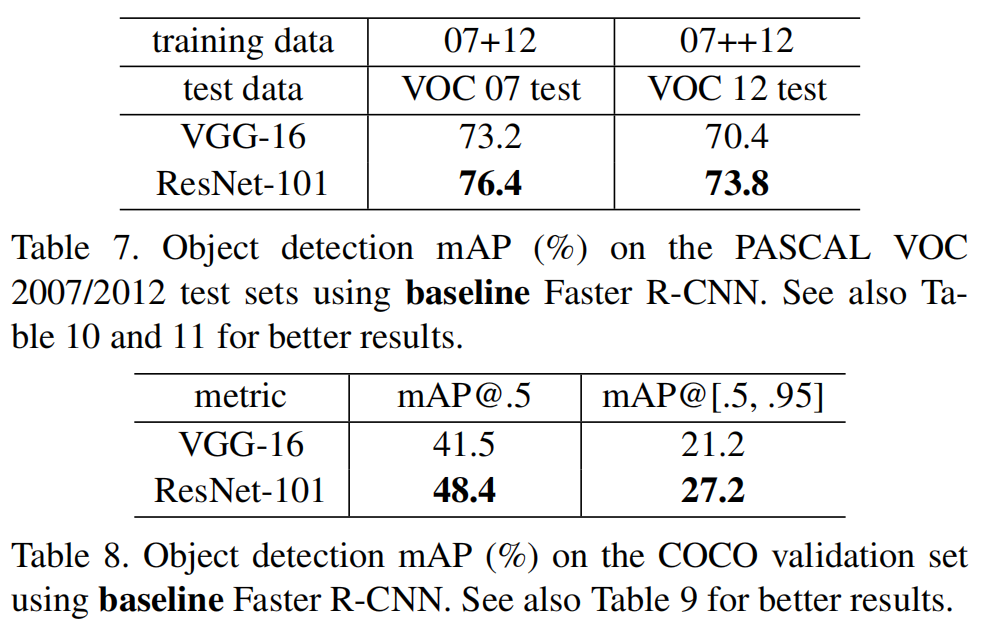
表7、在Pascal voc 2007/2012测试集上使用基线Faster R-CNN的目标检测 mAP(%)。更好的结果见10和11。
表8、在coco验证集上 使用基线Faster R-CNN的目标检测mAP(%)。另见表9,以获得更好的结果。
基于深度剩余网,我们在ILSVRC的几个项目中获得了第一名:Imagenet检测,ImageNet定位,coco检测和coco分割。详情见附录。
参考文献
[1] Y. Bengio, P. Simard, and P. Frasconi. Learning long-term dependencies with gradient descent is difficult. IEEE Transactions on NeuralNetworks, 5(2):157–166, 1994.
[2] C. M. Bishop. Neural networks for pattern recognition. Oxford university press, 1995.
[3] W. L. Briggs, S. F. McCormick, et al. A Multigrid Tutorial. Siam, 2000.
[4] K. Chatfield, V. Lempitsky, A. Vedaldi, and A. Zisserman. The devil is in the details: an evaluation of recent feature encoding methods. In BMVC, 2011.
[5] M. Everingham, L. Van Gool, C. K. Williams, J. Winn, and A. Zis-serman. The Pascal Visual Object Classes (VOC) Challenge. IJCV, pages 303–338, 2010.
[6] S. Gidaris and N. Komodakis. Object detection via a multi-region & semantic segmentation-aware cnn model. In ICCV, 2015.
[7] R. Girshick. Fast R-CNN. In ICCV, 2015.
[8] R. Girshick, J. Donahue, T. Darrell, and J. Malik. Rich feature hierarchies for accurate object detection and semantic segmentation. In CVPR, 2014.
[9] X. Glorot and Y. Bengio. Understanding the difficulty of training deep feedforward neural networks. In AISTATS, 2010.
[10] I. J. Goodfellow, D. Warde-Farley, M. Mirza, A. Courville, and Y. Bengio. Maxout networks. arXiv:1302.4389, 2013.
[11] K. He and J. Sun. Convolutional neural networks at constrained time cost. In CVPR, 2015.
[12] K. He, X. Zhang, S. Ren, and J. Sun. Spatial pyramid pooling in deep convolutional networks for visual recognition. In ECCV, 2014.
[13] K. He, X. Zhang, S. Ren, and J. Sun. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In ICCV, 2015.
[14] G. E. Hinton, N. Srivastava, A. Krizhevsky, I. Sutskever, and R. R. Salakhutdinov. Improving neural networks by preventing coadaptation of feature detectors. arXiv:1207.0580, 2012.
[15] S. Hochreiter and J. Schmidhuber. Long short-term memory. Neural computation, 9(8):1735–1780, 1997.
[16] S. Ioffe and C. Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In ICML, 2015.
[17] H. Jegou, M. Douze, and C. Schmid. Product quantization for nearest neighbor search. TPAMI, 33, 2011.
[18] H. Jegou, F. Perronnin, M. Douze, J. Sanchez, P. Perez, and C. Schmid. Aggregating local image descriptors into compact codes. TPAMI, 2012.
[19] Y. Jia, E. Shelhamer, J. Donahue, S. Karayev, J. Long, R. Girshick, S. Guadarrama, and T. Darrell. Caffe: Convolutional architecture for fast feature embedding. arXiv:1408.5093, 2014.
[20] A. Krizhevsky. Learning multiple layers of features from tiny images. Tech Report, 2009.
[21] A. Krizhevsky, I. Sutskever, and G. Hinton. Imagenet classification with deep convolutional neural networks. In NIPS, 2012.
[22] Y. LeCun, B. Boser, J. S. Denker, D. Henderson, R. E. Howard, W. Hubbard, and L. D. Jackel. Backpropagation applied to hand-written zip code recognition. Neural computation, 1989.
[23] Y.LeCun, L.Bottou, G.B.Orr, andK.-R.Müller. Efficientbackprop. In Neural Networks: Tricks of the Trade, pages 9–50. Springer, 1998.
[24] C.-Y. Lee, S. Xie, P. Gallagher, Z. Zhang, and Z. Tu. Deeply-supervised nets. arXiv:1409.5185, 2014.
[25] M. Lin, Q. Chen, and S. Yan. Network in network. arXiv:1312.4400, 2013.
[26] T.-Y. Lin, M. Maire, S. Belongie, J. Hays, P. Perona, D. Ramanan, P. Dollár, and C. L. Zitnick. Microsoft COCO: Common objects in context. In ECCV. 2014.
[27] J. Long, E. Shelhamer, and T. Darrell. Fully convolutional networks for semantic segmentation. In CVPR, 2015.
[28] G. Montúfar, R. Pascanu, K. Cho, and Y. Bengio. On the number of linear regions of deep neural networks. In NIPS, 2014.
[29] V. Nair and G. E. Hinton. Rectified linear units improve restricted boltzmann machines. In ICML, 2010.
[30] F. Perronnin and C. Dance. Fisher kernels on visual vocabularies for image categorization. In CVPR, 2007.
[31] T. Raiko, H. Valpola, and Y. LeCun. Deep learning made easier by linear transformations in perceptrons. In AISTATS, 2012.
[32] S. Ren, K. He, R. Girshick, and J. Sun. Faster R-CNN: Towards real-time object detection with region proposal networks. In NIPS, 2015.
[33] S. Ren, K. He, R. Girshick, X. Zhang, and J. Sun. Object detection networks on convolutional feature maps. arXiv:1504.06066, 2015.
[34] B. D. Ripley. Pattern recognition and neural networks. Cambridge university press, 1996.
[35] A. Romero, N. Ballas, S. E. Kahou, A. Chassang, C. Gatta, and Y. Bengio. Fitnets: Hints for thin deep nets. In ICLR, 2015.
[36] O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh, S. Ma, Z. Huang, A. Karpathy, A. Khosla, M. Bernstein, et al. Imagenet large scale visual recognition challenge. arXiv:1409.0575, 2014.
[37] A. M. Saxe, J. L. McClelland, and S. Ganguli. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks. arXiv:1312.6120, 2013.
[38] N. N. Schraudolph. Accelerated gradient descent by factor-centering decomposition. Technical report, 1998.
[39] N. N. Schraudolph. Centering neural network gradient factors. In Neural Networks: Tricks of the Trade, pages 207–226. Springer,1998.
[40] P. Sermanet, D. Eigen, X. Zhang, M. Mathieu, R. Fergus, and Y. Le- Cun. Overfeat: Integrated recognition, localization and detection using convolutional networks. In ICLR, 2014.
[41] K. Simonyan and A. Zisserman. Very deep convolutional networks for large-scale image recognition. In ICLR, 2015.
[42] R. K. Srivastava, K. Greff, and J. Schmidhuber. Highway networks. arXiv:1505.00387, 2015.
[43] R. K. Srivastava, K. Greff, and J. Schmidhuber. Training very deep networks. 1507.06228, 2015.
[44] C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke, and A. Rabinovich. Going deeper with convolutions. In CVPR, 2015.
[45] R. Szeliski. Fast surface interpolation using hierarchical basis functions. TPAMI, 1990.
[46] R. Szeliski. Locally adapted hierarchical basis preconditioning. In SIGGRAPH, 2006.
[47] T. Vatanen, T. Raiko, H. Valpola, and Y. LeCun. Pushing stochastic gradient towards second-order methods–backpropagation learning with transformations in nonlinearities. In Neural Information Processing, 2013.
[48] A. Vedaldi and B. Fulkerson. VLFeat: An open and portable library of computer vision algorithms, 2008.
[49] W. Venables and B. Ripley. Modern applied statistics with s-plus. 1999.
[50] M. D. Zeiler and R. Fergus. Visualizing and understanding convolutional neural networks. In ECCV, 2014.