一开始照着二维数组的逻辑去做,按照周围八个点的顺序遍历,居然 PA 也有 21 分... 后来自己找了好几个例子仍然没办法通过,这一看晴神的解析才发现这题是按三维数组去做的,而且遍历顺序是题目 Figure-1 的那 6 个点,emmm
三维数组大致如下( z 轴我只画了两层):
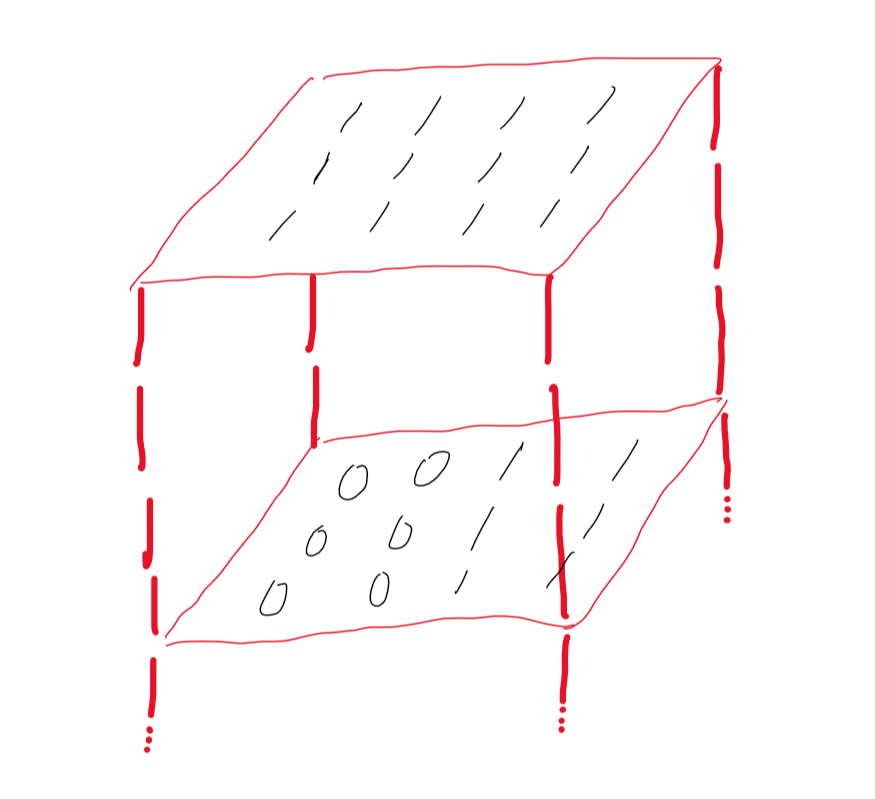
然后基本上套模板就行了,总的下来解 BFS() 主要是这三个方面:
/* 看到 BFS() 要想到 */ 1、晴神给的模板 2、坐标点的有效条件 3、什么样的坐标点才算是 "附近的点"
对于这道题,这样填充套模板:
/* 1、晴神给的模板 */
int bfs(起点s) { /* 起点入队 */ queue<node_t> q; q.push(s); inq[坐标点] = true; while (!q.empty()) { /* 访问队头,然后出队 */ node_t top = q.front(); q.pop(); /* bfs() 遍历 */ for (遍历 top 周围) { if (这个坐标点有效) { 入队(这个坐标点); inq[这个坐标点] = true; } } } }
(由于这道题要数点,所以后面要稍微改改,需要在 BFS() 的同时记录遍历到的 "有效" 点的数量)
模板中主要关注两处:1) for() 循环条件:"遍历 top 周围";2) for() 循环里面的 if() 的条件:"坐标点有效":
/* 2、坐标点的有效条件 */ bool isValid(坐标点的各维度坐标..) { if (越界) return false; if (该坐标点等于 0 || 该坐标点入队过) return false; return true; } /* 3、什么样的坐标点才算是 "附近的点" */ 这道题是六个方位:左、右、前、后、上、下
根据这些逻辑填充好模板就 ojbk