參考資料:https://www.cnblogs.com/TheRoadToTheGold/p/6254255.html
作者:xxy
感謝GAY神仙的講解和毒瘤代碼資瓷以及HMR神仙的優美的代碼
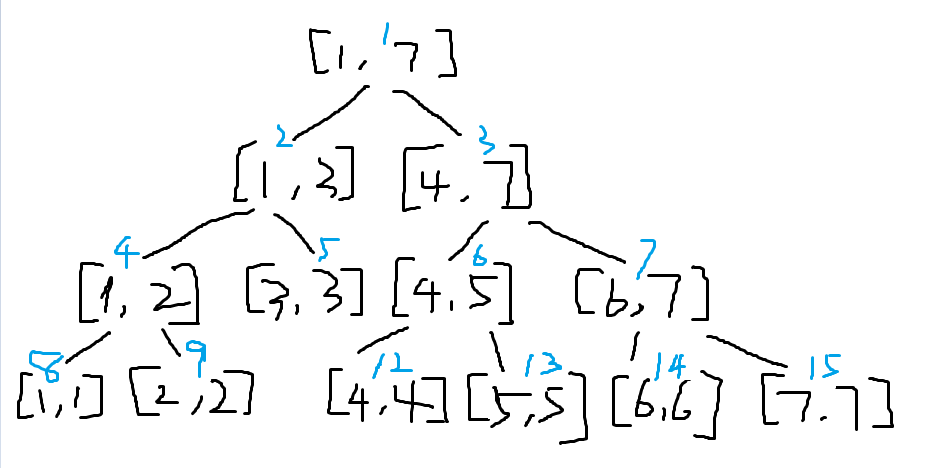
由此圖可知,每個區間左兒子包含區間[l,mid],右兒子包含區間[mid+1,r] 節點k的左兒子是(k<<1),右兒子是(k<<1+1)
而且兩倍空間明顯不夠用,所以開四倍就好了,我也不知道為什麼_(:з」∠)_據說可以畫個[1,10]的圖試試看。
1、建樹
二分需要修改的區間,如果有兒子就遞歸繼續修改,如果沒有就合併自己的兒子。
void build(int k,int ll,int rr){
tree[k].l=ll,tree[k].r=rr;
if(tree[k].l==tree[k].r){
tree[k].w=f[ll];
return ;
}
int m=((ll+rr)>>1),lls=(k<<1),rrs=((k<<1)|1);
build(lls,ll,m),build(rrs,m+1,rr);
tree[k].w=tree[lls].w+tree[rrs].w;
}
2·3、單點修改 單點查詢
先二分找到需要修改的點,然後往上一層一層地修改/查詢。
void cpoint(int k){
if(tree[k].l==tree[k].r){
tree[k].w+=z;
return ;
}
if(tree[k].lz) down(k);
int m=((tree[k].l+tree[k].r)>>1),lls=(k<<1),rrs=((k<<1)|1);
if(x<=m) cpoint(lls);
else cpoint(rrs);
tree[k].w=tree[lls].w+tree[rrs].w;
}
void apoint(int k){
if(tree[k].l==tree[k].r){
ans=tree[k].w;
return ;
}
if(tree[k].lz) down(k);
int m=((tree[k].l+tree[k].r)>>1);
if(x<=m) apoint((k<<1));
else apoint((k<<1)+1);
}
4·5、區間修改 區間查詢
二分找到需要修改/查詢的區間或子區間,再依次向上修改/查詢更大的區間。
void cinterval(int k){
if(tree[k].l>=x&&tree[k].r<=y){
tree[k].w+=(tree[k].r-tree[k].l+1)*z;
tree[k].lz+=z;
return ;
}
if(tree[k].lz) down(k);
int m=((tree[k].l+tree[k].r)>>1),lls=(k<<1),rrs=((k<<1)|1);
if(x<=m) cinterval(lls);
if(y>m) cinterval(rrs);
tree[k].w=tree[lls].w+tree[rrs].w;
}
void ainterval(int k){
if(tree[k].l>=x&&tree[k].r<=y){
ans+=tree[k].w;
return ;
}
if(tree[k].lz) down(k);
int m=((tree[k].l+tree[k].r)>>1);
if(x<=m) ainterval((k<<1));
if(y>m) ainterval((k<<1)+1);
}
以上是線段樹的基本操作。
//當然單點修改也可以用區間修改的函數啦,只要把左右端點設成一樣的就好了。
為了節約時間,我們引入Lazy標記——給每個節點打標記,需要用到該區間時再下放標記。即“修改的時候只修改對查詢有用的點”。
所以每次修改/查詢的時候,都要先下放標記再進行其他操作。
這個模板的修改都只是加法的,由加法結合率可知,這裡的標記可以保存很久再下放。
如果同時進行加法和乘法的修改,開兩個標記就好啦,不過乘法的標記要優先下放/否則會對以後的加法造成影響qwq。
·下傳標記
每次修改/查詢的時候都要檢查當前區間有無標記(如果標記只有加法,什麼時候下放都可以;如果有乘法,那麼當前區間就會對後面區間造成影響,所以這種標記最多只能存一次),如果有就下放——把當前標記下放給自己的兩個兒子,修改兒子的值,再把當前的標記清零(防止重複計算)。
void down(int k){
int lls=(k<<1),rrs=((k<<1)|1);
tree[lls].lz+=tree[k].lz,tree[rrs].lz+=tree[k].lz;
tree[lls].w+=tree[k].lz*(tree[lls].r-tree[lls].l+1);
tree[rrs].w+=tree[k].lz*(tree[rrs].r-tree[rrs].l+1);
tree[k].lz=0;
}
大概就是這樣,以下是Luogu【P3372】【模板】線段樹1 的代碼//當然有很大一部分與本題無關qwq
题目描述
如题,已知一个数列,你需要进行下面两种操作:
1.将某区间每一个数加上x
2.求出某区间每一个数的和
输入输出格式
输入格式:
第一行包含两个整数N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数,表示一个操作,具体如下:
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数加上k
操作2: 格式:2 x y 含义:输出区间[x,y]内每个数的和
输出格式:
输出包含若干行整数,即为所有操作2的结果。
#include<cctype>
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
inline long long read(){
long long a=0; int f=0; char c=getchar();
while(c<'0'||c>'9') { f|=c=='-'; c=getchar(); }
while(c>='0'&&c<='9') { a=(a<<3)+(a<<1)+(c^48); c=getchar(); }
return f? -a:a;
}
int n,m,x,y,z,a,f[100001];
long long ans;
struct qwq{ int l,r,lz; long long w; } tree[400004];
void build(int k,int ll,int rr){//建树
tree[k].l=ll,tree[k].r=rr;
if(tree[k].l==tree[k].r){
tree[k].w=f[ll];
return ;
}
int m=((ll+rr)>>1),lls=(k<<1),rrs=((k<<1)|1);
build(lls,ll,m),build(rrs,m+1,rr);
tree[k].w=tree[lls].w+tree[rrs].w;
}
void down(int k){//下传lazy标记
int lls=(k<<1),rrs=((k<<1)|1);
tree[lls].lz+=tree[k].lz,tree[rrs].lz+=tree[k].lz;
tree[lls].w+=tree[k].lz*(tree[lls].r-tree[lls].l+1);
tree[rrs].w+=tree[k].lz*(tree[rrs].r-tree[rrs].l+1);
tree[k].lz=0;
}
void cinterval(int k){//区间修改
if(tree[k].l>=x&&tree[k].r<=y){
tree[k].w+=(tree[k].r-tree[k].l+1)*z;
tree[k].lz+=z;
return ;
}
if(tree[k].lz) down(k);
int m=((tree[k].l+tree[k].r)>>1),lls=(k<<1),rrs=((k<<1)|1);
if(x<=m) cinterval(lls);
if(y>m) cinterval(rrs);
tree[k].w=tree[lls].w+tree[rrs].w;
}
void ainterval(int k){//区间查询
if(tree[k].l>=x&&tree[k].r<=y){
ans+=tree[k].w;
return ;
}
if(tree[k].lz) down(k);
int m=((tree[k].l+tree[k].r)>>1);
if(x<=m) ainterval((k<<1));
if(y>m) ainterval((k<<1)+1);
}
void cpoint(int k){//单点修改
if(tree[k].l==tree[k].r){
tree[k].w+=z;
return ;
}
if(tree[k].lz) down(k);
int m=((tree[k].l+tree[k].r)>>1),lls=(k<<1),rrs=((k<<1)|1);
if(x<=m) cpoint(lls);
else cpoint(rrs);
tree[k].w=tree[lls].w+tree[rrs].w;
}
void apoint(int k){//单点查询
if(tree[k].l==tree[k].r){
ans=tree[k].w;
return ;
}
if(tree[k].lz) down(k);
int m=((tree[k].l+tree[k].r)>>1);
if(x<=m) apoint((k<<1));
else apoint((k<<1)+1);
}
int main(){
n=read(),m=read();
for(int i=1;i<=n;++i) f[i]=read();
build(1,1,n);
for(int i=1;i<=m;++i){
a=read(),x=read(),y=read();
if(a==1) z=read(),cinterval(1);
else{
ans=0,ainterval(1);
printf("%lld
",ans);
}
}
return 0;
}
//HMR同學的據說是最好看的版本qwq
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cctype>
#define ll long long
#define gc getchar
#define maxn 100005
using namespace std;
inline ll read(){
ll a=0;int f=0;char p=gc();
while(!isdigit(p)){f|=p=='-';p=gc();}
while(isdigit(p)){a=(a<<3)+(a<<1)+(p^48);p=gc();}
return f?-a:a;
}int n,m;
ll a[maxn];
struct ahaha{
ll v,lz;
}t[maxn<<2];
#define lc p<<1
#define rc p<<1|1
inline void pushup(int p){
t[p].v=t[lc].v+t[rc].v;
}
inline void pushdown(int p,int l,int r){
int m=l+r>>1;ll &lz=t[p].lz;
t[lc].v+=lz*(m-l+1);t[lc].lz+=lz;
t[rc].v+=lz*(r-m);t[rc].lz+=lz;
lz=0;
}
void build(int p,int l,int r){
if(l==r){t[p].v=a[l];return;}
int m=l+r>>1;
build(lc,l,m);build(rc,m+1,r);
pushup(p);
}
void update(int p,int l,int r,int L,int R,ll z){
if(l>R||r<L)return;
if(L<=l&&r<=R){t[p].v+=z*(r-l+1);t[p].lz+=z;return;}
int m=l+r>>1;if(t[p].lz)pushdown(p,l,r);
update(lc,l,m,L,R,z);update(rc,m+1,r,L,R,z);
pushup(p);
}
ll query(int p,int l,int r,int L,int R){
if(l>R||r<L)return 0;
if(L<=l&&r<=R)return t[p].v;
int m=l+r>>1;if(t[p].lz)pushdown(p,l,r);
return query(lc,l,m,L,R)+query(rc,m+1,r,L,R);
}
inline void solve_1(){
int x=read(),y=read();ll z=read();
update(1,1,n,x,y,z);
}
inline void solve_2(){
int x=read(),y=read();
printf("%lld
",query(1,1,n,x,y));
}
int main(){
n=read();m=read();
for(int i=1;i<=n;++i)
a[i]=read();
build(1,1,n);
while(m--){
int zz=read();
switch(zz){
case 1:solve_1();break;
case 2:solve_2();break;
}
}
return 0;
}
Luogu【P3373】 【模板】線段樹2
题目描述
如题,已知一个数列,你需要进行下面三种操作:
1.将某区间每一个数乘上x
2.将某区间每一个数加上x
3.求出某区间每一个数的和
输入输出格式
输入格式:
第一行包含三个整数N、M、P,分别表示该数列数字的个数、操作的总个数和模数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数,表示一个操作,具体如下:
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数乘上k
操作2: 格式:2 x y k 含义:将区间[x,y]内每个数加上k
操作3: 格式:3 x y 含义:输出区间[x,y]内每个数的和对P取模所得的结果
输出格式:
输出包含若干行整数,即为所有操作3的结果。
#include<cctype>
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
inline long long read(){
long long a=0; int f=0; char c=getchar();
while(c<'0'||c>'9') { f|=c=='-'; c=getchar(); }
while(c>='0'&&c<='9') { a=(a<<3)+(a<<1)+(c^48); c=getchar(); }
return f? -a:a;
}
int n,m,a,b,c,d;
long long ans,mod;
long long f[100001];
struct Tree{ int l,r; long long w,lz1,lz2; } tree[400004];
inline void build(int k,int ll,int rr){
tree[k].l=ll,tree[k].r=rr,tree[k].lz1=1;
if(ll==rr){
tree[k].w=f[ll];
return ;
}
int mid=((ll+rr)>>1);
build((k<<1),ll,mid),build((k<<1)+1,mid+1,rr);
tree[k].w=tree[(k<<1)].w+tree[(k<<1)+1].w;
}
inline void down(int k){
int ls=(k<<1),rs=((k<<1)|1);
tree[ls].w=(tree[ls].w*tree[k].lz1+(tree[ls].r-tree[ls].l+1)*tree[k].lz2)%mod;
tree[rs].w=(tree[rs].w*tree[k].lz1+(tree[rs].r-tree[rs].l+1)*tree[k].lz2)%mod;
tree[ls].lz1=(tree[ls].lz1*tree[k].lz1)%mod;
tree[rs].lz1=(tree[rs].lz1*tree[k].lz1)%mod;
tree[ls].lz2=(tree[ls].lz2*tree[k].lz1+tree[k].lz2)%mod;
tree[rs].lz2=(tree[rs].lz2*tree[k].lz1+tree[k].lz2)%mod;
tree[k].lz1=1,tree[k].lz2=0;
}
inline void ch1(int k){
if(tree[k].l>=b&&tree[k].r<=c){
tree[k].w=(tree[k].w*d)%mod;
tree[k].lz1=(tree[k].lz1*d)%mod,tree[k].lz2=(tree[k].lz2*d)%mod;
return ;
}
if(tree[k].lz1!=1||tree[k].lz2) down(k);
int mid=((tree[k].l+tree[k].r)>>1),lls=(k<<1),rrs=(lls|1);
if(b<=mid) ch1(lls);
if(c>mid) ch1(rrs);
tree[k].w=(tree[lls].w+tree[rrs].w)%mod;
}
inline void ch2(int k){
if(tree[k].l>=b&&tree[k].r<=c){
tree[k].w=(tree[k].w+(tree[k].r-tree[k].l+1)*d)%mod;
tree[k].lz2=(tree[k].lz2+d)%mod;
return ;
}
if(tree[k].lz1!=1||tree[k].lz2) down(k);
int mid=((tree[k].l+tree[k].r)>>1),lls=(k<<1),rrs=(lls|1);
if(b<=mid) ch2(lls);
if(c>mid) ch2(rrs);
tree[k].w=(tree[lls].w+tree[rrs].w)%mod;
}
inline void ask(int k){
if(tree[k].l>=b&&tree[k].r<=c){
ans=(ans+tree[k].w)%mod;
return ;
}
if(tree[k].lz1!=1||tree[k].lz2) down(k);
int mid=((tree[k].l+tree[k].r)>>1),lls=(k<<1),rrs=(lls|1);
if(b<=mid) ask(lls);
if(c>mid) ask(rrs);
}
int main(){
n=read(),m=read(),mod=read();
for(int i=1;i<=n;++i) f[i]=read()%mod;
build(1,1,n);
while(m--){
a=read(),b=read(),c=read();
if(a==1) d=read(),ch1(1);
else if(a==2) d=read(),ch2(1);
else ans=0,ask(1),printf("%lld
",ans);
}
return 0;
}
//HMR神仙的美麗的代碼!
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cctype>
#define ll long long
#define gc getchar
#define maxn 100005
using namespace std;
inline ll read(){
ll a=0;int f=0;char p=gc();
while(!isdigit(p)){f|=p=='-';p=gc();}
while(isdigit(p)){a=(a<<3)+(a<<1)+(p^48);p=gc();}
return f?-a:a;
}int n,m;
ll mo,a[maxn];
struct ahaha{
ll v,lz,mul;
ahaha(){
mul=1;
}
}t[maxn<<2];
#define lc p<<1
#define rc p<<1|1
inline void pushup(int p){
t[p].v=t[lc].v+t[rc].v;
}
inline void pushdown(int p,int l,int r){
int m=l+r>>1;ll &lz=t[p].lz,&mul=t[p].mul;
if(mul!=1){
t[lc].v=t[lc].v*mul%mo;t[rc].v=t[rc].v*mul%mo;
t[lc].mul=t[lc].mul*mul%mo;t[rc].mul=t[rc].mul*mul%mo;
t[lc].lz=t[lc].lz*mul%mo;t[rc].lz=t[rc].lz*mul%mo;
mul=1;
}
if(lz){
t[lc].v=(t[lc].v+lz*(m-l+1))%mo;t[lc].lz=(t[lc].lz+lz)%mo;
t[rc].v=(t[rc].v+lz*(r-m))%mo;t[rc].lz=(t[rc].lz+lz)%mo;
lz=0;
}
}
void build(int p,int l,int r){
if(l==r){t[p].v=a[l];return;}
int m=l+r>>1;
build(lc,l,m);build(rc,m+1,r);
pushup(p);
}
void update1(int p,int l,int r,int L,int R,ll z){
if(l>R||r<L)return;
if(L<=l&&r<=R){
t[p].v=t[p].v*z%mo;
t[p].mul=t[p].mul*z%mo;
t[p].lz=t[p].lz*z%mo;
return;
}
int m=l+r>>1;if(t[p].mul!=1||t[p].lz)pushdown(p,l,r);
update1(lc,l,m,L,R,z);update1(rc,m+1,r,L,R,z);
pushup(p);
}
void update2(int p,int l,int r,int L,int R,ll z){
if(l>R||r<L)return;
if(L<=l&&r<=R){
t[p].v=(t[p].v+(r-l+1)*z%mo)%mo;
t[p].lz=(t[p].lz+z)%mo;
return;
}
int m=l+r>>1;if(t[p].mul!=1||t[p].lz)pushdown(p,l,r);
update2(lc,l,m,L,R,z);update2(rc,m+1,r,L,R,z);
pushup(p);
}
ll query(int p,int l,int r,int L,int R){
if(l>R||r<L)return 0;
if(L<=l&&r<=R)return t[p].v;
int m=l+r>>1;if(t[p].mul!=1||t[p].lz)pushdown(p,l,r);
return (query(lc,l,m,L,R)+query(rc,m+1,r,L,R))%mo;
}
inline void solve_1(){
int x=read(),y=read();ll z=read()%mo;
update1(1,1,n,x,y,z);
}
inline void solve_2(){
int x=read(),y=read();ll z=read()%mo;
update2(1,1,n,x,y,z);
}
inline void solve_3(){
int x=read(),y=read();
printf("%lld
",query(1,1,n,x,y));
}
int main(){
n=read();m=read();mo=read();
for(int i=1;i<=n;++i)
a[i]=read();
build(1,1,n);
while(m--){
int zz=read();
switch(zz){
case 1:solve_1();break;
case 2:solve_2();break;
case 3:solve_3();break;
}
}
return 0;
}
Q:如果當前訪問的區間不是要修改/查詢的區間,為什麼要下放標記呢?
A:因為要修改/查詢的區間可能是當前區間的子區間,所以如果不下放標記,該區間的子區間的Lazy標記就可能是錯的。