回溯搜索（数独）

这是我以前写的，现在转存在博客上

玩家需要根据9×9盘面上的已知数字，推理出所有剩余空格的数字，并满足每一行、每一列、每一个粗线宫（3×3）内的数字均含1-9，不重复。

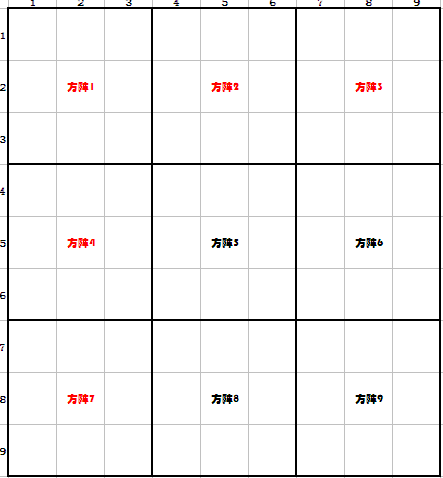
给出格子的行和列我们可以确定格子在哪一个宫

void cell(int x,int y)
{
     return x / 3 * 3 + y / 3;
}

我们只需要枚举其余所有的点

for(int map[][]=1;map[][]<10;map[][]++){
    if(check()){                              //每一层的check()是为了减少搜索次数的
        for(int map[][]=1;map[][]<10;map[][]++){  
            if(check()){
                for(int map[][]=1;map[][]<10;map[][]++){
                    if(check()){                          
                        ....                  //可以用递归实现 
                        ....                  //
                    }
                }
            }
        }
    }
}

这就是DFS，深度优先搜索

递归写法模板

//回溯法
void dfs(答案,搜索层数,其他参数){
    if(层数==maxdeep){
        更新答案;
        return;
    }
    (剪枝)
    for(枚举下一层可能的状态){ 
        if(check()){
              //更新全局变量表示状态的变量;
              //dfs(答案+新状态增加的价值,层数+1,其他参数);     
              //新状态必须是确定的，不能改变。
              //还原全局变量表示状态的变量;
        }
    }
}

构造标记数组

markrow[row][number];     //记录某一列是否存在某一个数字
markcol[col][number];        //记录某一行是否存在某一个数字
markbox[cell][number];      //记录某一宫是否存在某一个数字

这里需要注意深度搜索的顺序会很大程度的影响到算法的效率

代码

#include<iostream>
#include<algorithm>
#include<utility>
#include<cstdio>
#include<cstring>

using namespace std;

int map[9][9]; pair<int, int> Next[81];
int check = 0; // 已知的数的个数
int k = 0;  //递归的深度

int markrank[9][10];     //记录某一列是否存在某一个数字
int markrow[9][10];      //记录某一列是否存在某一个数字
int markcell[9][10];     //记录某一宫是否存在某一个数字

int cell(int x, int y)
{
      return x / 3 * 3 + y / 3;
}

// count函数用于记录(x,y)格子的还有几种可能情况
int count(int x, int y)
{
     int a[9] = { 0 }; int sum = 0;
     for (int i = 1; i <= 9; i++) {
         if (markrank[x][i] == 1 || markrow[y][i] == 1 || markcell[cell(x, y)][i] ==  1)
                a[i - 1] = 1;
      }
     for (int i = 0; i < 9; i++) {
          if (a[i] == 1) sum++;
     }
     return sum;
}

//next()函数的作用是求出当前可能情况最少的格子
pair<int, int> next() {
    pair<int, int> P2;
    int f = 0;
    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
              if (map[i][j] == 0 && f == 1) {
                   if (count(P2.first, P2.second) < count(i, j))
                    {
                        P2.first = i; P2.second = j;
                    }
               }
               else if (map[i][j] == 0 && f == 0) {
                    P2.first = i; P2.second = j;
                    f++;
               }
        }
    }
    return P2;
}


void dfs(int x, int y)
{
    if (k == 81 - check) {
         for (int i = 0; i < 9; i++) {
               for (int j = 0; j < 9; j++) {
                       cout << map[i][j] << " ";
               }
               cout << endl;
         }
     }
    else {
        for (int i = 1; i < 10; i++) {
             if (markrank[x][i]==0 && markrow[y][i]==0 && markcell[cell(x,y)][i]==0){
                 map[x][y] = i;
                 markcell[cell(x, y)][i] = 1; markrank[x][i] = 1;  markrow[y][i] = 1;
                 k++;
                 if (Next[k].first == -1) {
                     pair<int, int> P = next();
                     Next[k] = P;
                 }
                 dfs(Next[k].first, Next[k].second);
                 k--;
                 markcell[cell(x, y)][i] = 0; markrank[x][i] = 0;  markrow[y][i] = 0;
             }
        }
    }
}
int
main()
{
     memset(markrank, 0, sizeof(markrank));
      memset(markrow, 0, sizeof(markrow));
     memset(markcell, 0, sizeof(markcell));
      memset(Next, -1, sizeof(Next));
      for (int i = 0; i < 9; i++) {
          for (int j = 0; j < 9; j++) {
                  scanf("%d", &map[i][j]);
                  if (map[i][j] != 0) check++;
                  markcell[cell(i, j)][map[i][j]] = 1;
                  markrank[i][map[i][j]] = 1;
                  markrow[j][map[i][j]] = 1;
           }
      }
      pair<int, int> P = next();
      dfs(P.first, P.second);
      return 0;
}

解决数独的其他算法：dancing links 算法

号称世界上最难的数独

0 0 5 3 0 0 0 0 0
8 0 0 0 0 0 0 2 0
0 7 0 0 1 0 5 0 0
4 0 0 0 0 5 3 0 0
0 1 0 0 7 0 0 0 6
0 0 3 2 0 0 0 8 0
0 6 0 5 0 0 0 0 9
0 0 4 0 0 0 0 3 0
0 0 0 0 0 9 7 0 0