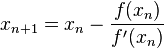Implement int sqrt(int x).
Compute and return the square root of x.
思路:二分查找法解决这道题
class Solution { public: int sqrt(int x) { if(x<=1) return x; int low=1; int high=x; while(low<=high) { int mid=low+(high-low)/2; if(mid==x/mid) return mid; else if(mid<x/mid) low=mid+1; else high=mid-1; } return high; } };
思路二:用牛顿求根法。首先,选择一个接近函数 零点的
零点的 ,计算相应的
,计算相应的 和切线斜率
和切线斜率 (这里
(这里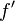 表示函数
表示函数 的导数)。然后我们计算穿过点
的导数)。然后我们计算穿过点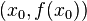 并且斜率为
并且斜率为 的直线和
的直线和 轴的交点的
轴的交点的 坐标,也就是求如下方程的解:
坐标,也就是求如下方程的解:
我们将新求得的点的 坐标命名为
坐标命名为 ,通常
,通常 会比
会比 更接近方程
更接近方程 的解。因此我们现在可以利用
的解。因此我们现在可以利用 开始下一轮迭代。迭代公式可化简为如下所示:
开始下一轮迭代。迭代公式可化简为如下所示:
已经证明,如果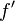 是连续的,并且待求的零点
是连续的,并且待求的零点 是孤立的,那么在零点
是孤立的,那么在零点 周围存在一个区域,只要初始值
周围存在一个区域,只要初始值 位于这个邻近区域内,那么牛顿法必定收敛。 并且,如果
位于这个邻近区域内,那么牛顿法必定收敛。 并且,如果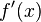 不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍。
不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍。
class Solution { public: int sqrt(int x) { if(x<=1) return x; double a=x; double b=0; while(abs(b-a)>1e-6) { b=a; a=(b+x/b)/2; } return (int)a; } };