待续.....
排序总结:
内排序:排序过程中,全部记录存放在内存中的排序。
总结:
一.排序稳定性:
稳定:冒泡排序,插入排序,归并,基数排序。
不稳定:选择,快速排序,希尔排序,堆排序。
二.平均时间复杂度
O(n2) :直接插入,简单选择,冒泡排序
在数据规模较小时(9w内),直接插入,简单选择排序差不多。
当数据较大时,冒泡排序算法的时间代价最高。
性能为O(n2)的算法基本上是相邻元素进行比较,基本上都是稳定的。
O(nlogn):快速,归并,希尔,堆排序。
其中,快速是最好的,其次是归并和希尔,堆排序在数据很大时效果明显。
三.排序算法的选择
1.数据规模较小:
(1)待排序列基本序的情况下,可以选择 直接插入排序;
(2)对稳定性不做要求,宜用插入或冒泡
2.数据规模不是很大
(1)完全可以用内存空间,序列杂乱无序,对稳定性没有要求,快速排序,此时要付出log(N)的额外空间
(2)序列本身可能有序,对稳定性有要求,空间允许下,宜用归并排序。
3.数据规模很大:
(1)对稳定性有求,则可考虑归并
(2)对稳定性无要求,宜用堆排序
4. 序列初始基本有序(正序),宜用直接插入 ,冒泡。
1.交换排序:冒泡排序和快速排序。
冒泡排序:
1.原理:
- 比较两个相邻的元素,将值大的元素交换到右端。
-
冒泡排序:
对待排序序列,从前向后依次比较相邻元素的排序码,若发现逆序则交换,使较大的元素逐渐从前面移到后面面,就像水底的气泡一样逐渐向上冒。
2、思想
- 依此比较相邻两个数,小的数放在前面,大的数放在后面
- 第一趟比较第1,2个数,小前大后;比较第2,3个数,小前大后,直至比较到把其中最大数放到最右端
- 第一趟之后,最后一个一定最大,比较第二趟,第二趟第一个不参与,把第二大的数放到倒数第二个位置
- 第二趟之后,倒数第二个数第二大,第三趟最后两个数不参与
- 依此类推,每一趟比较次数-1
public static void sort(int[] arr) {
for(int i=0;i<arr.length-1;i++)
for(int j=0;j<arr.length-1-i;j++) {
if(arr[j]>arr[j+1]) {
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1]=temp;
}
}
}
public static int[] sortV2(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
for (int j = i+1; j < arr.length; j++) {
if (arr[i] > arr[j]) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
}
return arr;
}
3、示例
- N个数字排序,进行 N-1趟排序
- 每趟排序次数为 N-i-1次
- 双重循环 外层控制趟数,内层控制每一趟排序次数
1.具体执行如下:
int[] arr = {6,3,8,2,9,1} 冒泡排序趟数和排序次数执行图:1.冒泡排序思想
冒泡排序就是比较两个相邻之间的数字,以升序排列为例。
以数组int[] a = {11,3,12,45,23} 为列。如果a[0]>a[1],交换二者的值,接着再用a[1]与a[2]比,如果需要交换就交换,不需要交换,再进行下一轮比较(a[2]与a[3]),直到最后a[a.length-2]与a[a.length-1]比较结束,此时第一轮比较已经结束,最大的值已经删选出来,并且已经放到了最后。
接着进行第二轮比较,第二轮比较的时候,数组从a[0]到a[a.length-2],到最后只剩下两个数字的时候,比较结束
2.代码实现与分析
//冒泡排序 两两之间比较(先把大的找出来)
private int[] bubbleSort(int[] a) {
for (int i = a.length - 1; i > 0; --i) {
//每一轮结束后,第二轮筛选的数就减少一个
for (int j = 0; j < i; j++) {
if (a[j] > a[j + 1]) {
//交换 把大的放后面 冒泡过程
int temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
}
}
}
return a;
}
冒泡排序的优化:
在排序过程中,如果一趟比较下来没有交换,说明是有序,因此在排序过程中要设置一个标志flag判断元素是否进行比较交换,减少不必要的比较。
Java实现冒泡排序(一)
原理:每次比较两个相邻的元素,将较大的元素交换至右端。
思路:每次冒泡排序操作都会将相邻的两个元素进行比较,看是否满足大小关系要求,如果不满足,就交换这两个相邻元素的次序,一次冒泡至少让一个元素移动到它应该排列的位置,重复N次,就完成了冒泡排序。
通过一个图来简单理解一下一次冒泡的过程:
经过一次冒泡,6这个当前数组中最大的元素飘到了最上面,如果进行N次这样操作,那么数组中所有元素也就到飘到了它本身该在的位置,就像水泡从水中飘上来,所以叫冒泡排序。
以上,第五第六次可以看到,其实第五次冒泡的时候,数组已经是有序的了,
因此,还可以优化,即如果当次冒泡操作没有数据交换时,那么就已经达到了有序状态
/**
* @description: 冒泡排序
* 冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求。
* 如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置,重复n 次,就完成了 n 个数据的排序工作
* **/
public class BubbleSort {
public void bubbleSort(Integer[] arr, int n) {
for (int i = 0; i < n; ++i) {
// 提前退出冒泡循环的标志位,即一次比较中没有交换任何元素,这个数组就已经是有序的了
boolean flag = false;
for (int j = 0; j < n - i - 1; ++j) { //此处你可能会疑问的j<n-i-1,因为冒泡是把每轮循环中较大的数飘到后面,
// 数组下标又是从0开始的,i下标后面已经排序的个数就得多减1,总结就是i增多少,j的循环位置减多少
if (arr[j] > arr[j + 1]) { //即这两个相邻的数是逆序的,交换
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
flag = true;
}
}
if (!flag) break;//没有数据交换,数组已经有序,退出排序
}
}
}
我自己在学习的过程中之前一直很纳闷第二层for循环里的j为啥要小于n-i-1,其实这个自己在纸上举个例子很快就明白了,如果上面代码里我的描述你还没有看懂,那么画一画。
时间复杂度:
如果我们的数据正序,只需要走一趟即可完成排序。所需的比较次数C和记录移动次数M均达到最小值,
即:Cmin=n-1;Mmin=0;所以,冒泡排序最好的时间复杂度为O(n)。
如果很不幸我们的数据是反序的,则需要进行n-1趟排序。每趟排序要进行n-i次比较(1≤i≤n-1),且每次比较都必须移动记录三次来达到交换记录位置。
在这种情况下,比较和移动次数均达到最大值:
即最坏情况下时间复杂度为O(n2) 【n的平方】; 所以,冒泡排序总的平均时间复杂度为:O(n2) 。
2.快速排序:
快速排序是对冒泡排序的改进。
定义
通过一趟排序将要排序的数据分给成独立的两部分,其中一部分的所有数据都要比另一部分的所有都要小,然后按照此方法对这两部分数据分别进行快速排序,整个排序过程递归进行。——自己概括,数组中定义一个值为轴值,比其大放一侧,比其小的放另一侧,因此化为两部分,再用递归的方式,直到全部变成有序数列。本质还是两两交换!
基本思想:
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部数据分别进行快速排序,整个排序过程可以进行递归排序,达到整个过程变成有序序列。
【总结】
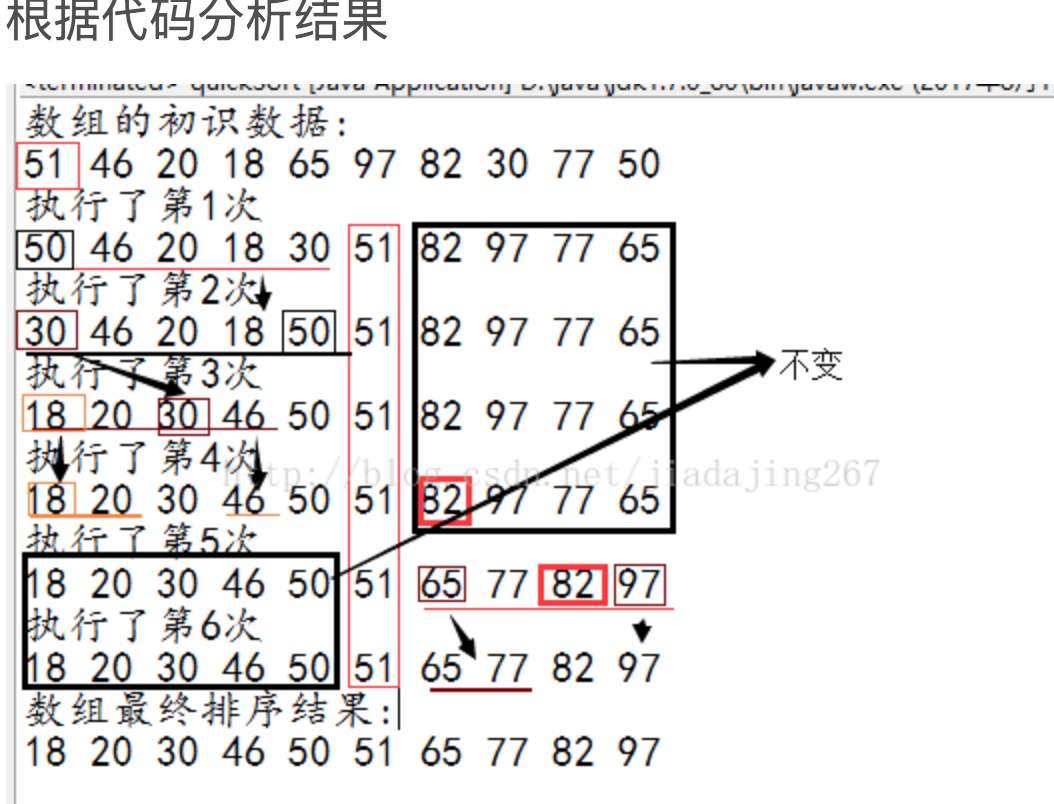
根据上述两种排序,发现两种算法都是采用两两交换的方式进行排序。而同样的数据冒泡用了9次,而快速用了6次。两者采用的方式相同,在执行效率上,快速排序算是冒泡排序的优化版。
public class quickSort {
private static int num = 0;
public static void main(String[] args) {
int[] a = {51, 46, 20, 18, 65, 97, 82, 30, 77, 50};
quick(a, 0, a.length - 1);
}
public static void quick(int[] list, int low, int high) {
if (list.length > 0 && low < high) {
int middle = getMiddle(list, low, high);
quick(list, low, middle - 1);
quick(list, middle + 1, high);
}
}
/**
* @param list 数组
* @param low 最小坐标
* @param high 最高位坐标
* @Description: 选取中间值
*/
public static int getMiddle(int[] list, int low, int high) {
//计算执行次数
num++;
int temp = list[low]; //选择第一个数作为轴值,存放于临时变量中
while (low < high) { //保证一致正序选择
//保证正序的前提下(从左到右),如果右侧大于轴值,则判断 右侧数据的下一个
while (low < high && list[high] > temp) {
high--;
}
//在右侧找到小于temp轴值的数,则进行交换
list[low] = list[high];
//保证正序的前提下(从左到右),如果左侧小于轴值,则判断左侧数据的下一个
while (low < high && list[low] <= temp) {
low++;
}
list[high] = list[low];//在左侧找到大于temp轴值的数,则进行交换
}
list[low] = temp;
System.out.println("执行了第" + num + "次");
for (int i = 0; i < list.length; i++) {
System.out.print(list[i] + " ");
}
System.out.println();
return low;
}
}