[zz]判断两矩形是否交叉（包括包含的情况）

问题：给定两个矩形A和B，矩形A的左上角坐标为（Xa1,Ya1），右下角坐标为（Xa2,Ya2），矩形B的左上角坐标为（Xb1,Yb1），右下角坐标为（Xb2,Yb2）。
（1）设计一个算法，确定两个矩形是否相交（即有重叠区域）
（2）如果两个矩形相交，设计一个算法，求出相交的区域矩形

(1)对于这个问题，一般的思路就是判断一个矩形的四个顶点是否在另一个矩形的区域内。这个思路最简单，但是效率不高，并且存在错误，错误在哪里，下面分析一下。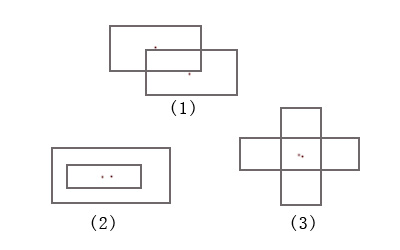
                   

如上图，把矩形的相交（区域重叠）分成三种（可能也有其他划分），对于第三种情况，如图中的（3），两个矩形相交，但并不存在一个矩形的顶点在另一个矩形内部。所以那种思路存在一个错误，对于这种情况的相交则检查不出。

仔细观察上图，想到另一种思路，那就是判断两个矩形的中心坐标的水平和垂直距离，只要这两个值满足某种条件就可以相交。
           矩形A的宽 Wa = Xa2-Xa1 高 Ha = Ya2-Ya1
           矩形B的宽 Wb = Xb2-Xb1 高 Hb = Yb2-Yb1
           矩形A的中心坐标 (Xa3,Ya3) = （ (Xa2+Xa1)/2 ，(Ya2+Ya1)/2 ）
           矩形B的中心坐标 (Xb3,Yb3) = （ (Xb2+Xb1)/2 ，(Yb2+Yb1)/2 ）
           所以只要同时满足下面两个式子，就可以说明两个矩形相交。

                 1） | Xb3-Xa3 | <= Wa/2 + Wb/2
                 2） | Yb3-Ya3 | <= Ha/2 + Hb/2
           即：
                   | Xb2+Xb1-Xa2-Xa1 | <= Xa2-Xa1 + Xb2-Xb1
                   | Yb2+Yb1-Ya2-Ya1 | <=Y a2-Ya1 + Yb2-Yb1

(2) 对于这个问题，假设两个矩形相交，设相交之后的矩形（？也可能是平行四边形，但是也满足这种情况）为C，且矩形C的左上角坐标为（Xc1,Yc1），右下角坐标为（Xc2,Yc2），经过观察上图，很显然可以得到：
            Xc1 = max(Xa1,Xb1)
            Yc1 = max(Ya1,Yb1)
   　　   Xc2 = min(Xa2,Xb2)
            Yc2 = min(Ya2,Yb2)
   这样就求出了矩形的相交区域。
     另外，注意到在不假设矩形相交的前提下，定义（Xc1,Yc1）,（Xc2,Yc2）,且Xc1,Yc1,Xc2,Yc2的值由上面四个式子得出。这样，可以依据Xc1,Yc1,Xc2,Yc2的值来判断矩形相交。
     Xc1,Yc1,Xc2,Yc2只要同时满足下面两个式子，就可以说明两个矩形相交。
              3) Xc1 <= Xc2
              4) Yc1 <= Yc2
    即：
             max(Xa1,Xb1) <= min(Xa2,Xb2)
             max(Ya1,Yb1) <= min(Ya2,Yb2)

 继续思考如下方法是否可行：

 方法一：

   如果两个矩形相交，则必然存在线条交叉，而能交叉的线条只有横线和竖线，两根横线或两根竖线都不可能交叉。所以，这个问题就转化成寻找是否存在交叉的横线与竖线。（横线重叠情况？）
　　另外，A线与B线交叉等价于B线与A线交叉，所以，只要写一个函数就足够用了，多调用几次，反正计算机是专门做简单而又烦琐的工作的。

　　下面是这个函数：判断一条横线和一条竖线是否交叉。该函数的参数分别是：横线左、横线右，横线Y，竖线上，竖线下，竖线X。

bool CrossLine(left, right, y, top, bottom, x)
{
　//判断一根横线和一根竖线是否交叉
　//横线有三个参数：left, right和y
　//竖线有三个参数：top, bottom和x
　return (top < y) && (bottom > y)&& (left < x) && (right > x);
}

　　下面是判断两个矩形是否相交的函数，把同一个函数多调用几篇就OK了。

bool CrossRect(CRect &r1, CRect &r2)
{
　//判断两个矩形是否相交，共8种，横竖交叉
　//从一个矩形中取出一条横线，与另一矩形中的一条竖线判断是否交叉
　return CrossLine(r1.x1, r1.x2, r1.y1, r2.y1, r2.y2, r2.x1)
　　　|| CrossLine(r1.x1, r1.x2, r1.y1, r2.y1, r2.y2, r2.x2)
　　　|| CrossLine(r1.x1, r1.x2, r1.y2, r2.y1, r2.y2, r2.x1)
　　　|| CrossLine(r1.x1, r1.x2, r1.y2, r2.y1, r2.y2, r2.x2)
　　　|| CrossLine(r2.x1, r2.x2, r2.y1, r1.y1, r1.y2, r1.x1)
　　　|| CrossLine(r2.x1, r2.x2, r2.y1, r1.y1, r1.y2, r1.x2)
　　　|| CrossLine(r2.x1, r2.x2, r2.y2, r1.y1, r1.y2, r1.x1)
　　　|| CrossLine(r2.x1, r2.x2, r2.y2, r1.y1, r1.y2, r1.x2);
}

 方法二：

matlab 具有强大的图形处理功能，它刚好有那么一个函数可以实现这个功能，那就是 rectint 。

   函数介绍：

     RECTINT 矩形相交函数。

     AREA = RECTINT(A,B) 返回的矩形相交部分的面积。

     A和B是按位置向量指定的矩形

     如果A和B各指定一个长方形，面积是一个标量。

     A和B也可以是矩阵，其中每行是一个位置向量。那么返回的AREA是一个矩阵，是提供的所有矩形与 由A 或 B指定的矩形相交部分的面积。也就是说，如果A指定的矩形 是M × 4和B为N × 4，然后AERA是一个m × n矩阵，在面积（P，Q）是由指定的矩形面积来自 P 行的 A 和 Q 行的 B ，

   注：位置向量是一个四元向量 [X，Y，宽度，高度]， 这个X和Y指定矩形左下方的那个顶点的坐标宽度和高度意思是分别沿x轴 和Y轴的大小。

         例：

>> axes('xlim',[0 10],'ylim',[0 10])
>> a = [1 1 2 2];
>> b = [3 4 5 6];
>> rectangle('position',a)
>> rectangle('position',b)
>> c = [1 1 3 3];
>> rectangle('position',c)
>> rectint(a,c)

ans =

     4

>> rectint(b,c)

ans =

     0

>> rectint(a,b)

ans =

     0

>> d = [a;b];
>> rectint(d,c)     % 矩阵的情况

ans =

     4
     0

>>

 感觉很好用， 嘎嘎。。。有时间的话，将 open rectint 来看看里面的代码机制，看它是怎么实现的。。。

方法三： 

【解题思路】
假定矩形是用一对点表达的(minx,miny)(maxx,   maxy)  
那么两个矩形rect1{(minx1,miny1)(maxx1,   maxy1)},       rect2{(minx2,miny2)(maxx2,   maxy2)}  
   
相交的结果一定是个矩形，构成这个相交矩形rect{(minx,miny)(maxx, maxy)}的点对坐标是：  
minx   =   max(minx1,   minx2)  
miny   =   max(miny1,   miny2)  
maxx   =   min(maxx1,   maxx2)  
maxy   =   min(maxy1,   maxy2)  
   
如果两个矩形不相交，那么计算得到的点对坐标必然满足  
minx   >   maxx  
或者  
miny   >   maxy  

判定是否相交，以及相交矩形是什么都可以用这个方法一体计算完成

【源代码】

bool CardRectManager::IsIntersect(RECT* pRect1, RECT* pRect2)
{
    int nMaxLeft = 0;
    int nMaxTop = 0;
    int nMinRight = 0;
    int nMinBottom = 0;
    
    // Get the max left.
    if (pRect1->left >= pRect2->left)
    {
        nMaxLeft = pRect1->left;
    }
    else
    {
        nMaxLeft = pRect2->left;
    }
    // Get the max top.
    if (pRect1->top >= pRect2->top)
    {
        nMaxTop = pRect1->top;
    }
    else
    {
        nMaxTop = pRect2->top;
    }
    // Get the min right.
    if (pRect1->right <= pRect2->right)
    {
        nMinRight = pRect1->right;
    }
    else
    {
        nMinRight = pRect2->right;
    }
    // Get the min bottom.
    if (pRect1->bottom <= pRect2->bottom)
    {
        nMinBottom = pRect1->bottom;
    }
    else
    {
        nMinBottom = pRect2->bottom;
    }
    // Judge whether intersects.
    if (nMaxLeft > nMinRight || nMaxTop > nMinBottom)
    {
        return false;
    }
    else
    {
        return true;
    }
}

工作需要，我只使用了判断两矩形是否交叉功能。

 -----------------------------------------------------------------------------------------------------------------------------------------

根据原文档，对应写了一个函数，用于判断两矩形是否交叉：

 private bool CheckCross(Rectangle r1, Rectangle r2)
        {
            PointF c1 = new PointF(r1.Left + r1.Width / 2.0f, r1.Top + r1.Height / 2.0f);
            PointF c2 = new PointF(r2.Left + r2.Width / 2.0f, r2.Top + r2.Height / 2.0f);

            return (Math.Abs(c1.X - c2.X) <= r1.Width / 2.0 + r2.Width / 2.0 && Math.Abs(c2.Y - c1.Y) <= r1.Height / 2.0 + r2.Height / 2.0);

        }

转自：http://blog.csdn.net/zyxlsh/article/details/5937191