描述
小Hi:今天我们来学习一个强大的字符串处理工具:后缀自动机(Suffix Automaton,简称SAM)。对于一个字符串S,它对应的后缀自动机是一个最小的确定有限状态自动机(DFA),接受且只接受S的后缀。
小Hi:比如对于字符串S="aabbabd",它的后缀自动机是:
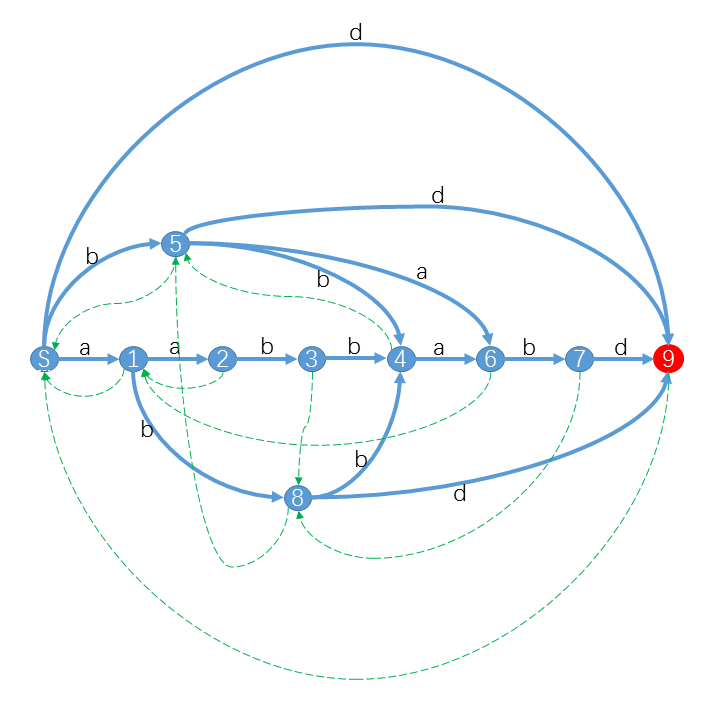
其中红色状态是终结状态。你可以发现对于S的后缀,我们都可以从S出发沿着字符标示的路径(蓝色实线)转移,最终到达终结状态。例如"bd"对应的路径是S59,"abd"对应的路径是S189,"abbabd"对应的路径是S184679。而对于不是S后缀的字符串,你会发现从S出发,最后会到达非终结状态或者“无路可走”。特别的,对于S的子串,最终会到达一个合法状态。例如"abba"路径是S1846,"bbab"路径是S5467。而对于其他不是S子串的字符串,最终会“无路可走”。 例如"aba"对应S18X,"aaba"对应S123X。(X表示没有转移匹配该字符)
小Ho:好像很厉害的样子!对于任意字符串都能构造出一个SAM吗?另外图中那些绿色虚线是什么?
小Hi:是的,任意字符串都能构造出一个SAM。我们知道SAM本质上是一个DFA,DFA可以用一个五元组 <字符集,状态集,转移函数、起始状态、终结状态集>来表示。下面我们将依次介绍对于一个给定的字符串S如何确定它对应的 状态集 和 转移函数 。至于那些绿色虚线虽然不是DFA的一部分,却是SAM的重要部分,有了这些链接SAM是如虎添翼,我们后面再细讲。
SAM的States
小Hi:这一节我们将介绍给定一个字符串S,如何确定S对应的SAM有哪些状态。首先我们先介绍一个概念 子串的结束位置集合 endpos。对于S的一个子串s,endpos(s) = s在S中所有出现的结束位置集合。还是以S="aabbabd"为例,endpos("ab") = {3, 6},因为"ab"一共出现了2次,结束位置分别是3和6。同理endpos("a") = {1, 2, 5}, endpos("abba") = {5}。
小Hi:我们把S的所有子串的endpos都求出来。如果两个子串的endpos相等,就把这两个子串归为一类。最终这些endpos的等价类就构成的SAM的状态集合。例如对于S="aabbabd":
| 状态 | 子串 | endpos |
|---|---|---|
| S | 空串 | {0,1,2,3,4,5,6} |
| 1 | a | {1,2,5} |
| 2 | aa | {2} |
| 3 | aab | {3} |
| 4 | aabb,abb,bb | {4} |
| 5 | b | {3,4,6} |
| 6 | aabba,abba,bba,ba | {5} |
| 7 | aabbab,abbab,bbab,bab | {6} |
| 8 | ab | {3,6} |
| 9 | aabbabd,abbabd,bbabd,babd,abd,bd,d | {7} |
小Ho:这些状态恰好就是上面SAM图中的状态。
小Hi:没错。此外,这些状态还有一些美妙的性质,且等我一一道来。首先对于S的两个子串s1和s2,不妨设length(s1) <= length(s2),那么 s1是s2的后缀当且仅当endpos(s1) ⊇ endpos(s2),s1不是s2的后缀当且仅当endpos(s1) ∩ endpos(s2) = ∅。
小Ho:我验证一下啊... 比如"ab"是"aabbab"的后缀,而endpos("ab")={3,6},endpos("aabbab")={6},是成立的。"b"是"ab"的后缀,endpos("b")={3,4,6}, endpos("ab")={3,6}也是成立的。"ab"不是"abb"的后缀,endpos("ab")={3,6},endpos("abb")={4},两者没有交集也是成立的。怎么证明呢?
小Hi:证明还是比较直观的。首先证明s1是s2的后缀=>endpos(s1) ⊇ endpos(s2):既然s1是s2后缀,所以每次s2出现时s1以必然伴随出现,所以有endpos(s1) ⊇ endpos(s2)。再证明endpos(s1) ⊇ endpos(s2)=>s1是s2的后缀:我们知道对于S的子串s2,endpos(s2)不会是空集,所以endpos(s1) ⊇ endpos(s2)=>存在结束位置x使得s1结束于x,并且s2也结束于x,又length(s1) <= length(s2),所以s1是s2的后缀。综上我们可知s1是s2的后缀当且仅当endpos(s1) ⊇ endpos(s2)。s1不是s2的后缀当且仅当endpos(s1) ∩ endpos(s2) = ∅是一个简单的推论,不再赘述。
小Ho:我好像对SAM的状态有一些认识了!我刚才看上面的表格就觉得SAM的一个状态里包含的子串好像有规律。考虑到SAM中的一个状态包含的子串都具有相同的endpos,那它们应该都互为后缀?
小Hi:你观察力还挺敏锐的。下面我们就来讲讲一个状态包含的子串究竟有什么关系。上文提到我们把S的所有子串按endpos分类,每一类就代表一个状态,所以我们可以认为一个状态包含了若干个子串。我们用substrings(st)表示状态st中包含的所有子串的集合,longest(st)表示st包含的最长的子串,shortest(st)表示st包含的最短的子串。例如对于状态7,substring(7)={aabbab,abbab,bbab,bab},longest(7)=aabbab,shortest(7)=bab。
小Hi:对于一个状态st,以及任意s∈substrings(st),都有s是longest(st)的后缀。证明比较容易,因为endpos(s)=endpos(longest(st)),所以endpos(s) ⊇ endpos(longest(st)),根据我们刚才证明的结论有s是longest(st)的后缀。
小Hi:此外,对于一个状态st,以及任意的longest(st)的后缀s,如果s的长度满足:length(shortest(st)) <= length(s) <= length(longsest(st)),那么s∈substrings(st)。 证明也是比较容易,因为:length(shortest(st)) <= length(s) <= length(longsest(st)),所以endpos(shortest(st)) ⊇ endpos(s) ⊇ endpos(longest(st)), 又endpos(shortest(st)) = endpos(longest(st)),所以endpos(shortest(st)) = endpos(s) = endpos(longest(st)),所以s∈substrings(st)。
小Ho:这么说来,substrings(st)包含的是longest(st)的一系列连续后缀?
小Hi:没错。比如你看状态7中包含的就是aabbab的长度分别是6,5,4,3的后缀;状态6包含的是aabba的长度分别是5,4,3,2的后缀。
SAM的Suffix Links
小Hi:前面我们讲到substrings(st)包含的是longest(st)的一系列连续后缀。这连续的后缀在某个地方会“断掉”。比如状态7,包含的子串依次是aabbab,abbab,bbab,bab。按照连续的规律下一个子串应该是"ab",但是"ab"没在状态7里,你能想到这是为什么么?
小Ho:aabbab,abbab,bbab,bab的endpos都是{6},下一个"ab"当然也在结束位置6出现过,但是"ab"还在结束位置3出现过,所以"ab"比aabbab,abbab,bbab,bab出现次数更多,于是就被分配到一个新的状态中了。
小Hi:没错,当longest(st)的某个后缀s在新的位置出现时,就会“断掉”,s会属于新的状态。比如上例中"ab"就属于状态8,endpos("ab"}={3,6}。当我们进一步考虑"ab"的下一个后缀"b"时,也会遇到相同的情况:"b"还在新的位置4出现过,所以endpos("b")={3,4,6},b属于状态5。在接下去处理"b"的后缀我们会遇到空串,endpos("")={0,1,2,3,4,5,6},状态是起始状态S。
小Hi:于是我们可以发现一条状态序列:7->8->5->S。这个序列的意义是longest(7)即aabbab的后缀依次在状态7、8、5、S中。我们用Suffix Link这一串状态链接起来,这条link就是上图中的绿色虚线。
小Ho:原来如此。
小Hi:Suffix Links后面会有妙用,我们暂且按下不表。
SAM的Transition Function
小Hi:最后我们来介绍SAM的转移函数。对于一个状态st,我们首先找到从它开始下一个遇到的字符可能是哪些。我们将st遇到的下一个字符集合记作next(st),有next(st) = {S[i+1] | i ∈ endpos(st)}。例如next(S)={S[1], S[2], S[3], S[4], S[5], S[6], S[7]}={a, b, d},next(8)={S[4], S[7]}={b, d}。
小Hi:对于一个状态st来说和一个next(st)中的字符c,你会发现substrings(st)中的所有子串后面接上一个字符c之后,新的子串仍然都属于同一个状态。比如对于状态4,next(4)={a},aabb,abb,bb后面接上字符a得到aabba,abba,bba,这些子串都属于状态6。
小Hi:所以我们对于一个状态st和一个字符c∈next(st),可以定义转移函数trans(st, c) = x | longest(st) + c ∈ substrings(x) 。换句话说,我们在longest(st)(随便哪个子串都会得到相同的结果)后面接上一个字符c得到一个新的子串s,找到包含s的状态x,那么trans(st, c)就等于x。
小Ho:吼~ 终于把SAM中各个部分搞明白了。
小Hi:SAM的构造有时空复杂度均为O(length(S))的算法,我们将在后面介绍。这一期你可以先用暴力算法依照定义构造SAM,先对SAM有个直观认识再说。
小Ho:没问题,暴力算法我最拿手了。我先写程序去了。
输入
第一行包含一个字符串S,S长度不超过50。
第二行包含一个整数N,表示询问的数目。(1 <= N <= 10)
以下N行每行包括一个S的子串s,s不为空串。
输出
对于每一个询问s,求出包含s的状态st,输出一行依次包含shortest(st)、longest(st)和endpos(st)。其中endpos(st)由小到大输出,之间用一个空格分割。
- 样例输入
-
aabbabd 5 b abbab aa aabbab bb
- 样例输出
-
b b 3 4 6 bab aabbab 6 aa aa 2 bab aabbab 6 bb aabb 4
SAM存个板子!hihocoder讲得真的很详细!通俗易懂!endpos集合从slink_tree的子节点递推出来,由于字符串长度很小,直接用long long存储该集合即可。
#include<cstdio>
#include<cstring>
using namespace std;
#define MAXL 50
#define MAXC 26
typedef long long ll;
int v[2*MAXL+10],__next[2*MAXL+10],first[2*MAXL+10],e;
void AddEdge(int U,int V){
v[++e]=V;
__next[e]=first[U];
first[U]=e;
}
char s[MAXL+10];//文本串
int len/*文本串长度*/;
struct SAM{
ll endposes[2*MAXL+10];
int endcnt[2*MAXL+10];
int n/*状态数0~n-1*/,maxlen[2*MAXL+10],minlen[2*MAXL+10],trans[2*MAXL+10][MAXC],slink[2*MAXL+10];
int new_state(int _maxlen,int _minlen,int _trans[],int _slink){
maxlen[n]=_maxlen;
minlen[n]=_minlen;
for(int i=0;i<MAXC;++i){
if(_trans==NULL){
trans[n][i]=-1;
}
else{
trans[n][i]=_trans[i];
}
}
slink[n]=_slink;
return n++;
}
int add_char(char ch,int u,int pos){
if(u==-1){
return new_state(0,0,NULL,-1);
}
int c=ch-'a';
int z=new_state(maxlen[u]+1,-1,NULL,-1);
endposes[z]=(1ll<<pos);
endcnt[z]=1;
int v=u;
while(v!=-1 && trans[v][c]==-1){
trans[v][c]=z;
v=slink[v];
}
if(v==-1){//最简单的情况,suffix-path(u->S)上都没有对应字符ch的转移
minlen[z]=1;
slink[z]=0;
return z;
}
int x=trans[v][c];
if(maxlen[v]+1==maxlen[x]){//较简单的情况,不用拆分x
minlen[z]=maxlen[x]+1;
slink[z]=x;
return z;
}
int y=new_state(maxlen[v]+1,-1,trans[x],slink[x]);//最复杂的情况,拆分x
slink[y]=slink[x];
minlen[x]=maxlen[y]+1;
slink[x]=y;
minlen[z]=maxlen[y]+1;
slink[z]=y;
int w=v;
while(w!=-1 && trans[w][c]==x){
trans[w][c]=y;
w=slink[w];
}
minlen[y]=maxlen[slink[y]]+1;
return z;
}
void dfs(int U){
for(int i=first[U];i;i=__next[i]){
dfs(v[i]);
endposes[U]|=endposes[v[i]];
endcnt[U]+=endcnt[v[i]];
}
}
void work_slink_tree(){
for(int i=1;i<n;++i){
AddEdge(slink[i],i);
}
dfs(0);
}
}sam;
int m;
int main(){
// freopen("hihocoder1441.in","r",stdin);
// freopen("hihocoder1441.out","w",stdout);
char T[MAXL+10];
scanf("%s",s);
len=strlen(s);
int U=sam.add_char(0,-1,0);
for(int i=0;i<len;++i){
U=sam.add_char(s[i],U,i);
}
sam.work_slink_tree();
scanf("%d",&m);
for(int i=1;i<=m;++i){
scanf("%s",T);
int lenT=strlen(T);
U=0;
for(int j=0;j<lenT;++j){
U=sam.trans[U][T[j]-'a'];
}
int k=0;
for(int j=0;j<len;++j){
if((sam.endposes[U]>>j)&1){
++k;
if(k==1){
for(int l=j-sam.minlen[U]+1;l<=j;++l){
putchar(s[l]);
}
putchar(' ');
for(int l=j-sam.maxlen[U]+1;l<=j;++l){
putchar(s[l]);
}
putchar(' ');
}
printf("%d%c",j+1,k==sam.endcnt[U] ? '
' : ' ');
}
}
}
return 0;
}