设每个点有x,y两个权值,求一棵生成树,使得sigma(x[i])*sigma(y[i])最小。
设每棵生成树为坐标系上的一个点,sigma(x[i])为横坐标,sigma(y[i])为纵坐标。则问题转化为求一个点,使得xy=k最小。即,使过这个点的反比例函数y=k/x最接近坐标轴。
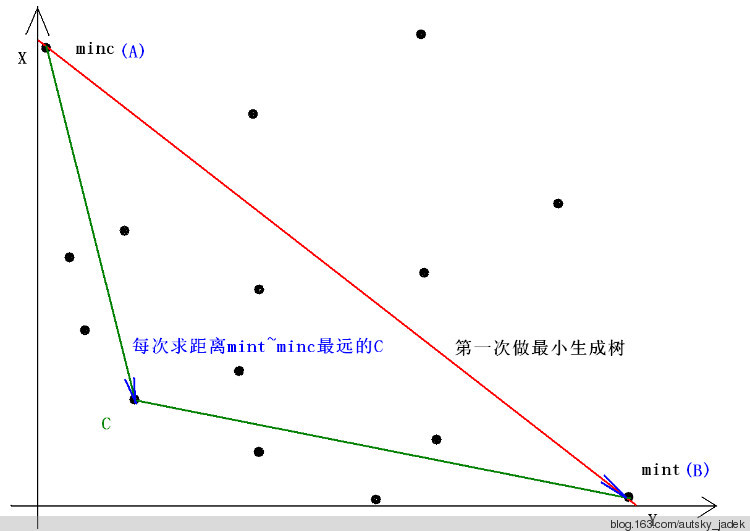
Step1:求得分别距x轴和y轴最近的生成树(点):A、B(分别按x权值和y权值做最小生成树即可)。
Step2:寻找一个在AB的靠近原点一侧的且离AB最远的生成树C,试图更新答案。
【怎么找????
——由于C离AB最远,所以S△ABC面积最大。
向量AB=(B.x - A.x , B.y - A.y)
向量AC= (C.x - A.x , C.y - A.y)
向量AB、AC的叉积(的二分之一)为S△ABC的面积(只不过叉积是有向的,是负的,所以最小化这个值,即为最大化面积)。
最小化:(B.x-A.x)*(C.y-A.y)-(B.y-A.y)*(C.x-A.x)
=(B.x-A.x)*C.y+(A.y-B.y)*C.x - A.y*(B.x-A.x)+A.x*(B.y-A.y)/*粗体为常数,不要管*/
所以将每个点的权值修改为 y[i]*(B.x-A.x)+(A.y-B.y)*x[i] 做最小生成树,找到的即是C。】
Step3:递归地分别往AC、BC靠近原点的一侧找。递归边界:该侧没有点了(即叉积大于等于零)。
BZOJ2395 裸题
Code:
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 using namespace std; 5 int res; 6 char c; 7 inline int Get() 8 { 9 res=0;c='*'; 10 while(c<'0'||c>'9')c=getchar(); 11 while(c>='0'&&c<='9'){res=res*10+(c-'0');c=getchar();} 12 return res; 13 } 14 struct Edge{int u,v,c,t,w;void read(){u=Get();v=Get();c=Get();t=Get();}}; 15 struct Point{int x,y;Point(const int &A,const int &B){x=A;y=B;}Point(){}}; 16 typedef Point Vector; 17 typedef long long LL; 18 Vector operator - (const Point &a,const Point &b){return Vector(a.x-b.x,a.y-b.y);} 19 int Cross(Vector A,Vector B){return A.x*B.y-A.y*B.x;} 20 bool operator < (const Edge &a,const Edge &b){return a.w<b.w;} 21 Edge edges[10001]; 22 int n,m,rank[201],fa[201]; 23 Point ans=Point(1000000000,1000000000),minc,mint; 24 inline void init() 25 { 26 memset(rank,0,sizeof(rank)); 27 for(int i=0;i<n;i++) 28 fa[i]=i; 29 } 30 int findroot(int x) 31 { 32 if(fa[x]==x) 33 return x; 34 int t=findroot(fa[x]); 35 fa[x]=t; 36 return t; 37 } 38 inline void Union(int U,int V) 39 { 40 if(rank[U]<rank[V]) 41 fa[U]=V; 42 else 43 { 44 fa[V]=U; 45 if(rank[U]==rank[V]) 46 rank[U]++; 47 } 48 } 49 inline Point Kruscal() 50 { 51 int tot=0; 52 Point now=Point(0,0); 53 init(); 54 for(int i=1;i<=m;i++) 55 { 56 int U=findroot(edges[i].u),V=findroot(edges[i].v); 57 if(U!=V) 58 { 59 Union(U,V); 60 tot++; 61 now.x+=edges[i].c; 62 now.y+=edges[i].t; 63 if(tot==n-1) 64 break; 65 } 66 } 67 LL Ans=(LL)ans.x*ans.y,Now=(LL)now.x*now.y; 68 if( Ans>Now || (Ans==Now&&now.x<ans.x) ) 69 ans=now; 70 return now; 71 } 72 void Work(Point A,Point B) 73 { 74 for(int i=1;i<=m;i++) 75 edges[i].w=edges[i].t*(B.x-A.x)+edges[i].c*(A.y-B.y); 76 sort(edges+1,edges+m+1); 77 Point C=Kruscal(); 78 if(Cross(B-A,C-A)>=0) 79 return; 80 Work(A,C); 81 Work(C,B); 82 } 83 int main() 84 { 85 scanf("%d%d",&n,&m); 86 for(int i=1;i<=m;i++) 87 edges[i].read(); 88 for(int i=1;i<=m;i++) 89 edges[i].w=edges[i].c; 90 sort(edges+1,edges+m+1); 91 minc=Kruscal(); 92 for(int i=1;i<=m;i++) 93 edges[i].w=edges[i].t; 94 sort(edges+1,edges+m+1); 95 mint=Kruscal(); 96 Work(minc,mint); 97 printf("%d %d ",ans.x,ans.y); 98 return 0; 99 }