方法一、简单递归
这个就不说了,小n怡情,大n伤身啊……当n=40的时候,就明显感觉到卡了,不是一般的慢。
1 //输出第n个 Fibonacci 数
2 #include <iostream>
3 using namespace std;
4
5 long long Fibonacci(int n)
6 {
7 if(n<=2) return 1;
8 else return Fibonacci(n-1) + Fibonacci(n-2);
9 }
10
11
12 int main()
13 {
14 int n;
15 while(cin>>n, n)
16 cout<<Fibonacci(n)<<endl;
17
18 return 0;
19 }
方案二、动态规划
1 //输出第n个 Fibonacci 数
2 #include <iostream>
3 #include <cstring>
4 #define MAXN 300
5 using namespace std;
6
7 long long F[MAXN];
8 int i;
9 long long Fibonacci(int n)
10 {
11 i++;
12 F[0]=1;
13 F[1]=1;
14 if(n<=2) return 1;
15 else
16 {
17 if(F[n]==0) // !!!!!!!!!!
18 F[n]=Fibonacci(n-1) + Fibonacci(n-2);
19 return F[n];
20 }
21 }
22
23
24 int main()
25 {
26 int n;
27 while(cin>>n, n)
28 {
29 i=0;
30 memset(F,0,sizeof(F));
31 cout<<Fibonacci(n)<<" ";
32 cout<<"调用"<<i<<"次"<<endl;
33
34 }
35 return 0;
36 }
【以上程序可以优化:既然只要求输出第n个斐波纳契数f(n),则只需用两个变量记录f(n-1)和f(n-2),不用开数组将整个1到n的斐波纳契数列都记录下来。】
最开始忘了 if(F[n]==0) 这个判断(17行),导致了很多次的重复计算——和递归算法一样多的次数。
以下是程序运行截图,上图为正确程序,下图为漏掉了 if(F[n]==0) 这个判断的错误程序。可以看出运行时间上的巨大差距:

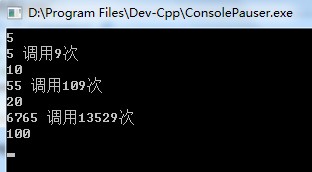
当输入n=100时,错误的程序很长很长一段时间内都还没计算出来。
方法三、for循环 + 数组
速度也非常快。
1 //输出第n个 Fibonacci 数
2 #include <iostream>
3 #include <cstring>
4 #define MAXN 300
5 using namespace std;
6
7 long long F[MAXN];
8 long long Fibonacci(int n)
9 {
10 F[0]=1;
11 F[1]=1;
12 if(n<=2) return 1;
13 else
14 {
15 for(int i=2; i<n; ++i)
16 F[i] = F[i-1] + F[i-2];
17 return F[n-1];
18 }
19 }
20
21
22 int main()
23 {
24 int n;
25 while(cin>>n, n)
26 {
27 memset(F,0,sizeof(F));
28 cout<<Fibonacci(n)<<endl;
29 }
30 return 0;
31 }