在讲解二叉查找树之前,先了解一下二分查找。
二分查找
我们使用有序数组存储键,经典的二分查找能够根据数组的索引大大减少每次查找所需的比较次数。
在查找时,我们先将被查找的键和子数组的中间键比较。如果被查找的键小于中间键,我们就在左子数组中继续查找,如果大于我们就在右子数组中继续查找,否则中间键就是我们要找的键。
一般情况下二分查找都比顺序查找快的多,它也是众多实际应用程序的最佳选择。对于一个静态表(不允许插入)来说,将其在初始化时就排序是值得的。
当然,二分查找也不适合很多应用。现代应用需要同时能够支持高效的查找和插入两种操作的符号表实现。也就是说,我们需要在构造庞大的符号表的同时能够任意插入(也许还有删除)键值对,同时也要能够完成查找操作。
要支持高效的插入操作,我们似乎需要一种链式结构。当单链接的链表是无法使用二分查找的,因为二分查找的高效来自于能够快速通过索引取得任何子数组的中间元素。为了将二分查找的效率和链表的灵活性结合起来,我们需要更加复杂的数据结构。
二叉查找树
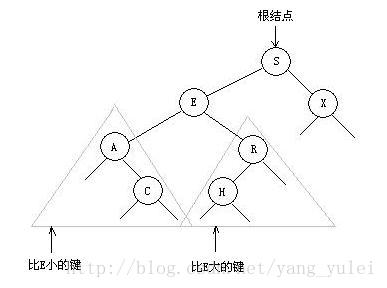
一颗二叉查找树(BST)是一颗二叉树,其中每个节点都含有一个可比较的键(以及相关联的值)且每个结点的键都大于其左子树中的任意结点的键而小于右子树的任意结点的键。
一颗二叉查找树代表了一组键(及其相应的值)的集合,而同一个集合可以用多颗不同的二叉查找树表示。
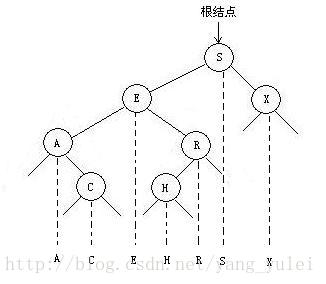
如果我们将一颗二叉查找树的所有键投影到一条直线上,保证一个结点的左子树中的键出现在它的右边,右子树中的键出现在它的右边,那么我们一定可以得到一条有序的键列。
查找
在二叉查找树中查找一个键的递归算法:
如果树是空的,则查找未命中。如果被查找的键和根结点的键相等,查找命中。否则我们就在适当的子树中继续查找。如果被查找的键较小就选择左子树,较大就选择右子树。
在二叉查找树中,随着我们不断向下查找,当前结点所表示的子树的大小也在减小(理想情况下是减半)
插入
查找代码几乎和二分查找的一样简单,这种简洁性是二叉查找树的重要特性之一。而二叉查找树的另一个更重要的特性就是插入的实现难度和查找差不多。
当查找一个不存在于树中的结点并结束于一条空链接时,我们需要做的就是将链接指向一个含有被查找的键的新结点。如果被查找的键小于根结点的键,我们会继续在左子树中插入该键,否则在右子树中插入该键。
分析
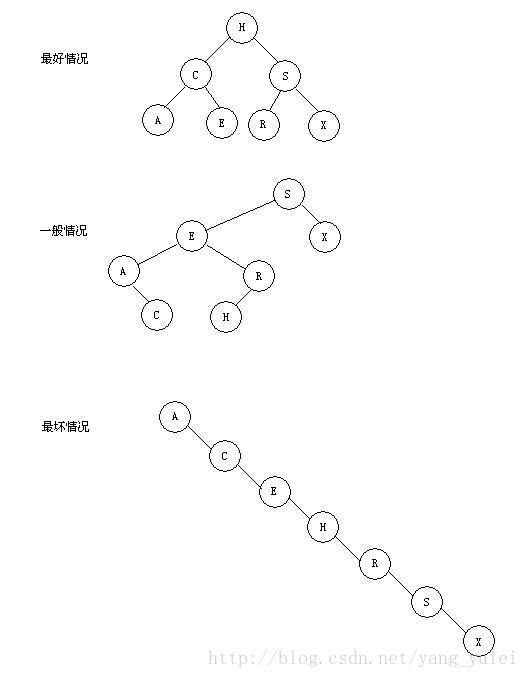
使用二叉查找树的算法的运行时间取决于树的形状,而树的形状又取决于键被插入的先后顺序。
在最好的情况下,一颗含有N个结点的树是完全平衡的,每条空链接和根结点的距离都为~lgN。在最坏的情况下,搜索路径上可能有N个结点。但在一般情况下树的形状和最好情况更接近。
我们假设键的插入顺序是随机的。对这个模型的分析而言,二叉查找树和快速排序几乎就是“双胞胎”。树的根结点就是快速排序中的第一个切分元素(左侧的键都比它小,右侧的键都比它大),而这对于所有的子树同样适用,这和快速排序中对于子数组的递归排序完全对应。
【在由N个随机键构造的二叉查找树中,查找命中平均所需的比较次数为~2lgN。 N越大这个公式越准确】
参考文章:https://blog.csdn.net/yang_yulei/article/details/26066409