[APIO2014]回文串

题目

只使用(sam)的做法真是太妙了

对于原串建立后缀自动机，之后将反串放上去匹配，发现我们会得到这样的情况

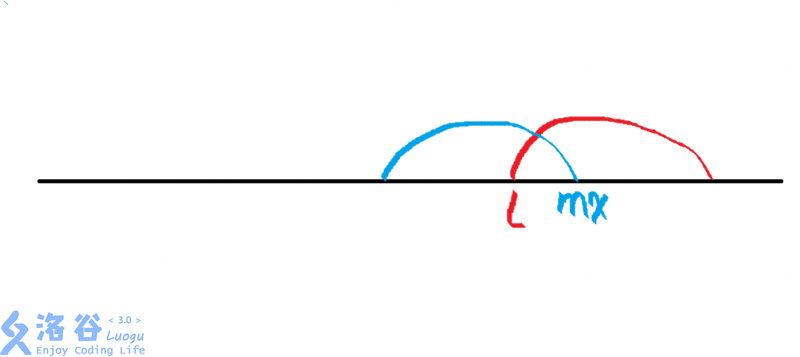
这里的(mx)是蓝色部分出现最靠后的位置

我们画的这是一个正串，我们的反串就是红色位置，和蓝色位置能产生匹配

于是我们把红色位置倒过来，就能和蓝色匹配

于是(S[l]=S[mx],S[l+1]=S[mx-1]...)

于是我们就可以断定([l,mx])这里是一个回文串

跳(link)会使得匹配长度减小，但是出现次数增加，所以我们还需要跳一波(link)

为什么是(maxpos)呢，这样是为了在其最后一次出现的时候统计所有本质不同的回文子串

如果前面有一段和红色部分相同的，那么就不会重复统计了

代码

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#define re register
#define LL long long
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
const int maxn=6e5+5;
inline int read() {
	char c=getchar();int x=0;while(c<'0'||c>'9') c=getchar();
	while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-48,c=getchar();return x;
}
int n,lst=1,cnt=1;
char S[maxn>>1];
int len[maxn],fa[maxn],son[maxn][26],pos[maxn],vis[maxn];
int A[maxn],tax[maxn>>1];LL sz[maxn];
LL ans;
inline void ins(int c,int o) {
	int p=++cnt,f=lst;lst=p;
	len[p]=len[f]+1,sz[p]=1;pos[p]=o;
	while(f&&!son[f][c]) son[f][c]=p,f=fa[f];
	if(!f) {fa[p]=1;return;}
	int x=son[f][c];
	if(len[f]+1==len[x]) {fa[p]=x;return;}
	int y=++cnt;
	len[y]=len[f]+1,fa[y]=fa[x],fa[x]=fa[p]=y;
	for(re int i=0;i<26;i++) son[y][i]=son[x][i];
	while(f&&son[f][c]==x) son[f][c]=y,f=fa[f];
}
int main() {
	scanf("%s",S+1);n=strlen(S+1);
	for(re int i=1;i<=n;i++) ins(S[i]-'a',i);
	for(re int i=1;i<=cnt;i++) tax[len[i]]++;
	for(re int i=1;i<=n;i++) tax[i]+=tax[i-1];
	for(re int i=cnt;i>=0;--i) A[tax[len[i]]--]=i;
	for(re int i=cnt;i>=0;--i) {
		int x=A[i];
		sz[fa[x]]+=sz[x];pos[fa[x]]=max(pos[x],pos[fa[x]]);
	}
	int now=1,l=0;
	for(re int i=n;i;--i) {
		while(now&&!son[now][S[i]-'a']) 
			now=fa[now],l=len[now];
		if(!now) {now=1;l=0;continue;}
		if(son[now][S[i]-'a']) 
			now=son[now][S[i]-'a'],l++;
		if(pos[now]<=i+l-1) {
			if(pos[now]>=i) ans=max(ans,(LL)(pos[now]-i+1)*sz[now]);
			for(re int k=fa[now];!vis[k]&&k;k=fa[k]) {
				if(pos[k]<=i+len[k]-1) 
					ans=max(ans,(LL)(pos[k]-i+1)*sz[k]);
				else break;
			}
		}
	}
	printf("%lld
",ans);
	return 0;
}