Problem description:
n枚硬币排成一个圈,A和B轮流从中取一枚或两枚硬币,不过取两枚时,所取的两枚硬币必须是连续的。硬币取走之后留下空位,相隔空位的硬币视为不连续的。A开始先取,取走最后一枚硬币的一方获胜。当双方都采取最优策略时,谁会获胜?
0<=n<=100000
Input
1
Output
A
n的数据过大时,状态过多,动态规划和搜索都会超时。
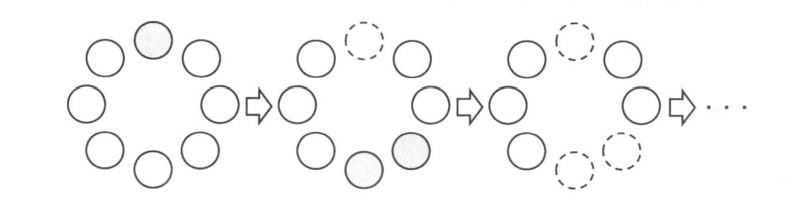
考虑将所有硬币分成两个完全相同对称的状态:

实际上我们发现这个时候是必败态,因为无论自己采取什么策略,对手只要在另一组采取相同的策略,就又回到了分成两个对称相同的状态。
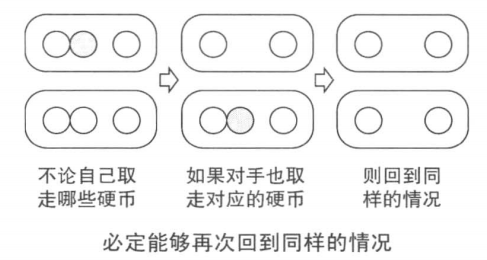
不断这样循环下去,总会轮到自己没有硬币,会因为对手取走了最后一枚硬币而败北。
A在第一步取走一个或两个硬币时,原本的圈就变成了n-1或n-2的链。这样只要B在链的中间根据链的奇偶,取走一个或两个硬币,就正好把硬币环分成了完全相同的两个部分。

这正如前面所说的,这是必败态。也就是说,当n<=2时,A必胜,当n>2时,A必败。
在这类游戏当中,作出对称的状态后再完全模仿对手的策略常常是非常有效的。