弹性碰撞

　　

　　

　　

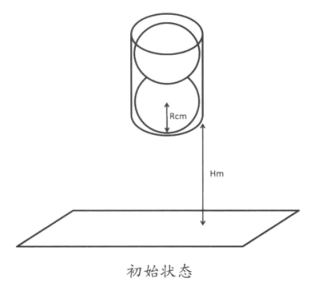
　　首先考虑一下只有一个球的情况。这时只是单纯的物理问题。从高为 H 的位置下落的话需要花费的时间是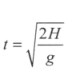，这样的话，在 T 时刻，令 k 为满足 kt ≤ T 的最大整数，那么

　　

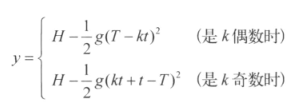
　　接下来考虑多个球的情况。乍一看，因为多个球之间会有碰撞，必须对物理运动进行模拟，事实上没有这个必要。回忆一下一个题目 “ Ants ”。在那道题目中两只蚂蚁相遇后并不是各自折返，而是当做擦身而过继续走下去，于是问题就简化了。

　　这里的问题可以用同样的方法思考。首先来考虑一下 R = 0 的情况。如果认为所有的球都是一样的，就可以无视它们的碰撞，视为直接互相穿过继续运动。由于在有碰撞时球的顺序不会发生改变，所有忽略碰撞，将计算得到的坐标进行排序后，就能知道每个球的最终位置。那么， R > 0 时要怎么考虑？这种情况下的处理方式基本相同，对应从下方开始的第 i 个球，在按照 R = 0 计算的结果上加上 2Ri 就好了。

const double g = 10.0;

int N, H, R, T;
double y[MAX_N];    // 球的最终位置

// 求出 T 时刻球的位置
double calc(int T) {
    if (T < 0) return  H;
    double t = sqrt(2 * H / g);
    int k = (int) (T / t);
    if (k % 2 == 0) {
        double d = T - k * t;
        return H - g * d * d / 2; 
    }
    else {
        double d = k * t + t - T;
        return H - g * d * d / 2;
    }
} 

void solve() {
    for (int i = 0; i < N; i++)
        y[i] = calc(T - i);
    sort(y, y + N);
    for (int i = 0; i < N; i++)
        printf("%.2f%c", y[i] + 2 * R * i / 100.0, i + 1 == N ? '
' : ' ');    
}