在反转那篇文章中,为了尝试第一行的所有可能性,使用了集合的整数表现。在程序中表示集合的方法有很多种,当元素数比较少时,像这样用二进制码表示比较方便。集合{0, 1, ..., n-1} 的子集 S 可以用如下的方式编码成整数。
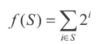
像这样表示之后,一些集合运算可以对应地写成如下方式。
(1) 空集Ø ------------------------------------------------------------> 0
(2)只含有第 i 个元素的集合{ i } ----------------------------------> 1 << i
(3)含有全部 n 个元素的集合{0, 1, ..., n-1} --------------> (1 << n) - 1
(4)判断第 i 个元素是否属于集合 S ------------------------------> if (S >> i & 1)
(5)向集合中加入第 i 个元素 S υ { i } ----------------------------> S | 1 << i
(6)从集合中删去第 i 个元素 S { i } -----------------------------> S & ~ (1 << i)
(7)集合 S 和 T 的并集 S υ T -------------------------------------> S | T
(8)集合 S 和 T的交集 S ∩ T --------------------------------------> S & T
此外,想要将集合{ 0, 1, ..., n-1} 的所有子集枚举出来的话,可以像下面这样书写
for ( int S = 0; S < 1 << n; S++) { //对子集的操作 }
按照这个顺序循环的话, S 便会从空集开始,然后按照 {0} 、{1}、{0,1}、....、{0, 1, ...,n-1} 的升序顺序枚举出来。
接下来介绍一下如何枚举某个集合 sup 的子集。这里 sup 是一个二进制码,其本身也是某个集合的子集。例如给定 01101101 这样的集合,要将 01100000 或者 00101101 等子集枚举出来。前面是从 0 开始不断加 1 来枚举出来全部的子集。此时, sub + 1 并不一定是 sup 的子集。而 (sub + 1) & sup 虽然是 sup 的子集,可是很有可能依旧是 sub,没有任何改变。
所以我们要反过来, 从 sup 开始每次减 1 直到 0 为止。由于 sub - 1 并不一定是 sup 的子集,所以我们把它与 sup 进行按位与 &。这样的话就可以将 sup 所有的子集按照降序序列枚举出来。 (sub - 1)& sup 会忽略 sup 中的 0 而从 sub 中减去 1。
int sub = sup; do{ //对子集的处理 sub = (sub - 1) & sup; } while(sub != sup); // 处理完 0 之后,会有 -1 & sup = sup
最后介绍下枚举 {0,1,...,n-1} 所包含的所有大小为 k 的子集的方法。通过使用位运算,我们可以像如下代码所示简单地按照字典序升序地枚举出所有满足条件的二进制代码。
int comb = (1 << k - 1); while (comb < 1 << n) { //这里进行针对组合的处理 int x = comb & -comb, y = comb + x; comb = ((comb & ~y) / x >> 1) | y; }
下面的我还没看.....

