尺取法通常是指对数组保存一对下标(起点,终点),然后根据实际情况交替推进两个端点直到得出答案的方法。
1.


由于所有的元素都大于零,如果子序列 [s, t] 满足 as + .... at ≥ S,那么对于任何的 t < t' 一定有 as + .... at‘-1 ≥ S。
此外对于区间[ s, t]上的总和来说,如果令 sum(i)= a0 + .... + ai - 1,那么 as + .... at - 1 = sum(t)- sum(s)。
因此预先以O(n)的时间计算好 sum 的话,就可以以O(1)的时间计算区间上的总和。这样的haul,子序列的起点 s 确定以后,便可以用二分搜索快速地确定使序列和不小于 S 的结尾的最小值。
int n, S; int a[MAX_N]; int sum[MAX_N + 1]; void solve() { for (int i = 0; i < n; i++) sum[i + 1] = sum[i] + a[i]; if (sum[n] < S) { printf("0 "); return; } int res = n; for (int s = 0, sum[s] + S <= sum[n]; s++) { int t = lower_bound(sum + s, sum + n, sum[s] + S) - sum; res = min(res, t - s); } printf("%d ", res); }
复杂度为O(n log n)。但我们还可以更加高效地来求解。
设以 ai 开始总和最初大于 S 时的连续子序列为 as + .. +at ,这时 as+1 + ... + at - 2 < as +...+ at-2 < S
所以从 as+1 开始总和最初超过 S 的连续子序列如果是 as + .. +at‘ +1 的话,则必然有 t ≤ t'。利用这一特性便可以设计出如下算法:
(1)以 s = t = sum = 0 初始化;
(2)只要依然有 sum < S,就不断将 sum 增加 at ,并将 t 增加 1;
(3)如果(2)中无法满足 sum ≥ S 则终止。否则的话,更新 res = min(res, t - s);
(4)将 sum 减去 as,s 增加 1 然后回到(2)。
对于这个算法,因为 t 最多变化 n 次,因此只需O(n)的复杂度就可以求解这个问题。
void solve() { int res = n + 1; int s = 0, t = 0, sum = 0; for (;;) { while (t < n && sum < S) sum += a[t++]; if (sum < S) break; res = min(res, t - s); sum -= a[s++]; } if (res > n) res = 0; //解不存在 printf("%d ", res); }
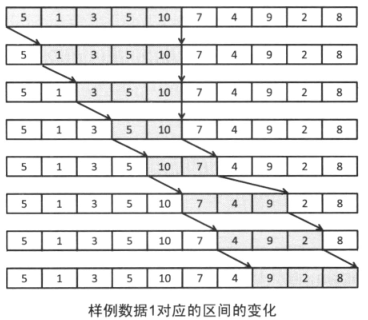
像这样反复地推进区间的开头和末尾,来求取满足条件的最小区间的方法称为尺取法。
2.


我们假设从某一页 s 开始阅读,为了覆盖所有的知识点需要阅读到 t。这样的话可以知道如果从 s + 1 开始阅读的话,那么必须阅读到 t' ≥ t 页为止。由此这题也可以使用尺取法。
在某个区间[ s, t ] 已经覆盖了所有的知识点的情况下,下一个区间 [ s + 1, t' ] (t' ≥ t)要如何求出呢?
所有的知识点都被覆盖 等价于 每个知识点出现的次数都不小于 1
由以上的等价关系,我们可以用二叉树等数据结构来存储 [ s, t ]区间上每个知识点的出现次数,这样把最开头的页 s 去除后便可以判断 [ s + 1, t ] 是否满足条件。
从区间的最开头把 s 取出之后,页 s 上书写的知识点的出现次数就要减一,如果此时这个知识点的出现次数为 0 了,在同一个知识点再次出现前,不停将区间末尾向后推进即可。每次在区间末尾追加页 t 上的知识点的出现次数加 1,这样就完成了下一个区间上各个知识点出现次数的更新,通过重复这一操作可以以O(P log P)的复杂度求出最小的区间。
int p; int a[MAX_P]; void solve() { // 计算全部知识点的总数 set<int> all; for (int i = 0; i < P; i++) all.insert(a[i]); int n = all.size(); int s = 0, t = 0, num = 0; map<int, int> count; int res = P; for(;;) { while (t < P && num < n) if (count[a[t++]]++ == 0) // 出现新的知识点 num++; if (num < n) break; res = min(res, t - s); if (--count[a[s++]] == 0) //某个知识点的出现次数为 0 了 num--; } printf("%d ", res); }