二分搜索法是通过不断缩小可能存在的范围,从而求得问题最优解的方法。
1. 从有序数组中查找某个值
给定长度为 n 的单调非递减数列 a0......an,和一个数 k,求满足 ai ≥ k 条件的最小的 i,不存在的情况下输出n。
int n, k; int a[MAX_N]; // STL void solve() { int ans = *lower_bound(a, a + n, k); printf("%d ", ub); } // void solve() { //初始化解的范围 int lb = -1, ub = n; //重复循环,直到解的范围不大于一 while (ub - lb > 1) { int mid = (lb + ub) / 2; // 如果mid满足条件,则解的存在范围变为(lb, mid] if (a[mid] >= k) ub = mid; // 如果不满足,则解的范围变为(mid, ub] else lb = mid; } printf("%d ", ub); }
求满足某个条件C(x)的最小的 x 这一问题。对于任意满足C(x) 的 x, 如果所有的 x' ≥ x 也满足C(x')的话,我们就可以用二分搜索来求得最小的 x。首先将区间的左端点初始化为不满足C(x)的值,右端点初始化为满足C(x) 的值,然后每次取中点 mid = (lb + ub)/ 2,判断 C(mid)是否满足并缩小范围,直到 ( lb, ub ] 足够小为止。最后 ub 就是需要求的最小值。
最大化的问题也可以用同样的方法求解。
2. 假定一个解并判断是否可行


这个问题用二分搜索可以非常容易地求得答案。让我们套用二分搜索的模型来解决这个问题。
令: 条件 C(x) := 可以得到 K 条长度为 x 的绳子
则问题就变成了求满足 C(x)条件的最大的 x。在区间初始化时,只需要用充分大的数 INF 作为上界即可: lb = 0, ub = INF.
现在的问题是是否可以高效地判断 C(x)。由于长度为 Li的绳子最多可切出 floor(Li / x) 段长度为 x 的绳子,因此:
C(x) = (floor(Li / x)的总和是否 ≥ K)
复杂度为 O(N)
int N, K; double L[MAX_N]; //判断是否满足条件 bool C(double x) { int num = 0; for (int i = 0; i < N; i++) num += (int) (L[i] / x); return num >= K; } void solve() { //初始化解的范围 double lb = 0, ub = INF; for (int i = 0; i < 100; i++) { double mid = (lb + ub) / 2; if (C(mid)) lb = mid; else ub = mid; } printf("%.2f ", floor(ub * 100) / 100); }
像这样,如果在求解最大化或最小化问题中,能够比较简单地判断条件是否满足,那么使用二分搜索法就可以很好地解决问题。
二分搜索法的结束判定
在输出小数的问题中,一般都会指定允许的误差范围或者是指定输出中小数点后面的位数。因此在使用二分搜索法时,有必要设置合理的结束条件来满足精度要求。在上面的程序中,我们指定了循环次数作为终止条件。一次循环可以把区间范围缩小一半,也可以把终止条件设为像 (ub - lb ) > EPS 这样,指定一个区间大小。在这种情况下,如果 EPS 取值太小,就可能会因为浮点数精度的原因导致陷入死循环,要小心。
3. 最大化最小值


类似的最大化最小值或者最小化最大值的问题,通常用二分搜索就可以很好地解决。
定义: C(d) := 可以安排牛的位置使得最近的两头牛的距离不小于 d
那么问题就变成了求满足 C(d)的最大的 d。另外,最近的间距不小于 d 也可以说成是所有牛的间距都不小于 d,因此就有
C(d)= 可以安排牛的位置使得任意的牛的间距都不小于 d
这个问题的判断可以使用贪心法就可以非常任意地求解:
对牛舍的位置 x 进行排序;
把第一头牛放进 x0 的牛舍;
如果第 i 头牛放入了 xj 的话,第 i + 1 头牛就要放入满足 xj + d ≤ xk 的最小的 xk 中;
每一次判断对每头牛最多进行一次处理,因此复杂度为 O(N)。
int N, M; int x[MAX_N]; bool C(int d) { int last = 0; for (int i = 1; i < M; i++) { int crt = last + 1; while(crt < N && x[crt] - x[last] < d) crt++; if (crt == N) return false; last = crt; } return true; } void solve() { sort(x, x + N); int lb = 0, ub = INF; while (ub - lb > 1) { int mid = (lb + ub) / 2; if (C(mid)) lb = mid; else ub = mid; } printf("%d ", lb); }
4. 最大化平均值



一般最先想到的方法是把物品按照单位价值排序,从小到大贪心地进行选取。但是这个方法是不可行的。实际上用二分搜索可以很好地解决。
定义: 条件 C(x) := 可以选择使得单位重量的价值不小于 x
因此原问题就变成求满足 C(x)的最大的 x。那么该如何判断 C(x)是否可行?假设我们选了某个物品的集合 S,那么它们的单位重量的价值是

因此就变成了判断是否存在 S 满足下面条件
 变形得
变形得 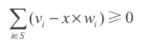
因此,可以对(vi - x * wi)的值进行排序贪心地进行选取。因此就变成了
C(x)= ((vi - x * wi)从大到小排列中的前 k 个和不小于 0)
每次判断的复杂度是O(n log n)。
int n, k; int w[MAX_N], v[MAX_N]; double y[MAX_N]; // v - x * w bool C(double x) { for (int i = 0; i < n; i++) y[i] = v[i] - x * w[i]; sort(y, y + n); double sum = 0; for (int i = 0; i < k; i++) sum += y[n - i - 1]; return sum >= 0; } void solve() { double lb = 0, ub = INF; for (int i = 0; i < 100; i++) { double mid = (lb + ub) / 2; if (C(mid)) lb = mid; else ub = mid; } printf("%.2f ", ub); }