leetcode62

使用排列组合计算公式来计算，注意使用long long型数据保证计算不会溢出。

class Solution {
public:
    long long FA(long long a) //定义阶乘函数FA
    {
        long long x = 1;//定义变量b
        for (int i = 1; i <= a; i++)//计算阶乘 
            x *= i;
        return x;//返回值得到b=a！ 
    }

    long long FA(long long a, long long b) //定义阶乘函数FA
    {
        //long long b = 1;//定义变量b    
        long long x = 1;
        for (int i = b; i <= a; i++)//计算阶乘 
            x *= i;
        return x;//返回值得到b=a！ 
    }

    int uniquePaths(int m, int n) {
        long long a = FA(m - 1 + n - 1, max(m, n));
        long long b = FA(min(m, n) - 1);
        return (int)(a / b);
    }
};

补充一个使用dp的方案，python 实现：

class Solution:
    def uniquePaths(self, m: 'int', n: 'int') -> 'int':
        dp =[[0 for col in range(n)] for row in range(m)]        
        for i in range(m):
            dp[i][0] =  1

        for j in range(n):
            dp[0][j] = 1
        print(dp)
        for i in range(1,m):
            for j in range(1,n):
                dp[i][j] = dp[i-1][j] + dp[i][j-1]
        return dp[m-1][n-1]

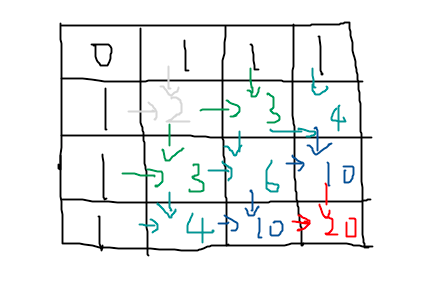
初始化index==0的行和index==0的列，起点为0，其他都是1（黑色）。

然后从(1,1)开始计算，可以一行一行的计算，也可以一列一列的计算，也可以按对角线计算，总之一步一步的推进，一直计算到(i,j)元素（红色），即为所求。

注意，dp[i][j]==dp[m-1][n-1]。