一,
这是最常见的二分查找法了。就是在一次次的排除中,让头和尾相遇。若头反超了尾,还没有找到,那就是没有了,否则位于头尾之间的中一定可以取到想要的数据
//并不是一定要中间值,只是中间值比较快,差个1也可以 #define MAX 100000 int a[MAX] = { 0 }; void FindNum(int data) { int tou = 0, wei = MAX - 1; int flag = -2; //标记有没有找到 data int count = 0; //记录是第几次查找 while (tou <= wei) { int zhong = (tou + wei) / 2; printf("tou=%d,wei=%d,zhong=%d,count=%d ", tou, wei, zhong, ++count); if (data == a[zhong]) { printf("看zhong,找到了%d ",a[zhong]); flag = 1; break; } else if (data > a[zhong]) { tou = zhong + 1; } else wei = zhong - 1; } if (flag == -2) printf("找不到 "); } int main(void) { for (int i = 0; i < MAX ; i++) //要查找的数组,1~MAX { a[i] = i; } int data; while (scanf("%d", &data) != EOF) { FindNum(data); }return 0; }
二,
先概述一下下面这个二分法吧。
1,此法判断不了有没有找到数据,最后判断还是要因题而异,自己判断。
2,if 执行的那条语句 就是最后找到的data。
#define MAX 100000 int a[MAX] = { 0 }; void FindNum(int data) { int tou = 0, wei = MAX - 1; int flag = -2; //标记有没有找到 data int count = 0; //记录是第几次查找 while (tou <= wei) { int zhong = tou + (wei - tou) / 2; printf("tou=%d,wei=%d,zhong=%d,count=%d ", tou, wei, zhong, ++count); if (a[zhong]< data) // 也可以换成 >,只是后面的都要换 tou = zhong + 1; else wei = zhong - 1; } printf("看tou,找到%d了 ", tou); } int main(void) { for (int i = 0; i < MAX; i++) { a[i] = i; } int data; while (scanf("%d", &data) != EOF) { FindNum(data); }return 0; }
之前一直无法理解为什么这样子也可以用二分法,不过我最后一次次尝试,终于想到一个不追究过程,就可以看出循环后 tou和wei在哪里的方法。
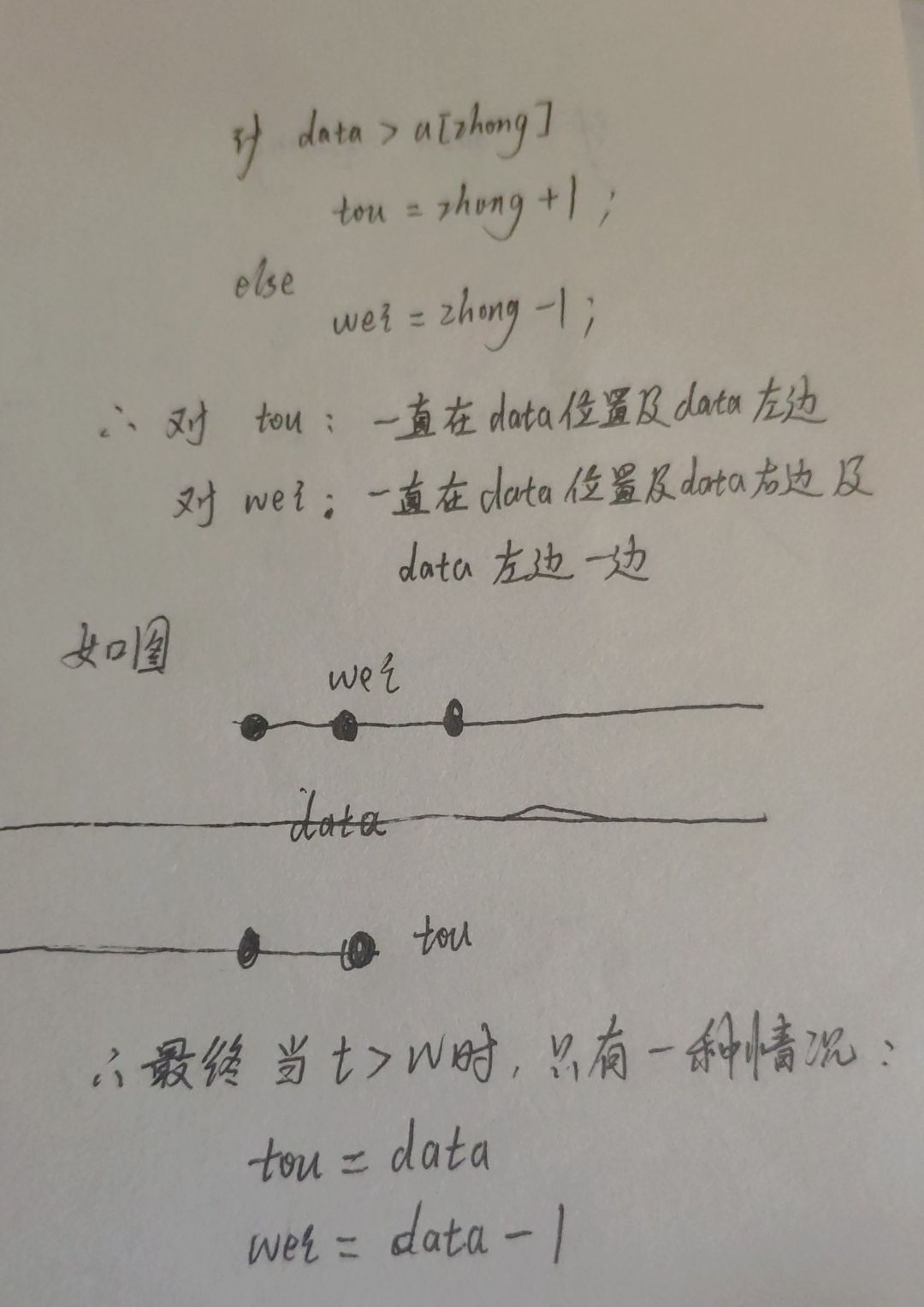
三,
下面这个可以说是二的应用了:查询小于等于x且下标最大的数字的下标
这个也可以用上面方法画出结果来。
#define N (int)1e5+5 int a[N], n; int findU(int data) { int L = -1, R = n; while (L + 1 < R) { int mid = L + (R - L) / 2; if (a[mid] <= data) //这个也可换成 >,L与R 换一下,还是 return L,效果不变 L = mid; else R = mid; } return L; } int main(void) { scanf("%d", &n); for (int i = 0; i < n; i++) { scanf("%d", &a[i]); } int x; while (scanf("%d", &x) != EOF) { printf("下标为%d ", findU(x)); } system("pause"); return 0; }
最终有几种情况 (因为已经说了判断不出来是否找不找的到)

当然这个换一下也可以找大于等于x且下标最小的数字的下标,具体的还是不去多讲,给大家留下思考的空间。
综上就是现在的我对二分法的理解了。共勉之!
========== ========== ======== ======= ====== ====== ==== === == =
问刘十九 白居易 唐
绿蚁新醅酒,红泥小火炉。
晚来天欲雪,能饮一杯无?