前言:这只是我的一个学习笔记,里边肯定有不少错误,还希望有大神能帮帮找找,由于是从小白的视角来看问题的,所以对于初学者或多或少会有点帮助吧。
1:人工全连接神经网络和BP算法
<1>:人工神经网络结构与人工神经网络可以完美分割任意数据的原理:
本节图片来源于斯坦福Andrew Ng老师coursea课件(此大神不多介绍,大家都懂)
在说明神经网络之前,先介绍一下神经网络的基础计算单元,感知器。
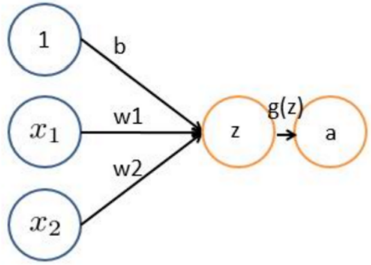
上图就是一个简单的感知器,蓝色是输入的样本,g(z)是激活函数,z=x1*w1+…,a=g(z)
这个东西可以用来干什么呢?我们可以令b=-30,w1=20,w2=20,此时限制输入的x1和x2为0或者1,激活函数为sigmoid函数:
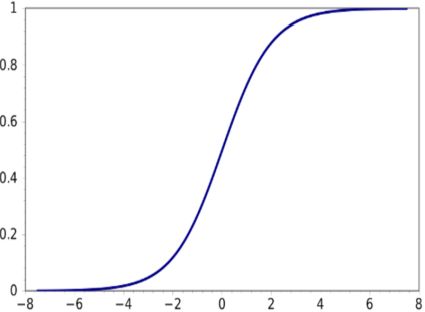
上图为sigmoid函数图像,可以看出当x很大时,此函数趋于1,当x很小时,此函数趋于0,写出真值表,可以发现这个感知器完成了一个逻辑与的操作。
| X1 | X2 | z | A |
| 0 | 0 | -30 | 0 |
| 0 | 1 | -10 | 0 |
| 1 | 0 | -10 | 0 |
| 1 | 1 | 10 | 1 |
将参数修改为b=-10,w1=20,w2=20,此时感知器又完成了一个逻辑或的操作,真值表就不写了,也就是说改变这些圆圈圈之间的传递参数,可以使这个感知器完成逻辑或和逻辑与的操作。当然对一个输入取非也不会有问题(b=10,w1=-20)。
因此,我们可以改变连接参数,从而使感知器完成与、或、非的操作。而将两层感知器连接起来,不就可以完成或非、与非、异或等操作了呗。
举一个例子,比如让一个神经网络分割下图圆圈和×:

这里重新将逻辑或和逻辑与画成类似上图的格式:


而我们要达到的目标则为:
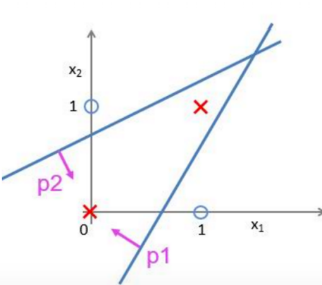
所以想要分割这两组点,第一层求一次或得到一个神经元,再求一个与得到另一个神经元,第二层求与就能得到上图结果了:
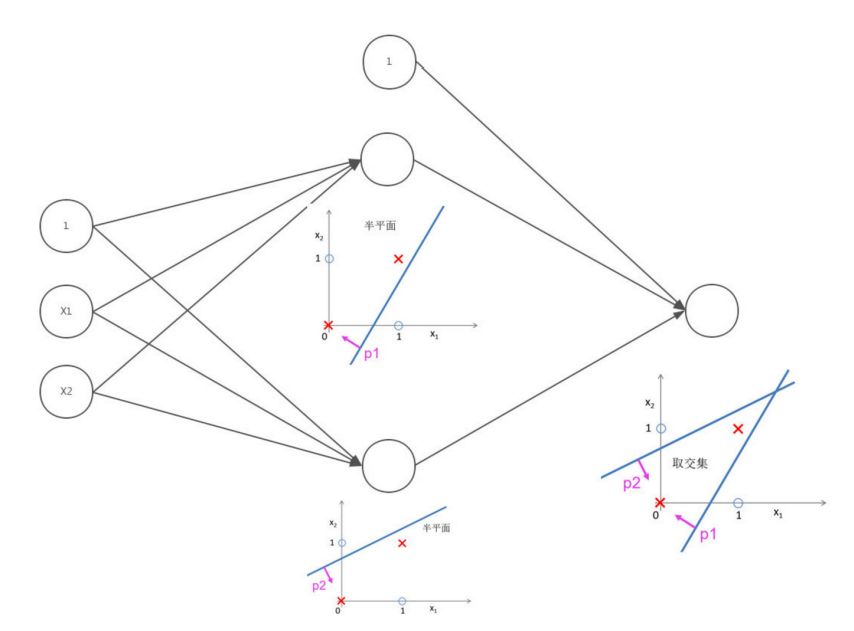
神经网络就是这样分割一个普通线性分类器很难分割的区域的
当神经元和神经网络的层数更高的时候,区分下面的数据也就不是什么问题了:

<2>:神经网络的结构和前向运算:
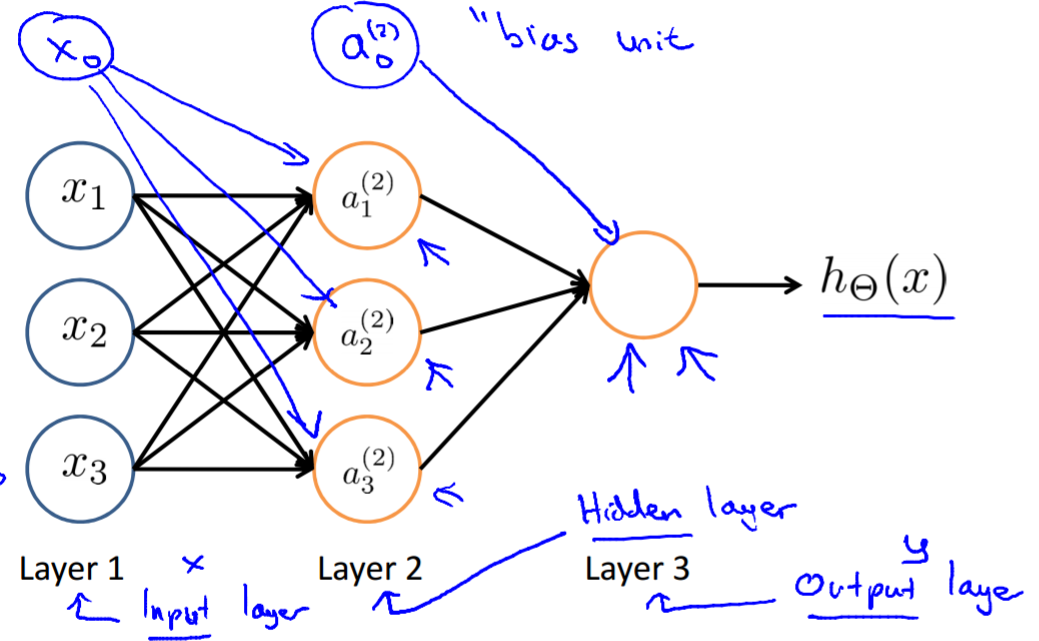
上图是Andrew Ng老师课程中的截图,这就是一个典型的神经网络,我们设( heta ^{(j)} )为j层到j+1层的传递矩阵,从输入层(蓝色)到中间的第二层,就有:
( a_{1}^{(2)} = g( heta_{10}^{(1)}x_{0}+ heta_{11}^{(1)}x_{1}+ heta_{12}^{(1)}x_{2}+ heta_{13}^{(1)}x_{3}) )
( a_{2}^{(2)} = g( heta_{20}^{(1)}x_{0}+ heta_{21}^{(1)}x_{1}+ heta_{22}^{(1)}x_{2}+ heta_{23}^{(1)}x_{3}) )
( a_{3}^{(2)} = g( heta_{30}^{(1)}x_{0}+ heta_{31}^{(1)}x_{1}+ heta_{32}^{(1)}x_{2}+ heta_{33}^{(1)}x_{3}) )
同理,第二层到输出层:
( h_{ heta}(x)=a_{1}^{(3)}=g( heta_{10}^{(2)}x_{0}+ heta_{11}^{(2)}x_{1}+ heta_{12}^{(2)}x_{2}+ heta_{13}^{(2)}x_{3}) )
注意这个神经网络的输出只有一个值而神经网络的输出可以有任意个,这里仅以此为例不再展开写,上边就是当已知每一层之间的系数矩阵时,神经网络求解的过程。
只要我们可以通过某种训练手段的得到神经网络各层之间的系数矩阵,那么神经网络就可以用来完成机器学习任务了。
从这里开始,将通过一个例子来说明,感觉这样子可以描述的更清楚些吧。可能也是应为我比较笨。。。
我们假设有m=500张样本图片,每个图片的分辨率是3*3而且都是黑白的,图片的label(标签)有3类,分别是烤鸡、烤鸭和烤全羊。我们构建一个双隐层的神经网络来判断任意一个输入的3*3图片是什么东西。这个神经网络只用来举例,一个9像素的图片当然什么实际的意义了。。。
这个神经网络的结构就是下边这个样子了:
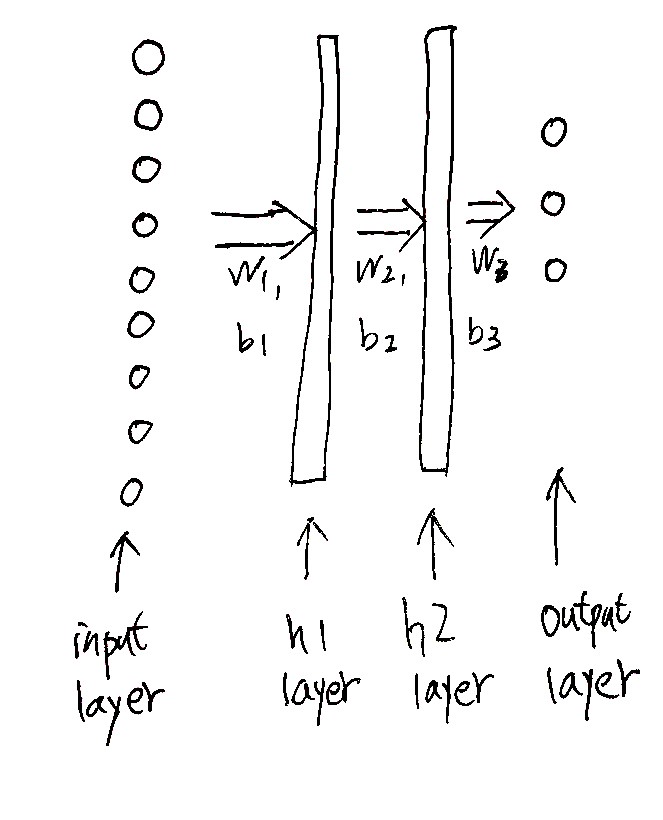
输入层是9个像素点的灰度值组成的向量X,有m=500个样本,所以dim(X)=500*9,中间两个隐层我们假设它们各有14个节点, (h_1)一个隐层(hidden layer),(dim(h_1))=500*14,(h_2)层是第二个隐层,(dim(h_2))=500*14,output就是输出层,有3个类别分别表示鸡,鸭,羊。维度当然是500*3了,参数W的维度分别是9*14,9*14,b则是一个500*14,500*14的矩阵,但b的每一行都是一样的,=>符号表示全连接,如果彻底画出来是这个样子的(懒得用visio画了,没啥意义)

对于bias项b,还可以这样理解:在每一层中加一个节点,这个节点固定值为1,从这个节点映射到下一层的每一个节点的参数组成的向量就是参数b,对于500个样本,就是每一个样本行都加上这个bias项了。
在numpy中,这么操作:
z1 = X.dot(W1) + b1 #这里b1是1*14的 a1 = np.tanh(z1) #激活函数还有tanh、ReLU等等 z2 = a1.dot(W2) + b2 …
X*W1出来是500*14,在numpy中加b1(1*14)就是在X*W1的每一行都加b1,同理,如果加某个500*1的向量,是每一列都加这个向量。这么设计有点困惑呢。。。数学老师说矩阵加法维度不一致不让加的。
计算假设函数的公式就是下边这样:
( h_1=g(x*W_1+b_1) )
( h_2=g(h_1*W_2+b_2) )
( output=h_3=g(h_2*W_3+b_3) )
这样,对于这500个样本,每个样本的每一类的得分就都计算出来了。当然由于参数组是随机搞到的,得分不一定合理,比如一个标签是烤鸭的样本,烤鸭的得分反而是最低的,这都有可能,想要定性的衡量这套参数的靠谱程度,从而优化这套参数,就要介绍下一个工具,损失函数了。
<3>:损失函数(cost function),判断当前这套参数的性能:
损失函数是干啥的呢,在这个例子中我们有m个样本,然后我们随便搞一套参数组合,把这m个样本分别扔到神经网络中去运算出输出,由于我们知道这些样本的标签,所以就可以判断我们之前随便搞的这套参数组合能不能用来求解未知的数据,比如有一枚数据的标签是烤鸭,将这个数据扔到神经网络里,算出来的得分是:
烤鸭:2分,烧鸡:12分,烤全羊:-78分
很明显嘛,这套参数得到的值不对,按照神经网络的值不就把鸭子认成鸡了嘛。损失函数就是衡量这个不对的程度的函数,顾名思义嘛,损失函数的值越小,说明你这套参数就越靠谱,越能表达样本总体的特征。
在Andrew Ng课程中,老师直接给出了损失函数:
( j( heta)=-frac{1}{m}[sumlimits_{i=1}^msumlimits_{k=1}^Ky_k^{(i)}logh_{ heta}(x^{(i)})_{k}+(1-y_k^{(i)})log(1-h_{ heta}(x^{(i)})_{k})]+frac{lambda}{2m}sumlimits_{l=1}^{L-1}sumlimits_{i=1}^{S_l}sumlimits_{j=1}^{S_{l+1}}( heta_j^{(l)})^2 )
K means the number of output units.
L means total number of layers in the network.
(S_l)means number of units in layer l(not counting bias unit).
m是样本数量.
这个损失函数其实是一个logistic regression问题的交叉熵损失(cross entropy loss),一步一步来看这个损失是怎么来的哈,比较复杂。我举的这个栗子是softmax回归问题,就是多分类问题。
第一步是对输出进行归一化处理(normalize),我们可以将得分转换成概率形式,假设某个标签为烤鸭的样本得分是:
烤鸭:2分,烧鸡:12分,烤全羊:-78分
归一化为:
烤鸭:(frac{e^2}{e^2+e^{128}+e^{-78}})
烧鸡:(frac{e^{12}}{e^2+e^{128}+e^{-78}})
烤全羊:(frac{e^{-78}}{e^2+e^{128}+e^{-78}})
这样,输出的样本得分就变成了:
烤鸭:4.5*10^-5,烧鸡:几乎是1,烤全羊:8.2*10-40
这样子就可以很方便的和样本标签做比较了,比如这个样本的标签是烤鸭,标签向量y就是[1,0,0]了。不是的话需要转换成这种形式。
交叉熵损失,就是将这些概率和标签中正确的概率向量的差加起来再求一个负对数,刚刚的数据比较庞大,我们假设计算得到的输出概率向量为[0.1,0.5,0.4],这个意思就是神经网络认为你输入的这张图片有0.1的概率是烤鸭,0.5的概率是烧鸡…,但实际输入的样本图片的标签是烤鸭,也就是[1,0,0]。那么他在每一个类别上的损失就是[1-0.1,0.5-0,0.4-0]
而cross entropy loss就等于
(-frac{1}{m}[log(1-0.1)+log0.5+log0.4])
现在再感受一下这个式子。恍然大悟吧。如果这个类别标签是0,说明你输出的softmax概率全部是损失,如果这个类标签是1,你输出的概率本该是1,但差了1-p那么多,所以损失就是1-p。
( j( heta)=-frac{1}{m}[sumlimits_{i=1}^msumlimits_{k=1}^Ky_k^{(i)}logh_{ heta}(x^{(i)})_{k}+(1-y_k^{(i)})log(1-h_{ heta}(x^{(i)})_{k})] )
K means the number of output units.
L means total number of layers in the network.
(S_l)means number of units in layer l(not counting bias unit).
恩我是应为笨才说的这么清楚的。。。
至于为毛叫交叉熵损失。。等我学完信息论再回答吧,留个坑。
有了损失函数的定义后,我们可以随机初始化一组系数矩阵,然后使用梯度下降的方法找到一组(使用大量的样本)令损失函数最小的系数矩阵,这就是SGD(随机梯度下降)
<4>:BP与SGD:
在介绍SGD算法之前,先简单说一下什么是梯度下降(gradient descent)。我们假设有一个凸函数如图所示,如何从随机的一点逐渐收敛到这个函数的最小值呢?

下边的伪代码就是梯度下降。当循环次数达到一定数量时,此时的x就非常接近f(x)的最小值了。
Repeat until convergence{
(delta=alphafrac{d}{dx}f(x))
x=x-(delta)
}
a是一个更新率,当a很小时梯度收敛的很慢,当a较大时梯度收敛的较快,当a过大时可能无法收敛,比如x减去一个很小的负值,函数值比原来距离正确的最小值点更远了。可见对于这样一个平滑的凸函数,迭代的步子会随着次数增加越迈越小,原因就是导数越来越小了。这样就会使得x逐渐逼近最小值点。
对于神经网络的cost function,它不仅仅有一个参数,我们便需要求出cost function对每个参数的偏导数,在最后统一进行参数更新后进行下一轮迭代。
神经网络系统使用正向传播求当前参数的损失,然后反向传播回传误差,根据误差信号迭代修正每层的权重。SGD算法(stochastic gradient descent)的第一步是随机初始化每一个参数。Stochastic的意思正是随机。通过这组随机的参数计算得到每一个神经元的输入输出值和损失函数后,就可以求损失函数对各个参数的偏导数了,梯度更新的那个delta就等于alpha*偏导数。偏导数怎么求就不多说了,高中数学喽。
而BP算法则是用来求那一堆偏导数的,BP的意思是反向传播。就是把最后一层的误差反向传递回别的神经元,得到每一层的误差函数,从而解出偏导数。
我们定义(delta^{(l)}_j)为第l层,节点j的误差
对于输出层(第四层)
(delta^{(4)}=a^{(4)}-y),这里当然每一个都是3维的向量
往前传递:
(delta^{(3)}=((Theta^{(3)})^Tdelta^{(4)}).*g^{'}(z^{(3)}))
(delta^{(2)}=((Theta^{(2)})^Tdelta^{(3)}).*g^{'}(z^{(2)}))
则损失函数对于每个参数的偏导数为:
(dfrac{partial J(Theta)}{partial Theta_{i,j}^{(l)}} = frac{1}{m}sum_{t=1}^m a_j^{(t)(l)} {delta}_i^{(t)(l+1)})
这个东西的证明出奇的复杂,有兴趣的可以谷歌一下,当每一个偏导数都求出来后,就可以套用上边的梯度下降算法迭代出来最佳的参数组合喽。这就是神经网络。
好了,上边的例子就是一个图像分类的问题demo,差不多说的很清楚了吧。然后考虑一下实际的图像分类问题,会遇到哪些问题呢?
首先图像的分辨率不能是9像素了,这能看出来啥啊,然后就是图像的类别,也不能就3类了,这个新球上的图片还是有个几千个类别的吧,这样就会遇到一些计算上的问题,比如图片的分辨率是1080p,那么输入维度就是1980*1200=2376000,通常隐层节点数量要大于输入维度,而隐层层数也随着分类问题的复杂而提高,就算一个图像分类神经网络的隐层节点数量和输入维度一致,那传递参数W维度就成了。。。200w*200w=2万亿个了。。。这么大的数据量,老黄也没辙,只能优化算法。
关于深度的神经网络为何难以训练有很多细节,可以推荐一本在线书:
http://neuralnetworksanddeeplearning.com/chap5.html
#我还没看完。。
写到这里深刻感觉到关于深度神经网络的知识量还是很大的,这里只做知识结构梳理和重要的key point描述。其实对于此类知识,我个人的看法是掌握原理即可move on,需要其中的细节再去查看资料,对每一个细节都详细证明是有一些浪费时间的,对于初学者(just like me)来说,很快的了解并将这个技术应用到一个测试平台上是更重要的,其次是紧跟潮流看看最新的进展是在研究什么。数学很重要,但它只是工具罢了。我们要掌握的是如何用数学解决问题。
具体怎么搞?
卷积神经网络