网络流相关知识点以及题目//POJ1273 POJ 3436 POJ2112 POJ 1149

首先来认识一下网络流中最大流的问题

给定一个有向图G＝（V，E），把图中的边看做成管道，边权看做成每根管道能通过的最大流量（容量），给定源点s和汇点t，在源点有一个水源，在汇点有一个蓄水池，问s－t的最大水流量是多少

网络流图里,源点流出的量等于汇点流入的量,除源汇外的任何点,其流入量之和等于流出量之和。

首先我们来看下面的图

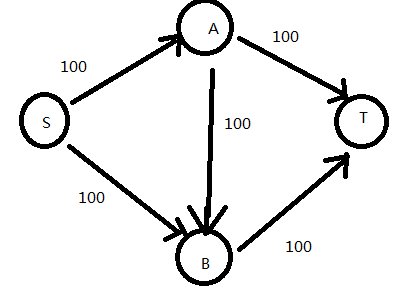
s是源点,t是汇点

先这么想,先用dfs找出一条从s-t的路线,把他塞满,然后流量就是路径中容量最小的那条路的容量,然后把路径上的容量都剪去这个流量,再重新从s-t找可行路径,直到找不到为止

用这种思路看这个图

先走S-A-B-T,这样流量为100,并且没有可行路径了,即操作结束.

可是很明显,从S-A-T,S-B-T这两条路加起来的流量为200。所以这种思路是错的。

主要是过早的认为A-B的流量不为0

改进的思路：建立一个可以修改的网络，使得不合理的流可以被删掉

一种实现：对上次dfs时找到的流量路径上的边，添加一条“反向”边，反向边上的容量等于上次dfs时找到的该边上的流量，然后再利用“反向”的容量和其他边上剩余的容量寻找路径。

使用这种思路再求一次

第一次dfs后

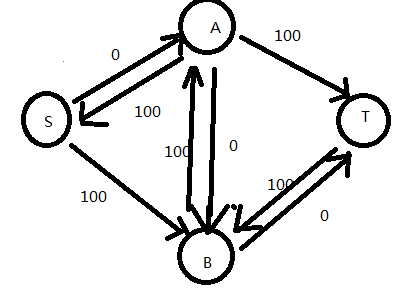
第二次dfs（为了方便把容量为0的边删了）

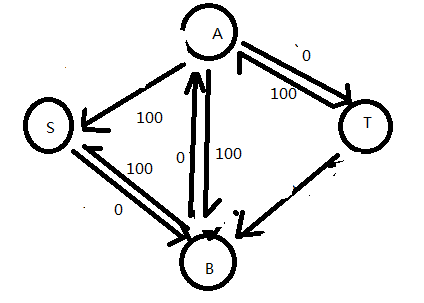
这个时候已经没有可以走的边了，流量为200，dfs结束

为什么这种思路是正确的呢，网上有不少详细的证明。

Ford-Fulkerson算法
就是用这种思路做的

用dfs求增广路径，每次找到之后处理，直到找不到为止。

假设有n个定点，m条边，那么dfs的复杂度为n+m；

dfs运行c次

所以复杂度为c*(n+m);

但是dfs可能会运行很多次。

比如上面的图如果A-B中有条容量为1的边，那么运气不好的话，能执行200次dfs；

但实际上只要用2次就能找到

在每次增广的时候，选择从源到汇的具有最少边数的增广路径,即不是通过dfs寻找增广路径，而是通过bfs寻找增广路径。
这就是Edmonds-Karp 最短增广路算法
已经证明这种算法的复杂度上限为nm2 (n是点数， m是边数）；

现在来说几道题目

1-〉POJ 1273

题意:网络流的裸题，1为源点，n为汇点，给定每条边的容量，求最大流，用EK算法

1273

Accepted

1052K

0MS

G++

1430B

 1 #include <stdio.h>
 2 #include <iostream>
 3 #include <stdlib.h>
 4 #include <string.h>
 5 #include <algorithm>
 6 #include <vector>
 7 #include <queue>
 8 using namespace std;
 9 #define N 300
10 #define INF 0x7fffffff
11 int Map[N][N];
12 int path[N];
13 //bool vis[N];
14 int n,m;
15 bool bfs(int s,int t)
16 {
17     int p;
18     queue<int> q;
19     memset(path,-1,sizeof(path));
20    //memset(vis,false,sizeof(vis));
21     path[s]=s;
22    // vis[s]=true;
23     q.push(s);
24     while(!q.empty())
25     {
26         p=q.front();
27         q.pop();
28         for(int i=1;i<=n;i++)
29         {
30             if(Map[p][i]>0&&path[i]==-1)
31             {
32                 path[i]=p;
33                 //vis[i]=true;
34                 if(i==t)
35                     return true;
36                 q.push(i);
37             }
38         }
39     }
40     return false;
41 }
42 int EK(int s,int t)
43 {
44     int flow=0;
45     int d;
46     int i;
47     while(bfs(s,t))
48     {
49         d=INF;
50         for(i=t;i!=s;i=path[i])
51         {
52             d=min(d,Map[path[i]][i]);
53         }
54         for(i=t;i!=s;i=path[i])
55         {
56             Map[path[i]][i]-=d;
57             Map[i][path[i]]+=d;
58         }
59         flow+=d;
60     }
61     return flow;
62 }
63 int main()
64 {
65     while(scanf("%d %d",&m,&n)!=EOF)
66     {
67         memset(Map,0,sizeof(Map));
68         for(int i=1;i<=m;i++)
69         {
70             int from,to,flow;
71             scanf("%d %d %d",&from,&to,&flow);
72             Map[from][to]+=flow;
73         }
74         printf("%d
",EK(1,n));
75     }
76     
77     return 0;
78 }

View Code

2-〉POJ 3436

题意：一台电脑有P个部分，当电脑所有部分都被修好的时候，这台电脑才能出厂，有N台机器，每台机器每天最多能处理Q台电脑，机器只能接收与要求相符合的电脑，0表示这个部件不能有，1表示这个部件必须有，2表示这个部件可有可无，机器接受电脑部件之后会产出相应的产品，1表示这个部件有，0表示这个部件没有。求工厂一天能出厂多少台电脑。

思路：拆点建图，把接收形如222，000。。。（只要其中没有1），就把源点向这个点连一条容量为无穷大的边，把产出为111的，就把这个点向汇点连一条无穷大的边，我把编号为i的点，那么这个点拆成2*i-1和2*i两个点，2*i-1代表接受的，2*i代表产出的，这两个点之间连一条容量为第i台机器每天处理的电脑量的边，如果某台机器产出的点符合令一台机器接受的点，那就把那两个点也连上一条容量为无穷大的边。之后求最大流就可以了。

3436

Accepted

8648K

32MS

G++

3338B

  1 #include <stdio.h>
  2 #include <string.h>
  3 #include <iostream>
  4 #include <queue>
  5 #include <stdlib.h>
  6 #include <stack>
  7 using namespace std;
  8 #define N 1000
  9 #define INF 0x7fffffff
 10 int pre[N];
 11 int map[N][N];
 12 int mmap[N][N];
 13 int P,n;
 14 struct node
 15 {
 16     int rec[N];
 17     int pro[N];
 18     int flow;
 19 };
 20 node mac[N];
 21 bool bfs(int s,int t)
 22 {
 23     int p;
 24     stack<int> q;//不知道为什么stack能过queue就wa了。。
 25     memset(pre,-1,sizeof(pre));
 26     pre[s]=s;
 27     q.push(s);
 28     while(!q.empty())
 29     {
 30         p=q.top();
 31         q.pop();
 32         for(int i=0;i<=2*n+1;i++)
 33         {
 34             if(map[p][i]>0&&pre[i]==-1)
 35             {
 36                 pre[i]=p;
 37                 if(i==t)
 38                     return true;
 39                 q.push(i);
 40                 
 41             }
 42         }
 43     }
 44     return false;
 45 }
 46 void EK(int s,int t)
 47 {
 48     int flow=0;
 49     int d,i;
 50     int cnt=0;
 51     while(bfs(s,t))
 52     {
 53         d=INF;
 54         for(i=t;i!=s;i=pre[i])
 55             d=min(d,map[pre[i]][i]);
 56         for(i=t;i!=s;i=pre[i])
 57         {
 58             map[pre[i]][i]-=d;
 59             if(!mmap[pre[i]][i])
 60             {
 61                 if(pre[i]%2==0&&i&1&&i!=t&&pre[i]!=0)
 62                 {
 63                     
 64                     cnt++;
 65                 }
 66             }
 67             map[i][pre[i]]+=d;
 68             mmap[pre[i]][i]+=d;//每台机器之间流过的电脑数量
 69         }
 70         
 71         flow+=d;
 72     }
 73     printf("%d %d
",flow,cnt);//最大流就是最多能产出的电脑，cnt就是几条机器之间的路径
 74     for(int i=1;i<=2*n;i++)
 75         for(int j=1;j<=2*n;j++)
 76         {
 77             if(mmap[i][j]&&i%2==0&&j%2!=0)
 78             {
 79                 printf("%d %d %d
",i/2,(j+1)/2,mmap[i][j]);
 80             }
 81         }
 82 }
 83 int main()
 84 {
 85     while(scanf("%d %d",&P,&n)!=EOF)
 86     {
 87         int cnt=1;
 88         memset(map,0,sizeof(map));
 89         memset(mmap,0,sizeof(mmap));
 90         for(int i=1;i<=n;i++)
 91         {
 92             scanf("%d",&mac[i].flow);
 93             for(int j=1;j<=P;j++)scanf("%d",&mac[i].rec[j]);
 94             for(int j=1;j<=P;j++)scanf("%d",&mac[i].pro[j]);
 95             map[cnt][cnt+1]=mac[i].flow;//拆点
 96             cnt+=2;
 97         }
 98         bool flag;
 99         for(int i=1;i<=n;i++)//处理源点和汇点
100         {
101             bool flag1=true;
102             bool flag2=true;
103             for(int j=1;j<=P;j++)
104                 if(mac[i].pro[j]==0)flag2=false;
105             if(flag2)
106                 map[i*2][2*n+1]=INF;
107             flag1=true;
108             flag2=true;
109             for(int j=1;j<=P;j++)
110                 if(mac[i].rec[j]==1)flag1=false;
111             if(flag1)
112                 map[0][2*i-1]=INF;
113         }
114         for(int i=1;i<=n;i++)//每台机器之间连边
115         {
116             for(int j=1;j<=n;j++)
117             {
118                 if(i==j)
119                     continue;
120                 for(int k=1;k<=P;k++)
121                 {
122                     flag=true;
123                     if((mac[i].pro[k]==1&&mac[j].rec[k]==0)||(mac[i].pro[k]==0&&mac[j].rec[k]==1))
124                     {
125                         flag=false;
126                         break;
127                     }
128                 }
129                 if(flag)
130                 {
131                     int u=i*2;
132                     int v=j*2-1;
133                     map[u][v]=INF;
134                 }
135             }
136         }
137         
138        /* for(int i=0;i<=2*n+1;i++)
139         {
140             for(int j=0;j<=2*n+1;j++)
141             {
142                 printf("i:%d j:%d map[i][j]=%d
",i,j,map[i][j]);
143             }
144         }*/
145         EK(0,2*n+1);
146     }
147     return 0;
148 }

View Code

3-> POJ 2112

题意：有k个挤奶机编号为1-k，有c个奶牛编号为k＋1-k+c，奶牛和挤奶机之间有路径（没有路径给出来的距离是0），一个挤奶机每天可以处理M头奶牛
求出需要走最大距离去挤奶的牛的路径最小值
思路：先用floyd求出每个牛到每个挤奶机的最小路径，问题就转化成了已知每个奶牛到每个挤奶机的路径，一个奶牛只能去一台机器，每台机器每天可以处理M头牛，求需要走最大距离去挤奶的牛的路径的最小值，用网络流＋二分答案，先假设最远的距离是求floyd时所求得的最短路径中的最大值，把源点和每头牛之间连容量为1的一条边，把每个挤奶器与汇点连容量为M的一条边，每头牛到挤奶机的距离如果小于或者等于dismax说明可以连接一条容量为1的边，然后求最大流，如果最大流等于C即牛的数量的时候，二分答案，直到求出答案为止。

2112

Accepted

5528K

750MS

G++

2883B

  1 #include <stdio.h>
  2 #include <string.h>
  3 #include <stdlib.h>
  4 #include <iostream>
  5 #include <algorithm>
  6 #include <queue>
  7 #include <stack>
  8 #define N 1000
  9 #define INF 999999999
 10 using namespace std;
 11 int mmap[N][N];
 12 int n;
 13 int k,c,m;
 14 int map[N][N];
 15 int pre[N];
 16 int maxn;
 17 int dismaxn;
 18 void floyd()
 19 {
 20    
 21     maxn=-1;
 22     //for(int i=k+1;i<=n;i++)
 23        // for(int j=1;j<=k;j++)
 24             //cout<<"i:"<<i<<" j:"<<j<<" mmap[i][j]:"<<mmap[i][j]<<endl;
 25     for(int k=1;k<=n;k++)
 26     {
 27         for(int i=1;i<=n;i++)
 28         {
 29             for(int j=1;j<=n;j++)
 30             {
 31                 mmap[i][j]=min(mmap[i][j],mmap[i][k]+mmap[k][j]);//保留原图
 32                 
 33             }
 34         }
 35     }
 36     for(int i=k+1;i<=n;i++)
 37         for(int j=1;j<=k;j++)
 38             maxn=max(maxn,mmap[i][j]);//二分答案的上界
 39  
 40     dismaxn=maxn;
 41 }
 42 void build(int dismax)
 43 {
 44     memset(map,0,sizeof(map));
 45     
 46     for(int i=k+1;i<=n;i++)
 47     {
 48         for(int j=1;j<=k;j++)
 49         {
 50             
 51             if(mmap[i][j]<=dismax)
 52             {
 53                 map[i][j]=1;//建边
 54                 
 55             }
 56         }
 57     }
 58     for(int i=k+1;i<=n;i++)
 59     {
 60         map[0][i]=1;
 61         
 62     }
 63     for(int i=1;i<=k;i++)
 64     {
 65         map[i][n+1]=m;
 66         
 67     }
 68 }
 69 bool bfs(int s,int t)//寻找增广路径
 70 {
 71     int p;
 72     queue<int> q;
 73     memset(pre,-1,sizeof(pre));
 74     pre[s]=s;
 75     q.push(s);
 76     while(!q.empty())
 77     {
 78         p=q.front();
 79         q.pop();
 80         for(int i=1;i<=n+1;i++)
 81         {
 82     
 83             if(map[p][i]>0&&pre[i]==-1)
 84             {
 85                 pre[i]=p;
 86                     if(i==t)
 87                     return true;
 88                 q.push(i);
 89             }
 90         }
 91     }
 92     return false;
 93 }
 94 bool ek(int s,int t)
 95 {
 96     int flow=0,d,i;
 97   
 98     while(bfs(s,t))
 99     {
100         d=INF;
101         for(i=t;i!=s;i=pre[i])
102             d=min(d,map[pre[i]][i]);
103         for(i=t;i!=s;i=pre[i])
104         {
105             map[pre[i]][i]-=d;
106             map[i][pre[i]]+=d;
107         }
108         flow+=d;
109     }
110     if(flow==c)
111         return true;
112     return false;
113 }
114 void bound()
115 {
116     int ub=maxn;
117     int lb=0;
118     while(ub-lb>1)
119     {
120         int mid=(lb+ub)/2;
121         build(mid);
122         if(ek(0,n+1))
123         {
124             ub=mid;
125         }
126         else lb=mid;
127     }
128     printf("%d
",ub);
129 }
130 int main()
131 {
132     while(scanf("%d %d %d",&k,&c,&m)!=EOF)
133     {
134         n=k+c;
135         for(int i=1;i<=n;i++)
136         {
137             for(int j=1;j<=n;j++)
138             {
139                 scanf("%d",&mmap[i][j]);
140                 if(mmap[i][j]==0)
141                     mmap[i][j]=INF;
142             }
143         }
144         
145         floyd();
146         bound();
147     }
148 return 0;
149  }

View Code

4->POJ 1149

题意：有M个锁着的猪圈，每个猪圈有对应的猪的数量，每个猪圈能容纳无穷多的猪，Mirko没有猪圈的钥匙，顾客一个接着一个去农场买猪，每个顾客都有相应猪圈的钥匙和想买猪的数量，每次顾客打开猪圈之后，打开的猪圈里面的猪可以去任意打开的猪圈，要求出来每天能卖的最多的猪

思路：这题的建图有点麻烦，先按照样例建一个图

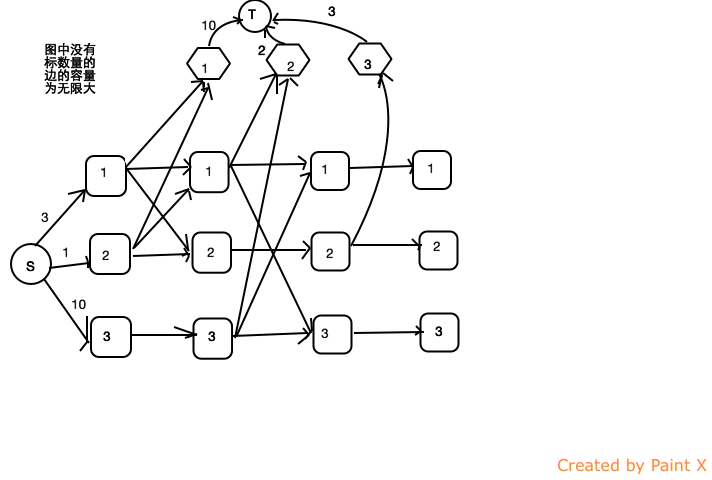
就算知道这题是求最大流的题目但是拿着这个图也写不了吧。。。

但是图是可以简化的

点的合并有这些规律

规律 1. 如果几个节点的流量的来源完全相同，则可以合并成一个

规律 2. 如果几个节点的流量的去向完全相同, 则可以把它们合并成一个。

规律 3. 如果从点 u 到点 v 有一条容量为 +∞ 的边,并且 u 是 v 的唯一流量来源,或者 v 是 u 的唯一流量去向,则可以把 u 和 v 合并成一个节点。

简化完之后的图

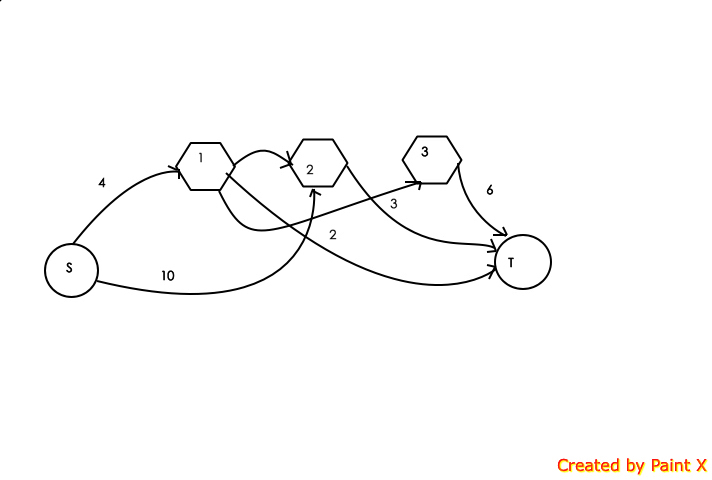
其实可以这么想这个图，每个猪圈的第一个顾客，就把这个猪圈就把源点向顾客连一条边，边的容量就是猪圈里面猪的数量，因为他是猪圈的第一个顾客，所以初始猪圈里面的猪他都能买，他打开了猪圈M之后，可能他打开的猪圈里面所有的猪都置换进了M里面，而M里面的猪可能又会被M的下一位顾客买走，所以对每个猪圈里面的1－n个用户，把i－>i+1连一条容量为无穷大的边

所以每次如果想不到什么好的构图方法的话，可以先根据样例把图画出来，然后利用简化的规则，把图简化一下，说不定就有建图的思路了。

1149

Accepted

1388K

47MS

G++

2198B

  1 #include <stdio.h>
  2 #include <string.h>
  3 #include <stdlib.h>
  4 #include <iostream>
  5 #include <algorithm>
  6 #include <queue>
  7 #include <vector>
  8 #include <stack>
  9 #define N 200
 10 #define INF 999999999
 11 using namespace std;
 12 int n,m;
 13 struct node
 14 {
 15     int key[2000];
 16     int cnt;
 17     int need;
 18 };
 19 node peo[N];
 20 int pre[N*N];
 21 int map[N][N];
 22 int pig[N*10];
 23 bool vis[N*10];
 24 vector<int> user[N*10];
 25 void build()//建图
 26 {
 27     for(int i=1;i<=m;i++)
 28     {
 29         for(int j=0;j<user[i].size()-1;j++)
 30         {
 31             map[user[i][j]][user[i][j+1]]=INF;
 32         }
 33     }
 34     
 35 }
 36 bool bfs(int s,int t)
 37 {
 38     memset(pre,-1,sizeof(pre));
 39    /* for(int i=0;i<=n+1;i++)
 40         for(int j=0;j<=n+1;j++)
 41             cout<<"i:"<<i<<"j:"<<j<<"map[i][j] "<<map[i][j]<<endl;*/
 42     queue<int> q;
 43     q.push(s);
 44     pre[s]=s;
 45     while(!q.empty())
 46     {
 47         int p=q.front();
 48         q.pop();
 49         for(int i=1;i<=n+1;i++)
 50         {
 51             if(map[p][i]>0&&pre[i]==-1)
 52             {
 53                 pre[i]=p;
 54                 if(i==t)
 55                     return true;
 56                 q.push(i);
 57             }
 58             
 59         }
 60     }
 61     return false;
 62 }
 63 int EK(int s,int t)
 64 {
 65     int d,flow=0;
 66     while(bfs(s,t))
 67     {
 68         d=INF;
 69         for(int i=t;i!=s;i=pre[i])
 70             d=min(d,map[pre[i]][i]);
 71         for(int i=t;i!=s;i=pre[i])
 72         {
 73             map[pre[i]][i]-=d;
 74             map[i][pre[i]]+=d;
 75            
 76         }
 77         flow+=d;
 78     }
 79     return flow;
 80 }
 81 int main()
 82 {
 83     while(scanf("%d %d",&m,&n)!=EOF)
 84     {
 85         for(int i=1;i<=m;i++)
 86             scanf("%d",&pig[i]);
 87         memset(vis,false,sizeof(vis));
 88         for(int i=1;i<=n;i++)
 89         {
 90             scanf("%d",&peo[i].cnt);
 91             for(int j=1;j<=peo[i].cnt;j++)
 92             {
 93                 scanf("%d",&peo[i].key[j]);
 94                 user[peo[i].key[j]].push_back(i);//每个猪圈按照顺序把顾客编号放进去
 95                 if(!vis[peo[i].key[j]])//给第一个顾客连线
 96                 {
 97                     map[0][i]+=pig[peo[i].key[j]];
 98                     vis[peo[i].key[j]]=true;
 99                 }
100             }
101             scanf("%d",&peo[i].need);
102             map[i][n+1]=peo[i].need;//顾客和汇点连线
103         }
104         build();//建图
105         printf("%d
",EK(0,n+1));
106     }
107     return 0;
108 }

View Code

相关阅读:
idea 从svn导入项目遇到的错误
 用sql语句处理字符串以逗号截开分别获取值
 tree grid 实现编辑保存然后整体存入数据库
 EasyUI的TreeGrid的json格式,树状图显示问题
 vue.js--菜鸟级入门
 Django3.0知识笔记——WSGI&ASGI是什么？
open stack
shell脚本简介及常用文本编辑命令
 shell脚本之变量与运算符
 shell编程之流程控制（for、while、case、break、continue）
原文地址：https://www.cnblogs.com/as3asddd/p/5410693.html