2020牛客多校第九场B- Groundhog and Apple Tree

https://ac.nowcoder.com/acm/contest/5674/B

题意

现在有一棵树，你要从1开始跳一遍所有的点并且每条边只能走两次，再回到1，每条边都有一个边权，你走过这条边会先消耗(w_i)点HP，每个点都有一个果子，吃掉这个果子会上升(a_i)点HP，你在任何时候的HP不能小于0.并且你如果休息一秒钟会恢复1点HP。问你最少要休息多少时间才能走完这棵树。

题解

设(f[u])为遍历完子树增加多少体力，(g[u])表示体力为0遍历完子树最低减少到多少

那么最后答案显然为(min(0, -g[1]))

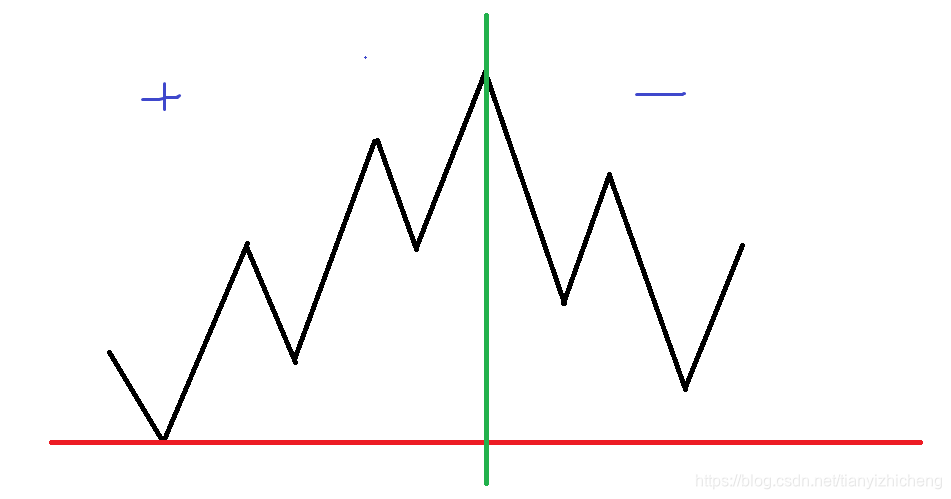
考虑这张图，绿线左边的是增加体力为正的情况，显然要g大的的排在前面，这样保证最低点最高，对于绿线右边，可以想到，我们需要的是最低点低的，且增加体力相对多的排在前面，所以按f-g排序，按树形dp转移即可

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
struct READ {
    inline char read() {
    #ifdef _WIN32
        return getchar();
    #endif
        static const int IN_LEN = 1 << 18 | 1;
        static char buf[IN_LEN], *s, *t;
        return (s == t) && (t = (s = buf) + fread(buf, 1, IN_LEN, stdin)), s == t ? -1 : *s++;
    }
    template <typename _Tp> inline READ & operator >> (_Tp&x) {
        static char c11, boo;
        for(c11 = read(),boo = 0; !isdigit(c11); c11 = read()) {
            if(c11 == -1) return *this;
            boo |= c11 == '-';
        }
        for(x = 0; isdigit(c11); c11 = read()) x = x * 10 + (c11 ^ '0');
        boo && (x = -x);
        return *this;
    }
} in;

const int N = 1e5 + 50;
int a[N];
struct node {
    int v, w;
    node(int v = 0, int w = 0): v(v), w(w) {}
};
vector<node> G[N];
ll f[N], g[N];//f遍历完子树增加多少体力，g体力为0遍历完子树最低减少到多少
struct S1 {
    ll x, y;
    bool operator < (const S1 &b) const {
        return y > b.y;
    } 
};
struct S2 {
    ll x, y;
    bool operator < (const S2 &b) const {
        return x - y > b.x - b.y;
    }
};

void dfs(int u, int fa) {
    for (node e : G[u]) {
        if (e.v == fa) continue;
        dfs(e.v, u);
    }
    vector<S1> s1; vector<S2> s2;
    for (node e : G[u]) {
        if (e.v == fa) continue;
        f[e.v] -= 2ll * e.w;
        g[e.v] -= e.w;
        g[e.v] = min(g[e.v], (ll)-e.w);
        g[e.v] = min(g[e.v], f[e.v]);
        if (f[e.v] >= 0) s1.push_back({f[e.v], g[e.v]});
        else s2.push_back({f[e.v], g[e.v]});
    }
    sort(s1.begin(), s1.end()); sort(s2.begin(), s2.end());
    for (auto e : s1) {
        g[u] = min(g[u], e.y + f[u]);
        f[u] += e.x;
    }
    for (auto e : s2) {
        g[u] = min(g[u], e.y + f[u]);
        f[u] += e.x;
    }
    f[u] += a[u]; g[u] += a[u];
}
void solve() {
    int n; in >> n;
    for (int i = 1; i <= n; i++) in >> a[i], G[i].clear(), f[i] = g[i] = 0;
    for (int i = 1; i < n; i++) {
        int u, v, w; in >> u >> v >> w;
        G[u].push_back(node(v, w));
        G[v].push_back(node(u, w));
    }
    dfs(1, 0);
    printf("%lld
", max(0ll, -g[1]));
}
int main() {
    int t; in >> t;
    while (t--) solve();
    return 0;
}