线段树进阶

Codeforces-438D The Child and Sequence

Description

At the children's day, the child came to Picks's house, and messed his house up. Picks was angry at him. A lot of important things were lost, in particular the favorite sequence of Picks.

Fortunately, Picks remembers how to repair the sequence. Initially he should create an integer array a[1], a[2], ..., a[n]. Then he should perform a sequence of m operations. An operation can be one of the following:

1. Print operation l, r. Picks should write down the value of .
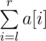2. Modulo operation l, r, x. Picks should perform assignment a[i] = a[i] mod x for each i (l ≤ i ≤ r).
3. Set operation k, x. Picks should set the value of a[k] to x (in other words perform an assignment a[k] = x).

Can you help Picks to perform the whole sequence of operations?

Input

The first line of input contains two integer: n, m (1 ≤ n, m ≤ (10^5)). The second line contains n integers, separated by space: a[1], a[2], ..., a[n] (1 ≤ a[i] ≤ $ 10^9$) — initial value of array elements.

Each of the next m lines begins with a number type .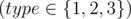

• If type = 1, there will be two integers more in the line: l, r (1 ≤ l ≤ r ≤ n), which correspond the operation 1.
• If type = 2, there will be three integers more in the line: l, r, x (1 ≤ l ≤ r ≤ n; 1 ≤ x ≤ 109), which correspond the operation 2.
• If type = 3, there will be two integers more in the line: k, x (1 ≤ k ≤ n; 1 ≤ x ≤ 109), which correspond the operation 3.

Output

For each operation 1, please print a line containing the answer. Notice that the answer may exceed the 32-bit integer.

Examples

Input

5 5
1 2 3 4 5
2 3 5 4
3 3 5
1 2 5
2 1 3 3
1 1 3

Output

8
5

Input

10 10
6 9 6 7 6 1 10 10 9 5
1 3 9
2 7 10 9
2 5 10 8
1 4 7
3 3 7
2 7 9 9
1 2 4
1 6 6
1 5 9
3 1 10

Output

49
15
23
1
9

Note

Consider the first testcase:

• At first, a = {1, 2, 3, 4, 5}.
• After operation 1, a = {1, 2, 3, 0, 1}.
• After operation 2, a = {1, 2, 5, 0, 1}.
• At operation 3, 2 + 5 + 0 + 1 = 8.
• After operation 4, a = {1, 2, 2, 0, 1}.
• At operation 5, 1 + 2 + 2 = 5.

题解

首先有一个结论，每次取模都会使一个数至少缩小一半，a mod x，如果x大于a / 2，则取模后的剩余则在a / 2内，若x小于a / 2，同样也在a / 2内。所以对于一个数x我们至多对其取模(logx)次，记录一下区间的最大值，如果最大值小于取模值我们就不修改，否则就暴力取模。

这种暴力取模只适用于单点修改

代码

#include <cstdio>
#include <algorithm>
#define lson (o << 1)
#define rson (o << 1 | 1)
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
ll sumv[N << 2];
ll maxv[N << 2];
void pushup(int o) {
    sumv[o] = sumv[lson] + sumv[rson];
    maxv[o] = max(maxv[lson], maxv[rson]);
}
void build(int o, int l, int r) {
    if (l == r) {
        scanf("%lld", &sumv[o]);
        maxv[o] = sumv[o];
        return;
    }
    int mid = (l + r) >> 1;
    build(lson, l, mid); build(rson, mid + 1, r);
    pushup(o);
}
void modd(int o, int l, int r, int ql, int qr, int v) {
    if (ql <= l && r <= qr) {
        if (maxv[o] < v) return;
    }
    if (l == r) {
        sumv[o] = sumv[o] % v;
        maxv[o] = maxv[o] % v;
        return;
    }
    int mid = (l + r) >> 1;
    if (ql <= mid) modd(lson, l, mid, ql, qr, v);
    if (qr > mid) modd(rson, mid + 1, r, ql, qr, v);
    pushup(o);
}
void update(int o, int l, int r, int pos, int v) {
    if (l == r) {
        sumv[o] = v;
        maxv[o] = v;
        return;
    }
    int mid = (l + r) >> 1;
    if (pos <= mid) update(lson, l, mid, pos, v);
    else update(rson, mid + 1, r, pos, v);
    pushup(o);
}
ll query(int o, int l, int r, int ql, int qr) {
    if (ql <= l && r <= qr) {
        return sumv[o];
    }
    int mid = (l + r) >> 1;
    ll ans = 0;
    if (ql <= mid) ans += query(lson, l, mid, ql, qr);
    if (qr > mid) ans += query(rson, mid + 1, r, ql, qr);
    return ans;
}
int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    build(1, 1, n);
    for (int i = 1; i <= m; i++) {
        int t;
        scanf("%d", &t);
        int l, r, k, x;
        switch(t) {
            case 1: scanf("%d%d", &l, &r); printf("%lld
", query(1, 1, n, l, r)); break;
            case 2: scanf("%d%d%d", &l, &r, &x); modd(1, 1, n, l, r, x); break;
            case 3: scanf("%d%d", &k, &x); update(1, 1, n, k, x); break;
        }
    }
}

HDU-4578 Transformation

Description

Yuanfang is puzzled with the question below:
There are n integers, a1, a2, …, an. The initial values of them are 0. There are four kinds of operations.
Operation 1: Add c to each number between ax and ay inclusive. In other words, do transformation ak<---ak+c, k = x,x+1,…,y.
Operation 2: Multiply c to each number between ax and ay inclusive. In other words, do transformation ak<---ak×c, k = x,x+1,…,y.
Operation 3: Change the numbers between ax and ay to c, inclusive. In other words, do transformation ak<---c, k = x,x+1,…,y.
Operation 4: Get the sum of p power among the numbers between ax and ay inclusive. In other words, get the result of axp+ax+1p+…+ay p.
Yuanfang has no idea of how to do it. So he wants to ask you to help him.

Input

There are no more than 10 test cases.
For each case, the first line contains two numbers n and m, meaning that there are n integers and m operations. 1 <= n, m <= 100,000.
Each the following m lines contains an operation. Operation 1 to 3 is in this format: "1 x y c" or "2 x y c" or "3 x y c". Operation 4 is in this format: "4 x y p". (1 <= x <= y <= n, 1 <= c <= 10,000, 1 <= p <= 3)
The input ends with 0 0.

Output

For each operation 4, output a single integer in one line representing the result. The answer may be quite large. You just need to calculate the remainder of the answer when divided by 10007

Sample Input

5 5
3 3 5 7
1 2 4 4
4 1 5 2
2 2 5 8
4 3 5 3
0 0

Sample Output

307
7489

题解

线段树同时维护三种标记，cov(覆盖)，mulv(乘)，addv(加)，下传标记时，依次下传cov，mulv，addv，下传cov时要修改mulv和addv，下传mulv时要修改addv，同时维护三个数组记录区间的1次方，2次方，3次方和，加法修改时用一次方（原来，非更新后）和推出二次方和，用一次方和二次方（原来）和推出三次方和。

代码

#include <cstdio>
#include <algorithm>
#define lson (o << 1)
#define rson (o << 1 | 1)
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
const ll p = 10007;
ll sumv[N << 2];
ll sum2v[N << 2];
ll sum3v[N << 2];
ll addv[N << 2];
ll mulv[N << 2];
ll cov[N << 2];
int n, q;
void pushup(int o) {
    sumv[o] = (sumv[lson] + sumv[rson]) % p;
    sum2v[o] = (sum2v[lson] + sum2v[rson]) % p;
    sum3v[o] = (sum3v[lson] + sum3v[rson]) % p;
}
ll pow(ll a, int b) {
	ll ans = 1;
	for (int i = 1; i <= b; i++) {
		ans = ans * a % p;
	}
	return ans % p;
}
void pushdown(int o, int l, int r) {
    if (cov[o]) {
		cov[lson] = cov[rson] = cov[o];
        mulv[lson] = mulv[rson] = 1;
        addv[lson] = addv[rson] = 0;
        int mid = (l + r) >> 1;
        sumv[lson] = cov[o] * (ll)(mid - l + 1LL) % p;
        sumv[rson] = cov[o] * (ll)(r - mid) % p;
        sum2v[lson] = pow(cov[o], 2) % p * (ll)(mid - l + 1LL) % p;
        sum2v[rson] = pow(cov[o], 2) % p * (ll)(r - mid) % p;
        sum3v[lson] = pow(cov[o], 3) % p * (ll)(mid - l + 1LL) % p;
        sum3v[rson] = pow(cov[o], 3) % p * (ll)(r - mid) % p;
        cov[o] = 0;
    }
    if (mulv[o] != 1) {
        mulv[lson] = mulv[lson] * mulv[o] % p; mulv[rson] = mulv[rson] * mulv[o] % p;
        addv[lson] = addv[lson] * mulv[o] % p; addv[rson] = addv[rson] * mulv[o] % p;
        sumv[lson] = sumv[lson] * mulv[o] % p; sumv[rson] = sumv[rson] * mulv[o] % p;
        sum2v[lson] = sum2v[lson] * pow(mulv[o], 2) % p;
        sum2v[rson] = sum2v[rson] * pow(mulv[o], 2) % p;
        sum3v[lson] = sum3v[lson] * pow(mulv[o], 3) % p;
        sum3v[rson] = sum3v[rson] * pow(mulv[o], 3) % p;
        
        mulv[o] = 1;
    }
    if (addv[o]) {
        int mid = (l + r) >> 1;
        addv[lson] = (addv[lson] + addv[o]) % p;
        addv[rson] = (addv[rson] + addv[o]) % p;
        sum3v[lson] = (sum3v[lson] + (ll)(mid - l + 1LL) * pow(addv[o], 3) % p + 3LL * pow(addv[o], 2) * sumv[lson] % p + 3LL * addv[o] * sum2v[lson] % p) % p;
        sum3v[rson] = (sum3v[rson] + (ll)(r - mid) * pow(addv[o], 3) + 3LL * pow(addv[o], 2) % p * sumv[rson] % p + 3LL * addv[o] * sum2v[rson] % p) % p;
        sum2v[lson] = (sum2v[lson] + (ll)(mid - l + 1LL) * pow(addv[o], 2) % p + 2LL * addv[o] * sumv[lson] % p) % p;
        sum2v[rson] = (sum2v[rson] + (ll)(r - mid) * pow(addv[o], 2) % p + 2LL * addv[o] * sumv[rson] % p) % p;
        sumv[lson] = (sumv[lson] + (ll)(mid - l + 1LL) * addv[o] % p) % p;
        sumv[rson] = (sumv[rson] + (ll)(r - mid) * addv[o] % p) % p;
        addv[o] = 0;
    }
}
void build(int o, int l, int r) {
    if (l == r) {
        sumv[o] = sum2v[o] = sum3v[o] = 0;
        mulv[o] = 1;
        addv[o] = 0;
        cov[o] = 0;
        return;
    }
    sumv[o] = sum2v[o] = sum3v[o] = 0;
    mulv[o] = 1;
    addv[o] = 0;
    cov[o] = 0;
    int mid = (l + r) >> 1;
    build(lson, l, mid); build(rson, mid + 1, r);
    pushup(o);
}
void updateplus(int o, int l, int r, int ql, int qr, ll v) {
    if (ql <= l && r <= qr) {
        addv[o] = (addv[o] + v) % p;
        sum3v[o] = (sum3v[o] + (ll)(r - l + 1LL) * pow(v, 3) % p + 3LL * pow(v, 2) * sumv[o] % p + 3LL * v % p * sum2v[o] % p) % p;
        sum2v[o] = (sum2v[o] + (ll)(r - l + 1LL) * pow(v, 2) % p + 2LL * v * sumv[o] % p) % p;
        sumv[o] = (sumv[o] + (ll)(r - l + 1LL) * v % p) % p;
        return;
    }
    int mid = (l + r) >> 1;
    pushdown(o, l, r);
    if (ql <= mid) updateplus(lson, l, mid, ql, qr, v);
    if (qr > mid) updateplus(rson, mid + 1, r, ql, qr, v);
    pushup(o);
}
void updatemul(int o, int l, int r, int ql, int qr, ll v) {
    if (ql <= l && r <= qr) {
        mulv[o] = mulv[o] * v % p;
        addv[o] = addv[o] * v % p;
        sumv[o] = sumv[o] * v % p;
        sum2v[o] = sum2v[o] * pow(v, 2) % p;
        sum3v[o] = sum3v[o] * pow(v, 3) % p;
        return;
    }
    int mid = (l + r) >> 1;
    pushdown(o, l, r);
    if (ql <= mid) updatemul(lson, l, mid, ql, qr, v);
    if (qr > mid) updatemul(rson, mid + 1, r, ql, qr, v);
    pushup(o);
}
void updatecov(int o, int l, int r, int ql, int qr, ll v) {
    if (ql <= l && r <= qr) {
        mulv[o] = 1;
        addv[o] = 0;
        cov[o] = v;
        sumv[o] = v * (ll)(r - l + 1LL) % p;
        sum2v[o] = pow(v, 2) * (ll)(r - l + 1LL) % p;
        sum3v[o] = pow(v, 3) * (ll)(r - l + 1LL) % p;
        return;
    }
    int mid = (l + r) >> 1;
    pushdown(o, l, r);
    if (ql <= mid) updatecov(lson, l, mid, ql, qr, v);
    if (qr > mid) updatecov(rson, mid + 1, r, ql, qr, v);
    pushup(o);
}
ll query(int o, int l, int r, int ql, int qr, int t) {
    if (ql <= l && r <= qr) {
        if (t == 1) return sumv[o] % p;
        else if (t == 2) return sum2v[o] % p;
        else if (t == 3) return sum3v[o] % p;
    }
    int mid = (l + r) >> 1;
    pushdown(o, l, r);
    ll ans = 0;
    if (ql <= mid) ans = (ans + query(lson, l, mid, ql, qr, t)) % p;
    if (qr > mid) ans = (ans + query(rson, mid + 1, r, ql, qr, t)) % p;
    return ans % p;
}
int main() {
    while (scanf("%d%d", &n, &q)) {
        if (n == 0 && q == 0) break;
        build(1, 1, n);
        for (int i = 1; i <= q; i++) {
            int t;
            scanf("%d", &t);
            int l, r, k;
            ll c;
            switch(t) {
                case 1: scanf("%d%d%lld", &l, &r, &c); updateplus(1, 1, n, l, r, c); break;
                case 2: scanf("%d%d%lld", &l, &r, &c); updatemul(1, 1, n, l, r, c); break;
                case 3: scanf("%d%d%lld", &l, &r, &c); updatecov(1, 1, n, l, r, c); break;
                case 4: scanf("%d%d%d", &l, &r, &k); printf("%lld
", query(1, 1, n, l, r, k)); break;
            }
        }

    }
    return 0;
}

BZOJ-1018 堵塞的交通

Description

　　有一天，由于某种穿越现象作用，你来到了传说中的小人国。小人国的布局非常奇特，整个国家的交通系统可以被看成是一个2行C列的矩形网格，网格上的每个点代表一个城市，相邻的城市之间有一条道路，所以总共有2C个城市和3C-2条道路。 小人国的交通状况非常槽糕。有的时候由于交通堵塞，两座城市之间的道路会变得不连通，直到拥堵解决，道路才会恢复畅通。初来咋到的你决心毛遂自荐到交通部某份差事，部长听说你来自一个科技高度发达的世界，喜出望外地要求你编写一个查询应答系统，以挽救已经病入膏肓的小人国交通系统。 小人国的交通部将提供一些交通信息给你，你的任务是根据当前的交通情况回答查询的问题。交通信息可以分为以下几种格式：

Close r1 c1 r2 c2：相邻的两座城市(r1,c1)和(r2,c2)之间的道路被堵塞了；

Open r1 c1 r2 c2：相邻的两座城市(r1,c1)和(r2,c2)之间的道路被疏通了；

Ask r1 c1 r2 c2：询问城市(r1,c1)和(r2,c2)是否连通。如果存在一条路径使得这两条城市连通，则返回Y，否则返回N；

Input

　　第一行只有一个整数C，表示网格的列数。接下来若干行，每行为一条交通信息，以单独的一行“Exit”作为结束。我们假设在一开始所有的道路都是堵塞的。我们保证 C小于等于100000，信息条数小于等于100000。

Output

　　对于每个查询，输出一个“Y”或“N”

Sample Input

2
Open 1 1 1 2
Open 1 2 2 2
Ask 1 1 2 2
Ask 2 1 2 2
Exit

Sample Output

Y
N

题解

用线段树维护区间联通性

每个节点表示区间[s,t]的矩形

并且记录8个变量：U,D,l,r,u,d,p,q。

​ mid为(s+t)/2：

　　U：第一行mid,mid+1两列之间是否联通

　　D：第二行mid,mid+1两列之间是否联通

　　l： A,C是否联通

　　r： B,D是否联通

　　u：A,B是否联通

　　d：C,D是否联通

　　q：A,D是否联通

　　p：B,C是否联通

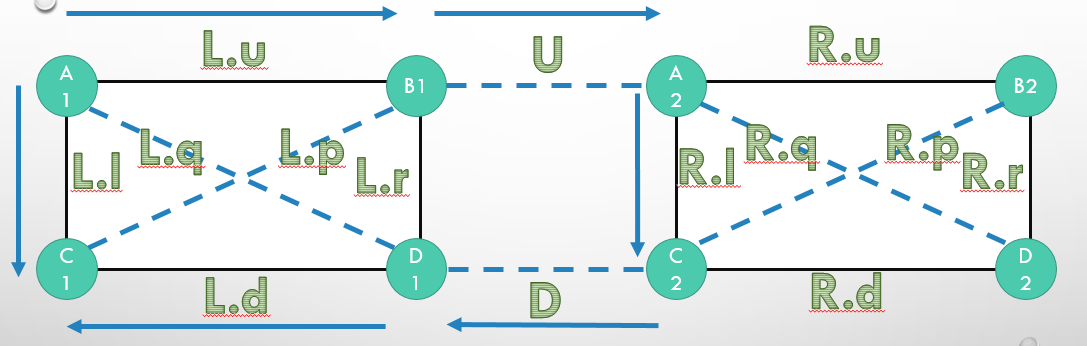
[A1, B1]为左儿子对应区间，[A2,B2]为右儿子对应区间，合并时，对应区间称为x，则

[x.l = L.l | (L.u & x.U & R.l & x.D & L.d) ]

pushup时依次维护l,r,u,d,q,p即可

查询[C1,C2]联通性时，我们要考虑先往左走，再绕回来这种情况，所以我们要同时查询[1, C1], [C1, C2], [C2,n]的联通性

代码

#include <cstdio>
#include <algorithm>
#define lson (o << 1)
#define rson (o << 1 | 1)
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
struct node {
	int l, r, u, d, q, p;
	int U, D;
} con[N << 2];
int pushup(node &o, node l, node r) {
	o.l = l.l | (l.u & o.U & r.l & o.D & l.d);
	o.r = r.r | (r.u & o.U & l.r & o.D & r.d);
	o.u = (l.u & o.U & r.u) | (l.q & o.D & r.p);
	o.d = (l.d & o.D & r.d) | (l.p & o.U & r.q);
	o.q = (l.q & o.D & r.d) | (l.u & o.U & r.q);
	o.p = (l.p & o.U & r.u) | (l.d & o.D & r.p);
}
void build(int o, int l, int r) {
	if (l == r) {
		con[o].u = con[o].d = 1;
		con[o].U = con[o].D = 1;
		return;
	}
	int mid = (l + r) >> 1;
	build(lson, l, mid); build(rson, mid + 1, r);
}
void updater(int o, int l, int r, int flag, int pos, int v) {
	int mid = (l + r) >> 1;
	if (mid == pos) {
		if (flag == 1) con[o].U = v;
		else con[o].D = v;
		pushup(con[o], con[lson], con[rson]);
		return;
	}
	if (pos <= mid) updater(lson, l, mid, flag, pos, v);
	else updater(rson, mid + 1, r, flag, pos, v);
	pushup(con[o], con[lson], con[rson]);
}
void updatec(int o, int l, int r, int pos, int v) {
	if (l == r) {
		con[o].l = con[o].r = v;
		con[o].p = con[o].q = v;
		return;
	}
	int mid = (l + r) >> 1;
	if (pos <= mid) updatec(lson, l, mid, pos, v);
	else updatec(rson, mid + 1, r, pos, v);
	pushup(con[o], con[lson], con[rson]);
}
node query(int o, int l, int r, int ql, int qr) {
	if (ql <= l && r <= qr) {
		return con[o];
	}
	int mid = (l + r) >> 1;
	if (qr <= mid) return query(lson, l, mid, ql, qr);
	else if (ql > mid) return query(rson, mid + 1, r, ql, qr);
	else {
		node ans = con[o];
		pushup(ans, query(lson, l, mid, ql, qr), query(rson, mid + 1, r, ql, qr));
		return ans;
	}
}
int main() {
	int c;
	scanf("%d", &c);
	build(1, 1, c);
	char ch[10];
	while (scanf("%s", ch)) {
		if (ch[0] == 'E') break;
		int r1, c1, r2, c2;
		scanf("%d%d%d%d", &r1, &c1, &r2, &c2);
		if (c1 > c2) {
			swap(c1, c2);
			swap(r1, r2);
		}
		if (ch[0] == 'O') {
			if (r1 == r2) updater(1, 1, c, r1, c1, 1);
			else updatec(1, 1, c, c1, 1);
		}
		if (ch[0] == 'C') {
			if (r1 == r2) updater(1, 1, c, r1, c1, 0);
			else updatec(1, 1, c, c1, 0);
		}
		if (ch[0] == 'A') {
			node pre = query(1, 1, c, 1, c1), now = query(1, 1, c, c1, c2), last = query(1, 1, c, c2, c);
			bool flag;
			if (r1 == 1 && r2 == 1) flag = now.u | (now.d & pre.r & last.l) | (now.q & last.l) | (pre.r & now.p);
			if (r1 == 2 && r2 == 2) flag = now.d | (now.u & pre.r & last.l) | (now.p * last.l) | (now.q & pre.r);
			if (r1 == 1 && r2 == 2) flag = now.q | (now.u & last.l) | (now.d & pre.r) | (now.p & pre.r & last.l);
			if (r1 == 2 && r2 == 1) flag = now.p | (now.d & last.l) | (now.u & pre.r) | (pre.r & last.l & now.q);
			if (flag == 1) printf("Y
");
			else printf("N
");
		}
	}
	return 0;
}

Codeforces-786B Legacy

Description

There are n planets in their universe numbered from 1 to n. Rick is in planet number s (the earth) and he doesn't know where

By default he can not open any portal by this gun. There are q plans in the website that sells these guns. Every time you purchase a plan you can only use it once but you can purchase it again if you want to use it more.

Plans on the website have three types:

1. With a plan of this type you can open a portal from planet v to planet u.
2. With a plan of this type you can open a portal from planet v to any planet with index in range [l, r].
3. With a plan of this type you can open a portal from any planet with index in range [l, r] to planet v.

Rick doesn't known where Morty is, but Unity is going to inform him and he wants to be prepared for when he finds and start his journey immediately. So for each planet (including earth itself) he wants to know the minimum amount of money he needs to get from earth to that planet.

Input

The first line of input contains three integers n, q and s (1 ≤ n, q ≤ 105, 1 ≤ s ≤ n) — number of planets, number of plans and index of earth respectively.

The next q lines contain the plans. Each line starts with a number t, type of that plan (1 ≤ t ≤ 3). If t = 1 then it is followed by three integers v, u and w where w is the cost of that plan (1 ≤ v, u ≤ n, 1 ≤ w ≤ 109). Otherwise it is followed by four integers v, l, r and w where w is the cost of that plan (1 ≤ v ≤ n, 1 ≤ l ≤ r ≤ n, 1 ≤ w ≤ 109).

Output

In the first and only line of output print n integers separated by spaces. i-th of them should be minimum money to get from earth to i-th planet, or  - 1 if it's impossible to get to that planet.

Examples

Input

3 5 1
2 3 2 3 17
2 3 2 2 16
2 2 2 3 3
3 3 1 1 12
1 3 3 17

Output

0 28 12 

Input

4 3 1
3 4 1 3 12
2 2 3 4 10
1 2 4 16

Output

0 -1 -1 12 

Note

In the first sample testcase, Rick can purchase 4th plan once and then 2nd plan in order to get to get to planet number 2.

题解

线段树优化连边，线段树的每个节点代表一段区间，我们不妨将这个节点向区间内的每个点连一条边权为0的边，这样我们在需要由u->[l,r]连边时直接向对应线段树节点连边即可，但是我们正向边和反向边要建在不同的节点编号上，防止一个点在树上通过边权为0的边绕一圈回到自己

代码

#include <bits/stdc++.h>
#define lson (o << 1)
#define rson (o << 1 | 1)
#define pii pair<long long, long long>
using namespace std;
typedef long long ll;
const int N = 4e5 + 10;
const ll inf = 0x7ffffffffffffff;
struct node {
    int v; ll w;
    node(int v = 0, ll w = 0): v(v), w(w) {}
};
vector<node> G[N << 2];
int pos[N << 2], neg[N << 2];
int cnt;
void build(int o, int l, int r) {
    if (l == r) {
        pos[o] = neg[o] = l;
        return;
    }
    int mid = (l + r) >> 1;
    pos[o] = ++cnt; neg[o] = ++cnt;
    build(lson, l, mid); build(rson, mid + 1, r);
    G[pos[o]].push_back(node(pos[lson], 0));G[pos[o]].push_back(node(pos[rson], 0));
    G[neg[lson]].push_back(node(neg[o], 0));G[neg[rson]].push_back(node(neg[o], 0));
}
void adde1(int o, int l, int r, int ql, int qr, int v, ll w) {
    if (ql <= l && r <= qr) {
        G[v].push_back(node(pos[o], w));
        return;
    }
    int mid = (l + r) >> 1;
    if (ql <= mid) adde1(lson, l, mid, ql, qr, v, w);
    if (qr > mid) adde1(rson, mid + 1, r, ql, qr, v, w);
}
void adde2(int o, int l, int r, int ql, int qr, int v, ll w) {
    if (ql <= l && r <= qr) {
        G[neg[o]].push_back(node(v, w));
        return;
    }
    int mid = (l + r) >> 1;
    if (ql <= mid) adde2(lson, l, mid, ql, qr, v, w);
    if (qr > mid) adde2(rson, mid + 1, r, ql, qr, v, w);
}
ll d[N];
bool vis[N];
int n, q, s;
void dijkstra(int s) {
	priority_queue<pii, vector<pii>, greater<pii> > q;
	fill (d + 1, d + n * 4 + 1, inf);
	fill (vis + 1, vis + 4 * n + 1, false);
	d[s] = 0;
	q.push(make_pair(d[s], s));
	while (!q.empty()) {
		pii now = q.top(); q.pop();
		int u = now.second;
		if (vis[u]) continue;
		vis[u] = 1;
		for (int i = 0; i < G[u].size(); i++) {
			int v = G[u][i].v;
			ll w = G[u][i].w;
			if (d[v] > d[u] + w) {
				d[v] = d[u] + w;
				q.push(make_pair(d[v], v));
			}
		}
	}
}
int main() {
    //printf("%lld
", inf);
    scanf("%d%d%d", &n, &q, &s);
    cnt = n;
    build(1, 1, n);
    while (q--) {
        int t;
        scanf("%d", &t);
        if (t == 1) {
            int u, v; ll w;
            scanf("%d%d%lld", &u, &v, &w);
            G[u].push_back(node(v, w));
        }
        if (t == 2) {
            int u, l, r; ll w;
            scanf("%d%d%d%lld", &u, &l, &r, &w);
            adde1(1, 1, n, l, r, u, w);
        }
        if (t == 3) {
            int u, l, r; ll w;
            scanf("%d%d%d%lld", &u, &l, &r, &w);
            adde2(1, 1, n, l, r, u, w);
        }
    }

    dijkstra(s);
    for (int i = 1; i <= n; i++) {
        if (d[i] < inf) printf("%lld ", d[i]);
        else printf("-1 ");
    }
    return 0;
}

Codeforces-786C Till I Collapse

Description

Rick and Morty want to find MR. PBH and they can't do it alone. So they need of Mr. Meeseeks. They Have generated n Mr. Meeseeks, standing in a line numbered from 1 to n. Each of them has his own color. i-th Mr. Meeseeks' color is (a_i).

Rick and Morty are gathering their army and they want to divide Mr. Meeseeks into some squads. They don't want their squads to be too colorful, so each squad should have Mr. Meeseeks of at most k different colors. Also each squad should be a continuous subarray of Mr. Meeseeks in the line. Meaning that for each 1 ≤ i ≤ e ≤ j ≤ n, if Mr. Meeseeks number i and Mr. Meeseeks number j are in the same squad then Mr. Meeseeks number e should be in that same squad.

Also, each squad needs its own presidio, and building a presidio needs money, so they want the total number of squads to be minimized.

Rick and Morty haven't finalized the exact value of k, so in order to choose it, for each k between 1 and n (inclusive) need to know the minimum number of presidios needed.

Input

The first line of input contains a single integer n (1 ≤ n ≤ (10^5)) — number of Mr. Meeseeks.

The second line contains n integers a1, a2, ..., an separated by spaces (1 ≤ ai ≤ n) — colors of Mr. Meeseeks in order they standing in a line.

Output

In the first and only line of input print n integers separated by spaces. i-th integer should be the minimum number of presidios needed if the value of k is i.

Examples

Input

5
1 3 4 3 3

Output

4 2 1 1 1 

Input

5
1 3 4 3 3

Output

8 4 3 2 1 1 1 1 

Note

For the first sample testcase, some optimal ways of dividing army into squads for each k are:

1. [1], [3], [4], [3, 3]
2. [1], [3, 4, 3, 3]
3. [1, 3, 4, 3, 3]
4. [1, 3, 4, 3, 3]
5. [1, 3, 4, 3, 3]

For the second testcase, some optimal ways of dividing army into squads for each k are:

1. [1], [5], [7], [8], [1], [7], [6], [1]
2. [1, 5], [7, 8], [1, 7], [6, 1]
3. [1, 5, 7], [8], [1, 7, 6, 1]
4. [1, 5, 7, 8], [1, 7, 6, 1]
5. [1, 5, 7, 8, 1, 7, 6, 1]
6. [1, 5, 7, 8, 1, 7, 6, 1]
7. [1, 5, 7, 8, 1, 7, 6, 1]
8. [1, 5, 7, 8, 1, 7, 6, 1]

题解

我们用主席树倒着插入，即可维护区间[L,R]的颜色种类数，查询某个k对应的答案时，我们每次找一个尽量长的含有k种颜色的区间，让左端点不停地更新，这样在主席树上查找logn,对于所有k为k+k/2+k/3+...+1为调和级数nlnn，可以通过

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int sum[N * 40], L[N * 40], R[N * 40], T[N];
int cnt;
int build(int l, int r) {
    int rt = ++cnt;
    int mid = (l + r) >> 1;
    sum[rt] = 0;
    if (l < r) {
        L[rt] = build(l, mid);
        R[rt] = build(mid + 1, r);
    }
    return rt;
}
int update(int pre, int l, int r, int x, int v) {
    int rt = ++cnt;
    L[rt] = L[pre], R[rt] = R[pre], sum[rt] = sum[pre] + v;
    int mid = (l + r) >> 1;
    if (l < r) {
        if (x <= mid) L[rt] = update(L[pre], l, mid, x, v);
        else R[rt] = update(R[pre], mid + 1, r, x, v);
    }
    return rt;
}
int query(int u, int l, int r, int k) {
    if (k < 0) return -1;
    if (l >= r) {
        if (sum[u] <= k) return l;
        else return -1;
    }
    int mid = (l + r) >> 1;
    int x = sum[L[u]];
    if (k == x) {
        return max(query(L[u], l, mid, k), query(R[u], mid + 1, r, 0));
    }
    else if (k < x) return query(L[u], l, mid, k);
    else return query(R[u], mid + 1, r, k - x);
}
int pos[N];
int main() {
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
    }
    T[n + 1] = build(1, n);
    for (int i = n; i >= 1; i--) {
        if (!pos[a[i]]) {
            T[i] = update(T[i + 1], 1, n, i, 1);
            pos[a[i]] = i;
        }
        else {
            T[i] = update(T[i + 1], 1, n, i, 1);
            T[i] = update(T[i], 1, n, pos[a[i]], -1);
            pos[a[i]] = i;
        }
    }
    for (int k = 1; k <= n; k++) {
        int l = 1;
        int res = 0;
        while (l <= n) {
            l = query(T[l], 1, n, k) + 1; res++;
        }
        printf("%d ", res);
    }
    return 0;
}