简介
线段树是一种二叉搜索树,它从上至下逐步将一个大区间划分成一些更小的单元区间,每个区间对应线段树中的一个节点
树中的每个节点代表着一段区间[L,R],每个节点(除叶子节点)的左儿子代表的区间为[L,mid],右儿子则为[mid+1,r]。可以发现对于一个节点来说,左右儿子所代表的区间加起来正好为当前节点的区间
叶子节点的所代表的长度为1,根节点代表的区间为整个序列区间
性质
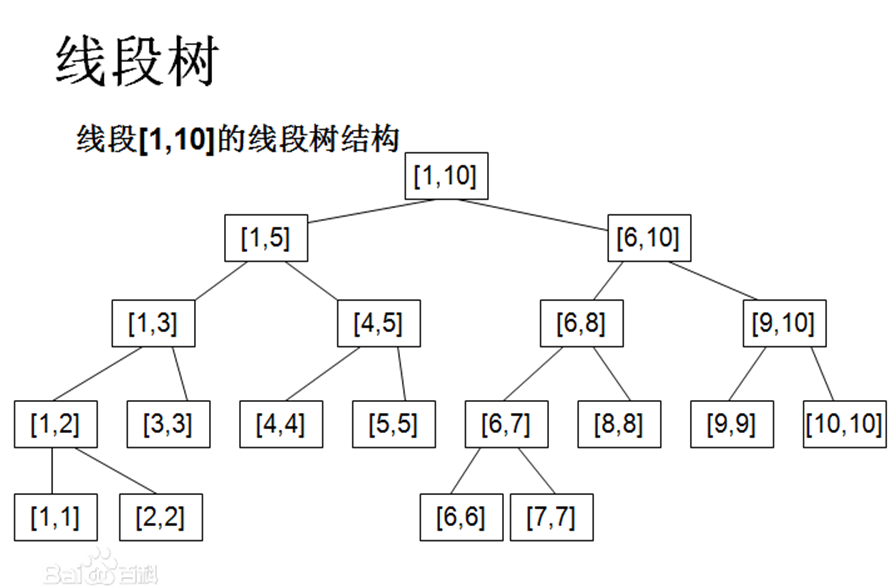
从图中我们可以看到,从根出发,到任意一个节点的距离为logn
对于任意一个区间[L,R],我们可以把它划分为logn个存在于线段树中的区间
对于此线段树维护的序列中的每个元素来说,他都被包含在logn个存在于线段树的区间中,而且这些区间构成一条从根到叶子的路径,同时这个叶子必然代表的是这个元素本身
应用
解决区间问题,如多次询问区间和,多次询问区间最大(小)值等,其中也有所不同,分为区间修改,点修改,区间询问,点询问
下面看一些题目
HDU-1754 I Hate It
题目链接
https://vjudge.net/problem/HDU-1754
题面
Description
很多学校流行一种比较的习惯。老师们很喜欢询问,从某某到某某当中,分数最高的是多少。
这让很多学生很反感。
不管你喜不喜欢,现在需要你做的是,就是按照老师的要求,写一个程序,模拟老师的询问。当然,老师有时候需要更新某位同学的成绩。
Input
本题目包含多组测试,请处理到文件结束。
在每个测试的第一行,有两个正整数 N 和 M ( 0<N<=200000,0<M<5000 ),分别代表学生的数目和操作的数目。
学生ID编号分别从1编到N。
第二行包含N个整数,代表这N个学生的初始成绩,其中第i个数代表ID为i的学生的成绩。
接下来有M行。每一行有一个字符 C (只取'Q'或'U') ,和两个正整数A,B。
当C为'Q'的时候,表示这是一条询问操作,它询问ID从A到B(包括A,B)的学生当中,成绩最高的是多少。
当C为'U'的时候,表示这是一条更新操作,要求把ID为A的学生的成绩更改为B。
Output
对于每一次询问操作,在一行里面输出最高成绩。
Sample Input
5 6
1 2 3 4 5
Q 1 5
U 3 6
Q 3 4
Q 4 5
U 2 9
Q 1 5
Sample Output
5
6
5
9
题解
典型的单点修改,区间询问最大值,用线段树维护即可,注意询问最大值时,query函数与区间和query函数的不同
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#define lson (o << 1)
#define rson (o << 1 | 1)
#define N 200005
using namespace std;
int a[N];
int maxv[N << 2];
int n, m;
int max(int a, int b) {
return a > b ? a : b;
}
void pushup(int o) {
maxv[o] = max(maxv[lson], maxv[rson]);
}
void build(int o, int l, int r) {
if (l == r) {
maxv[o] = a[l];
return;
}
int mid = (l + r) >> 1;
build(lson, l, mid); build(rson, mid + 1, r);
pushup(o);
}
void update(int o, int l, int r, int pos, int v) {
if (l == r) {
maxv[o] = v;
return;
}
if (l > r) return;
int mid = (l + r) >> 1;
if (pos <= mid)
update(lson, l, mid, pos, v);
else update(rson, mid + 1, r, pos, v);
pushup(o);
}
int query(int o, int l, int r, int ql, int qr) {
if (l == ql && r == qr) {
return maxv[o];
}
if (l > r) return 0;
int mid = (l + r) >> 1;
if (qr <= mid) return query(lson, l, mid, ql, qr);
else if (ql > mid) return query(rson, mid + 1, r, ql, qr);
else return max(query(lson, l, mid, ql, mid), query(rson, mid + 1, r, mid + 1, qr));
}
int main() {
while (scanf("%d%d", &n, &m) != EOF) {
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
memset(maxv, 0, sizeof(maxv));
build(1, 1, n);
for (int i = 1; i <= m; i++) {
char ch[2];
scanf("%s", ch);
if (ch[0] == 'Q') {
int l, r;
scanf("%d%d", &l, &r);
printf("%d
", query(1, 1, n, l, r));
}
else {
int pos, v;
scanf("%d%d", &pos, &v);
update(1, 1, n, pos, v);
}
}
}
return 0;
}
POJ-3468 A Simple Problem with Integers
题目链接
https://vjudge.net/problem/POJ-3468
题面
Description
You have N integers, A1, A2, ... , AN. You need to deal with two kinds of operations. One type of operation is to add some given number to each number in a given interval. The other is to ask for the sum of numbers in a given interval.
Input
The first line contains two numbers N and Q. 1 ≤ N,Q ≤ 100000.
The second line contains N numbers, the initial values of A1, A2, ... , AN. -1000000000 ≤ Ai ≤ 1000000000.
Each of the next Q lines represents an operation.
"C a b c" means adding c to each of Aa, Aa+1, ... , Ab. -10000 ≤ c ≤ 10000.
"Q a b" means querying the sum of Aa, Aa+1, ... , Ab.
Output
You need to answer all Q commands in order. One answer in a line.
Sample Input
10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4
Sample Output
4
55
9
15
Hint
The sums may exceed the range of 32-bit integers.
题解
典型的区间修改区间求和,需要用到懒标记和pushdown函数下传懒标记。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#define lson (o << 1)
#define rson (o << 1 | 1)
#define N 200005
using namespace std;
typedef long long ll;
ll a[N];
ll sumv[N << 2];
ll addv[N << 2];
int n, m;
void pushup(int o) {
sumv[o] = sumv[lson] + sumv[rson];
}
void pushdown(int o, int l, int r) {
if (addv[o]) {
addv[lson] += addv[o];
addv[rson] += addv[o];
ll mid = (l + r) >> 1;
sumv[lson] += (ll)(mid - l + 1) * addv[o];
sumv[rson] += (ll)(r - mid) * addv[o];
addv[o] = 0;
}
}
void build(int o, int l, int r) {
addv[o] = 0;
if (l == r) {
sumv[o] = a[l];
return;
}
int mid = (l + r) >> 1;
build(lson, l, mid); build(rson, mid + 1, r);
pushup(o);
}
void update(int o, int l, int r, int ql, int qr, int v) {
if (ql <= l && r <= qr) {
sumv[o] += (ll)(r - l + 1) * v;
addv[o] += v;
return;
}
int mid = (l + r) >> 1;
pushdown(o, l, r);
if (ql <= mid) update(lson, l, mid, ql, qr, v);
if (qr > mid) update(rson, mid + 1, r, ql, qr, v);
pushup(o);
}
ll query(int o, int l, int r, int ql, int qr) {
if (ql <= l && r <= qr) {
return sumv[o];
}
int mid = (l + r) >> 1;
ll ans = 0;
pushdown(o, l, r);
if (ql <= mid) ans += query(lson, l, mid, ql, qr);
if (qr > mid) ans += query(rson, mid + 1, r, ql, qr);
return ans;
}
int main() {
while (scanf("%d%d", &n, &m) != EOF) {
for (int i = 1; i <= n; i++) {
scanf("%lld", &a[i]);
}
memset(sumv, 0, sizeof(sumv));
memset(addv, 0, sizeof(addv));
build(1, 1, n);
for (int i = 1; i <= m; i++) {
char ch[2];
scanf("%s", ch);
if (ch[0] == 'Q') {
int l, r;
scanf("%d%d", &l, &r);
printf("%lld
", query(1, 1, n, l, r));
}
else {
int l, r, v;
scanf("%d%d%d", &l, &r, &v);
update(1, 1, n, l, r, v);
}
}
}
return 0;
}
HDU-1166 敌兵布阵
题目链接
https://vjudge.net/problem/HDU-1166
此题较水,没什么贴题面的价值
题解
只需要将上面的区间修改的ql=qr=要修改的点即可,代码不贴了,和上个题是重题
HDU-3577 Fast Arrangement(有点坑)
题目链接
https://vjudge.net/problem/13570/origin
题面
Description
Chinese always have the railway tickets problem because of its' huge amount of passangers and stations. Now goverment need you to develop a new tickets query system.
One train can just take k passangers. And each passanger can just buy one ticket from station a to station b. Each train cannot take more passangers any time. The one who buy the ticket earlier which can be sold will always get the ticket.
Input
The input contains servel test cases. The first line is the case number. In each test case:
The first line contains just one number k( 1 ≤ k ≤ 1000 ) and Q( 1 ≤ Q ≤ 100000 )
The following lines, each line contains two integers a and b, ( 1 ≤ a < b ≤ 1000000 ), indicate a query.
Huge Input, scanf recommanded.
Output
For each test case, output three lines:
Output the case number in the first line.
If the ith query can be satisfied, output i. i starting from 1. output an blank-space after each number.
Output a blank line after each test case.
Sample Input
1
3 6
1 6
1 6
3 4
1 5
1 2
2 4
Sample Output
Case 1:
1 2 3 5
题解
这题不用离散化也可以过,典型的区间修改,区间询问最大值,注意有一个坑点,那就是对于第i次区间,乘客在a[i]上车,在b[i]下车,所以乘车区间是([a[i], b[i]-1])
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define lson (o << 1)
#define rson (o << 1 | 1)
#define N 1000005
using namespace std;
typedef long long ll;
int a[N], b[N];
int lis[N];
ll maxv[N << 2];
ll addv[N << 2];
int k, q;
int max(int a, int b) {
return a > b ? a : b;
}
void pushup(int o) {
maxv[o] = max(maxv[lson], maxv[rson]);
}
void pushdown(int o, int l, int r) {
if (addv[o]) {
addv[lson] += addv[o];
addv[rson] += addv[o];
maxv[lson] += addv[o];
maxv[rson] += addv[o];
addv[o] = 0;
}
}
void build(int o, int l, int r) {
addv[o] = 0;
if (l == r) {
maxv[o] = 0;
return;
}
int mid = (l + r) >> 1;
build(lson, l, mid); build(rson, mid + 1, r);
pushup(o);
}
void update(int o, int l, int r, int ql, int qr, int v) {
if (ql <= l && r <= qr) {
maxv[o] += v;
addv[o] += v;
return;
}
int mid = (l + r) >> 1;
pushdown(o, l, r);
if (ql <= mid) update(lson, l, mid, ql, qr, v);
if (qr > mid) update(rson, mid + 1, r, ql, qr, v);
pushup(o);
}
ll query(int o, int l, int r, int ql, int qr) {
if (ql == l && r == qr) {
return maxv[o];
}
int mid = (l + r) >> 1;
pushdown(o, l, r);
if (qr <= mid) return query(lson, l, mid, ql, qr);
else if (ql > mid) return query(rson, mid + 1, r, ql, qr);
else return max(query(lson, l, mid, ql, mid), query(rson, mid + 1, r, mid + 1, qr));
}
int main() {
int t;
scanf("%d", &t);
int cnt = 0;
while (t--) {
cnt++;
scanf("%d%d", &k, &q);
memset(maxv, 0, sizeof(maxv));
memset(addv, 0, sizeof(addv));
printf("Case %d:
", cnt);
int cnt1 = 0;
for (int i = 1; i <= q; i++) {
scanf("%d%d", &a[i], &b[i]);
b[i]--;
}
build(1, 1, 1000000);
for (int i = 1; i <= q; i++) {
int tmp = query(1, 1, 1000000, a[i], b[i]);
if (tmp <= k - 1) {
printf("%d ", i);
update(1, 1, 1000000, a[i], b[i], 1);
}
else continue;
}
printf("
");
printf("
");
}
return 0;
}
HDU-1698 Just a Hook
题目链接
https://vjudge.net/problem/15763/origin
题面
Description
In the game of DotA, Pudge’s meat hook is actually the most horrible thing for most of the heroes. The hook is made up of several consecutive metallic sticks which are of the same length.
Now Pudge wants to do some operations on the hook.
Let us number the consecutive metallic sticks of the hook from 1 to N. For each operation, Pudge can change the consecutive metallic sticks, numbered from X to Y, into cupreous sticks, silver sticks or golden sticks.
The total value of the hook is calculated as the sum of values of N metallic sticks. More precisely, the value for each kind of stick is calculated as follows:
For each cupreous stick, the value is 1.
For each silver stick, the value is 2.
For each golden stick, the value is 3.
Pudge wants to know the total value of the hook after performing the operations.
You may consider the original hook is made up of cupreous sticks.
Input
The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 10 cases.
For each case, the first line contains an integer N, 1<=N<=100,000, which is the number of the sticks of Pudge’s meat hook and the second line contains an integer Q, 0<=Q<=100,000, which is the number of the operations.
Next Q lines, each line contains three integers X, Y, 1<=X<=Y<=N, Z, 1<=Z<=3, which defines an operation: change the sticks numbered from X to Y into the metal kind Z, where Z=1 represents the cupreous kind, Z=2 represents the silver kind and Z=3 represents the golden kind.
Output
For each case, print a number in a line representing the total value of the hook after the operations. Use the format in the example.
Sample Input
1
10
2
1 5 2
5 9 3
Sample Output
Case 1: The total value of the hook is 24.
题解
简单说下题意,题中给定一个n,一开始是n个价值为1的cupreous stick,后面有q次修改,每次让区间([l,r])内的stick变换种类,问最后所有棍子的总价值
直接线段树维护,一开始所有节点价值为1,后面修改直接将区间内的点都变成相应种类的棍即可,莫名奇妙wa了两发,大概是集训过后没写题的后遗症
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define lson (o << 1)
#define rson (o << 1 | 1)
#define N 100005
using namespace std;
typedef long long ll;
ll sumv[N << 2];
ll addv[N << 2];
int n, q;
int max(int a, int b) {
return a > b ? a : b;
}
void pushup(int o) {
sumv[o] = sumv[lson] + sumv[rson];
}
void pushdown(int o, int l, int r) {
if (addv[o]) {
addv[rson] = addv[o];
addv[lson] = addv[o];
int mid = (l + r) >> 1;
sumv[lson] = addv[o] * (mid - l + 1);
sumv[rson] = addv[o] * (r - mid);
addv[o] = 0;//别忘清标记
}
}
void build(int o, int l, int r) {
if (l == r) {
sumv[o] = 1;
return;
}
int mid = (l + r) >> 1;
build(lson, l, mid); build(rson, mid + 1, r);
pushup(o);
}
void update(int o, int l, int r, int ql, int qr, int v) {
if (ql <= l && r <= qr) {
sumv[o] = v * (r - l + 1);
addv[o] = v;
return;
}
int mid = (l + r) >> 1;
pushdown(o, l, r);
if (ql <= mid) update(lson, l, mid, ql, qr, v);
if (qr > mid) update(rson, mid + 1, r, ql, qr, v);
pushup(o);
}
int main() {
int t;
scanf("%d", &t);
int cnt = 0;
while (t--) {
cnt++;
scanf("%d", &n);
scanf("%d", &q);
memset(sumv, 0, sizeof(sumv));
memset(addv, 0, sizeof(addv));
printf("Case %d: The total value of the hook is ", cnt);
build(1, 1, n);
for (int i = 1; i <= q; i++) {
int l, r, k;
scanf("%d%d%d", &l, &r, &k);
update(1, 1, n, l, r, k);
}
printf("%d.
", sumv[1]);
}
return 0;
}
POJ-2528 Mayor's posters(有点难度)
题目链接
https://vjudge.net/problem/14608/origin
题面
Description
The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules:
- Every candidate can place exactly one poster on the wall.
- All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown).
- The wall is divided into segments and the width of each segment is one byte.
- Each poster must completely cover a contiguous number of wall segments.
They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections.
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall.
Input
The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers l i and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= l i <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered l i, l i+1 ,... , ri.
Output
For each input data set print the number of visible posters after all the posters are placed.
The picture below illustrates the case of the sample input.

Sample Input
1
5
1 4
2 6
8 10
3 4
7 10
Sample Output
4
题解
vj上没有现在的这张图,然后我读错题做了假题,题意是给定n张海报,每张海报会相互覆盖,后面加入的会覆盖前面已有的海报(我就是以为是前面如果一个位置已经有了海报,后面的海报如果有重叠,那么重叠部分属于前面的海报)。问最后能看到多少张海报。
其实发现自己读错题之后,发现只要倒着处理就可以完全按照我原来的做法了(先贴的海报不会被覆盖,后贴的海报在下面)这样就可以维护一个区间最小值,如果要贴海报的位置有等于零的部分,那么证明它可以被看到,线段树维护即可
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define lson (o << 1)
#define rson (o << 1 | 1)
#define N 10050
using namespace std;
typedef long long ll;
int L[N], R[N];
int lis[N * 2];
int minv[N << 3];
int addv[N << 3];
int min(int a, int b) {
return a < b ? a : b;
}
int pushup(int o) {
minv[o] = min(minv[lson], minv[rson]);
}
int pushdown(int o, int l, int r) {
if (addv[o]) {
addv[lson] += addv[o];
addv[rson] += addv[o];
minv[lson] += addv[o];
minv[rson] += addv[o];
addv[o] = 0;
}
}
void build(int o, int l, int r) {
if (l == r) {
minv[o] = 0;
return;
}
int mid = (l + r) >> 1;
build(lson, l, mid); build(rson, mid + 1, r);
pushup(o);
}
void update(int o, int l, int r, int ql, int qr) {
if (ql <= l && r <= qr) {
minv[o] += 1;
addv[o] += 1;
return;
}
int mid = (l + r) >> 1;
pushdown(o, l, r);
if (ql <= mid) update(lson, l, mid, ql, qr);
if (qr > mid) update(rson, mid + 1, r, ql, qr);
pushup(o);
}
int query(int o, int l, int r, int ql, int qr) {
if (ql == l && r == qr) {
return minv[o];
}
int mid = (l + r) >> 1;
pushdown(o, l, r);
if (qr <= mid) return query(lson, l, mid, ql, qr);
else if (ql > mid) return query(rson, mid + 1, r, ql, qr);
else return min(query(lson, l, mid, ql, mid), query(rson, mid + 1, r, mid + 1, qr));
}
int main() {
int t;
scanf("%d", &t);
while (t--) {
int m;
scanf("%d", &m);
memset(minv, 0, sizeof(minv));
memset(addv, 0, sizeof(addv));
for (int i = 1; i <= m; i++) {
scanf("%d%d", &L[i], &R[i]);
lis[2 * i - 1] = L[i]; lis[2 * i] = R[i];
}
sort(lis + 1, lis + 2 * m + 1);
int last = unique(lis + 1, lis + 2 * m + 1) - lis - 1;
for (int i = 1; i <= m; i++) {
L[i] = lower_bound(lis + 1, lis + last + 1, L[i]) - lis;
R[i] = lower_bound(lis + 1, lis + last + 1, R[i]) - lis;
}
int n = last;
int ans = 0;
for (int i = m; i >= 1; i--) {
if (query(1, 1, n, L[i], R[i]) == 0) {
ans++;
update(1, 1, n, L[i], R[i]);
}
}
printf("%d
", ans);
}
}
CodeForces-1000F One Occurrence(难)
题目链接
https://vjudge.net/problem/1645217/origin
题面
Description
You are given an array (a) consisting of (n) integers, and (q) queries to it. (i)-th query is denoted by two integers (l_i) and (r_i). For each query, you have to find any integer that occurs exactly once in the subarray of (a) from index (l_i) to index (r_i) (a subarray is a contiguous subsegment of an array). For example, if (a = [1, 1, 2, 3, 2, 4]), then for query ((l_i = 2, r_i = 6)) the subarray we are interested in is ([1, 2, 3, 2, 4]), and possible answers are (1), (3) and (4); for query ((l_i = 1, r_i = 2)) the subarray we are interested in is ([1, 1]), and there is no such element that occurs exactly once.
Can you answer all of the queries?
Input
The first line contains one integer (n) ((1 le n le 5 cdot 10^5)).
The second line contains (n) integers (a_1, a_2, dots, a_n) ((1 le a_i le 5 cdot 10^5)).
The third line contains one integer (q) ((1 le q le 5 cdot 10^5)).
Then (q) lines follow, (i)-th line containing two integers (l_i) and (r_i) representing (i)-th query ((1 le l_i le r_i le n)).
Output
Answer the queries as follows:
If there is no integer such that it occurs in the subarray from index (l_i) to index (r_i) exactly once, print (0). Otherwise print any such integer.
Example
Input
6
1 1 2 3 2 4
2
2 6
1 2
Output
4
0
题意
给定n个数字,q次询问,每次询问([l,r])内只出现一次的数字,如果有的话随便输出一个,没有的话输出0
题解
首先我们我们可以从小到大推出从1到now中,所有数字上一次出现最近在哪。假设我们用pos[a[i]]表示a[i]最近一次出现在哪,那么对于样例来说,从1到n循环,到1时,更新pos[1] = 1, 到2时,更新pos[1] = 2; 到3时,更新pos[2] = 3; pos[1] = 2;....到5时,更新pos[2] = 5....
然后对于询问([l,r])内有没有出现过一次的数,我们可以用一个线段树维护([l,r])中出现的数上一次出现最近在哪的最小值,这样(query(1, 1,n,Q[i].l,Q[i].r))就可得到上一次出现的最小位置,看看这个位置是否小于(Q[i].l)即可。
又由于pos的更新是递推实现的,对于([l,r])的询问,如果更新的pos大于r那么就会得到错误的答案,所以可以想到先把询问存下来,按右端点排序,在递推过程中推到(i)时判断一下当前询问右端点和(i)是否相等,相等就计算这次询问即可
还要注意更新pos[i]时要消除上一次pos[i]的影响,由于我们是求最小值,将它在线段树中的值设为inf即可
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define lson (o << 1)
#define rson (o << 1 | 1)
#define N 500050
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;
int a[N];
int ans[N];
int pos[N];
struct node {
int l, r, id;
} Q[N];
struct tree {
int pos, pre;
tree(int pos = 0, int pre = 0): pos(pos), pre(pre) {}
bool operator < (const tree &b) const {
return pre < b.pre;
}
} minv[N << 2];
bool cmp(node a, node b) {
if (a.r == b.r) return a.l < b.l;
else return a.r < b.r;
}
void pushup(int o) {
minv[o] = min(minv[lson], minv[rson]);
}
void update(int o, int l, int r, int pos, int pre) {
if (l == r) {
minv[o] = tree(pos, pre);
return;
}
int mid = (l + r) >> 1;
if (pos <= mid) update(lson, l, mid, pos, pre);
if (pos > mid) update(rson, mid + 1, r, pos, pre);
pushup(o);
}
tree query(int o, int l, int r, int ql, int qr) {
if (ql == l && qr == r) {
return minv[o];
}
int mid = (l + r) >> 1;
if (qr <= mid) return query(lson, l, mid, ql, qr);
else if (ql > mid) return query(rson, mid + 1, r, ql, qr);
else return min(query(lson, l, mid, ql, mid), query(rson, mid + 1, r, mid + 1, qr));
}
int main() {
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
int q;
scanf("%d", &q);
for (int i = 1; i <= q; i++) {
scanf("%d%d", &Q[i].l, &Q[i].r);
Q[i].id = i;
}
sort (Q + 1, Q + q + 1, cmp);
int j = 1;
for (int i = 1; i <= n; i++) {
if (pos[a[i]]) update(1, 1, n, pos[a[i]], inf);
update(1, 1, n, i, pos[a[i]]);
while (Q[j].r == i && j <= q) {
tree now = query(1, 1, n, Q[j].l, Q[j].r);
if (now.pre < Q[j].l) {
ans[Q[j].id] = a[now.pos];
}
j++;
}
pos[a[i]] = i;
}
for (int i = 1; i <= q; i++) {
printf("%d
", ans[i]);
}
return 0;
}
HDU-6315 Naive Operations(稍难)
题目链接
https://vjudge.net/problem/HDU-6315
题面
Description
In a galaxy far, far away, there are two integer sequence a and b of length n.
b is a static permutation of 1 to n. Initially a is filled with zeroes.
There are two kind of operations:
-
add l r: add one for (a_l,a_{l+1}...a_r)
-
query l r: query (sum_{i=l}^r lfloor a_i / b_i floor)
Input
There are multiple test cases, please read till the end of input file.
For each test case, in the first line, two integers n,q, representing the length of a,b and the number of queries.
In the second line, n integers separated by spaces, representing permutation b.
In the following q lines, each line is either in the form 'add l r' or 'query l r', representing an operation.
(1 leq n,q leq 100000), (1 leq l leq r leq n), there're no more than 5 test cases.
Output
Output the answer for each 'query', each one line.
Sample Input
5 12
1 5 2 4 3
add 1 4
query 1 4
add 2 5
query 2 5
add 3 5
query 1 5
add 2 4
query 1 4
add 2 5
query 2 5
add 2 2
query 1 5
Sample Output
1
1
2
4
4
6
题意
给定两个序列(a,b),(a)初始全为0, (b)初始为n的一个排列,有两种操作,一是对a进行区间加,二是询问(sum_{i=l}^r lfloor a_i / b_i floor)的值
题解
用线段树维护两个值,一是区间最小值,初始为b序列,每次区间加让对应的b序列区间减,减到零时更新第二个维护的值,也就是要询问的(sum_{i=l}^r lfloor a_i / b_i floor),因为如果b序列对应的某个区间最小值为0,说明有一个点i,值刚好(a[i]=b[i]),此时这点答案+1,区间更新。
如何维护,同样适用懒标记,在区间最小值不为0时,直接更新懒标记,在区间最小值为0时,递归找到变成零的某一点,将它重新变成(b[i]),然后这个点的(sum+1),一路更新即可,询问就与普通的区间和一样了。
代码
#include <cstdio>
#include <cstring>
#define lson (o << 1)
#define rson (o << 1 | 1)
#define N 100005
using namespace std;
int sumv[N << 2];
int minv[N << 2];
int lazy[N << 2];
int b[N];
int min(int a, int b) {
return a < b ? a : b;
}
void pushup(int o) {
sumv[o] = sumv[lson] + sumv[rson];
minv[o] = min(minv[lson], minv[rson]);
}
void pushdown(int o) {
if (lazy[o]) {
lazy[lson] += lazy[o];
lazy[rson] += lazy[o];
minv[lson] -= lazy[o];
minv[rson] -= lazy[o];
lazy[o] = 0;
}
}
void build(int o, int l, int r) {
if (l == r) {
minv[o] = b[l];
return;
}
int mid = (l + r) >> 1;
build(lson, l, mid); build(rson, mid + 1, r);
pushup(o);
}
void update(int o, int l, int r, int ql, int qr) {
if (ql <= l && r <= qr) {
minv[o]--;
if (minv[o] > 0) {
lazy[o]++;
return;
}
else {
if (l == r) {
sumv[o]++;
minv[o] = b[l];
return;
}
}
}
int mid = (l + r) >> 1;
pushdown(o);
if (ql <= mid) update(lson, l, mid, ql, qr);
if (qr > mid) update(rson, mid + 1, r, ql, qr);
pushup(o);
}
int query(int o, int l, int r, int ql, int qr) {
if (ql <= l && r <= qr) {
return sumv[o];
}
pushdown(o);
int mid = (l + r) >> 1;
int sum = 0;
if (ql <= mid) sum += query(lson, l, mid, ql, qr);
if (qr > mid) sum += query(rson, mid + 1, r, ql, qr);
return sum;
}
int main() {
int n, m;
while (scanf("%d%d", &n, &m) != EOF) {
memset(sumv, 0, sizeof(sumv));
memset(minv, 0, sizeof(minv));
memset(lazy, 0, sizeof(lazy));
for (int i = 1; i <= n; i++) {
scanf("%d", &b[i]);
}
build(1, 1, n);
char ch[10];
for (int i = 1; i <= m; i++) {
scanf("%s", ch);
int l, r;
if (ch[0] == 'a') {
scanf("%d%d", &l, &r);
update(1, 1, n, l, r);
}
else {
scanf("%d%d", &l, &r);
printf("%d
", query(1, 1, n, l, r));
}
}
}
return 0;
}
还有几题,待补