题目链接
https://vjudge.net/problem/UVA-12627
题面
Description
Piotr found a magical box in heaven. Its magic power is that if you place any red balloon inside it
then, after one hour, it will multiply to form 3 red and 1 blue colored balloons. Then in the next hour,
each of the red balloons will multiply in the same fashion, but the blue one will multiply to form 4 blue
balloons. This trend will continue indefinitely.
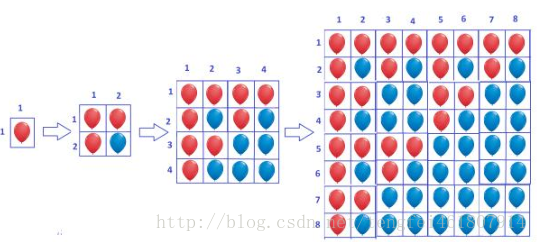
The arrangements of the balloons after the 0-th, 1-st, 2-nd and 3-rd hour are depicted in the
following diagram.
As you can see, a red balloon in the cell (i, j) (that is i-th row and j-th column) will multiply to
produce 3 red balloons in the cells (i ∗ 2 − 1, j ∗ 2 − 1), (i ∗ 2 − 1, j ∗ 2), (i ∗ 2, j ∗ 2 − 1) and a blue
balloon in the cell (i ∗ 2, j ∗ 2). Whereas, a blue balloon in the cell (i, j) will multiply to produce 4 blue
balloons in the cells (i ∗ 2 − 1, j ∗ 2 − 1), (i ∗ 2 − 1, j ∗ 2), (i ∗ 2, j ∗ 2 − 1) and (i ∗ 2, j ∗ 2). The grid size
doubles (in both the direction) after every hour in order to accommodate the extra balloons.
In this problem, Piotr is only interested in the count of the red balloons; more specifically, he would
like to know the total number of red balloons in all the rows from A to B after K-th hour.
Input
The first line of input is an integer T (T < 1000) that indicates the number of test cases. Each case
contains 3 integers K, A and B. The meanings of these variables are mentioned above. K will be in
the range [0, 30] and 1 ≤ A ≤ B ≤ 2
K.
Output
For each case, output the case number followed by the total number of red balloons in rows [A, B] after
K-th hour.
Sample Input
3
0 1 1
3 1 8
3 3 7
Sample Output
Case 1: 1
Case 2: 27
Case 3: 14
题意
按题中所给方式进行扩展,问第k次扩展后([A,B])中的红气球数量
题解
直接递归处理,首先对于每一次扩展后的气球,很容易发现气球数量为(3^k),先将这个预处理出来,然后递归处理,
计算从第一列到第B行的红气球数减去第一列到第A-1列的红气球数即为答案,如果要计算的列数大于一半,左半边就可以直接使用预处理出的答案,右边递归处理,不大于一半直接递归即可。
AC代码
#include <iostream>
#include <cstdio>
#include <cstring>
#define N 50
using namespace std;
long long f[N];
int fpow(int a, int b) {
int ans = 1;
while (b) {
if (b & 1) ans *= a;
a *= a;
b >>= 1;
}
return ans;
}
long long dfs(int k,int i){
if(i == 0)
return 0;
if(k == 0)
return 1;
if(i <= fpow(2, k - 1))
return 2 * dfs(k - 1, i);
else
return 2 * f[k - 1] + dfs(k - 1, i - fpow(2, k - 1));
}
int main() {
f[0] = 1;
for (int i = 1; i <= 30; i++) {
f[i] = 3 * f[i - 1];
}
int t;
scanf("%d", &t);
int cnt = 0;
while (t--) {
int k, a, b;
cnt++;
scanf("%d%d%d", &k, &a, &b);
printf("Case %d: %lld
", cnt, dfs(k, b) - dfs(k, a - 1));
}
return 0;
}