递推&&矩阵加速

这个题其实很简单，简单分析一下规律，发现发f[i]=f[i-1]+f[i-2]。

如下图：

 

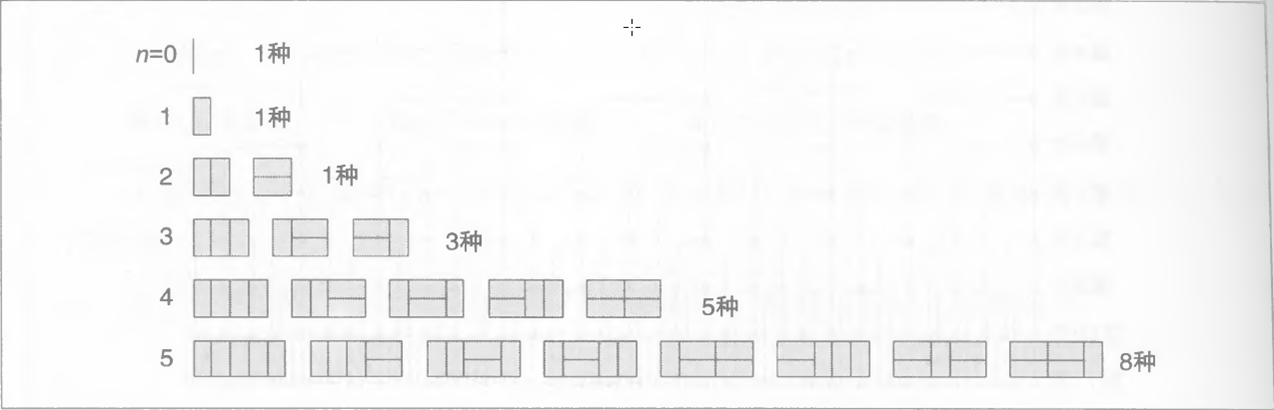
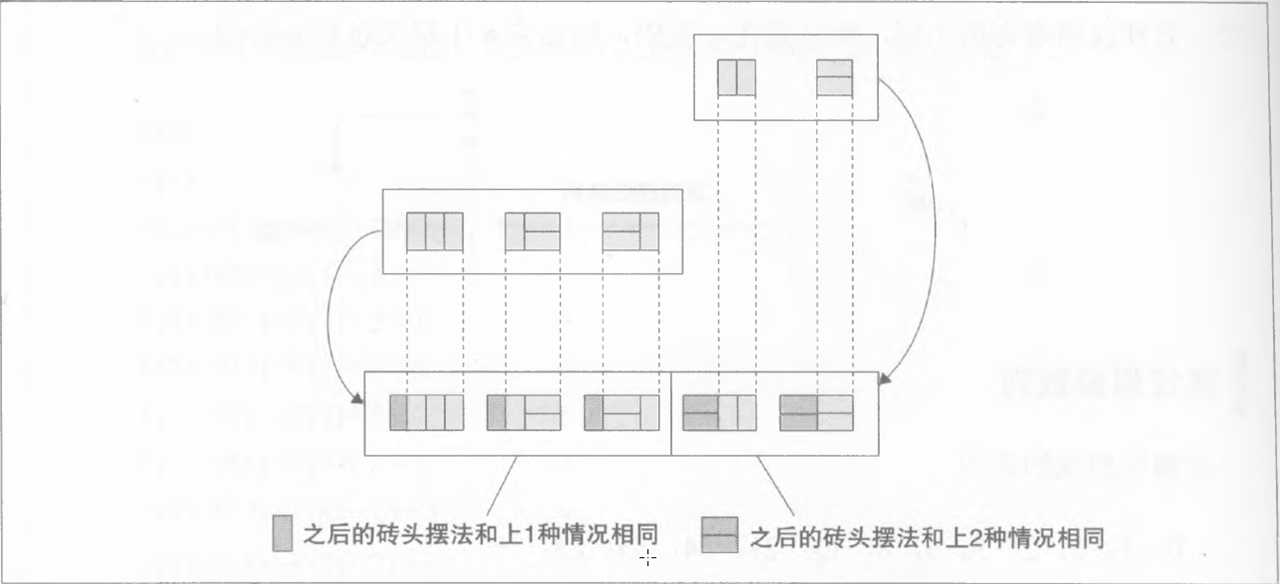
 程序：

#include<iostream>
using namespace std;
int main()
{
  int n,i,j,a[101];                  
  cin>>n;
  a[1]=1;a[2]=2;
  for (i=3;i<=n;i++) 
   {
     a[i]=a[i-1]+a[i-2];
　   }
cout<<a[n];
} 

用这个代码，解决这个题的确很轻松。

可是只要稍微更改一下数据范围，就完全不一样了：

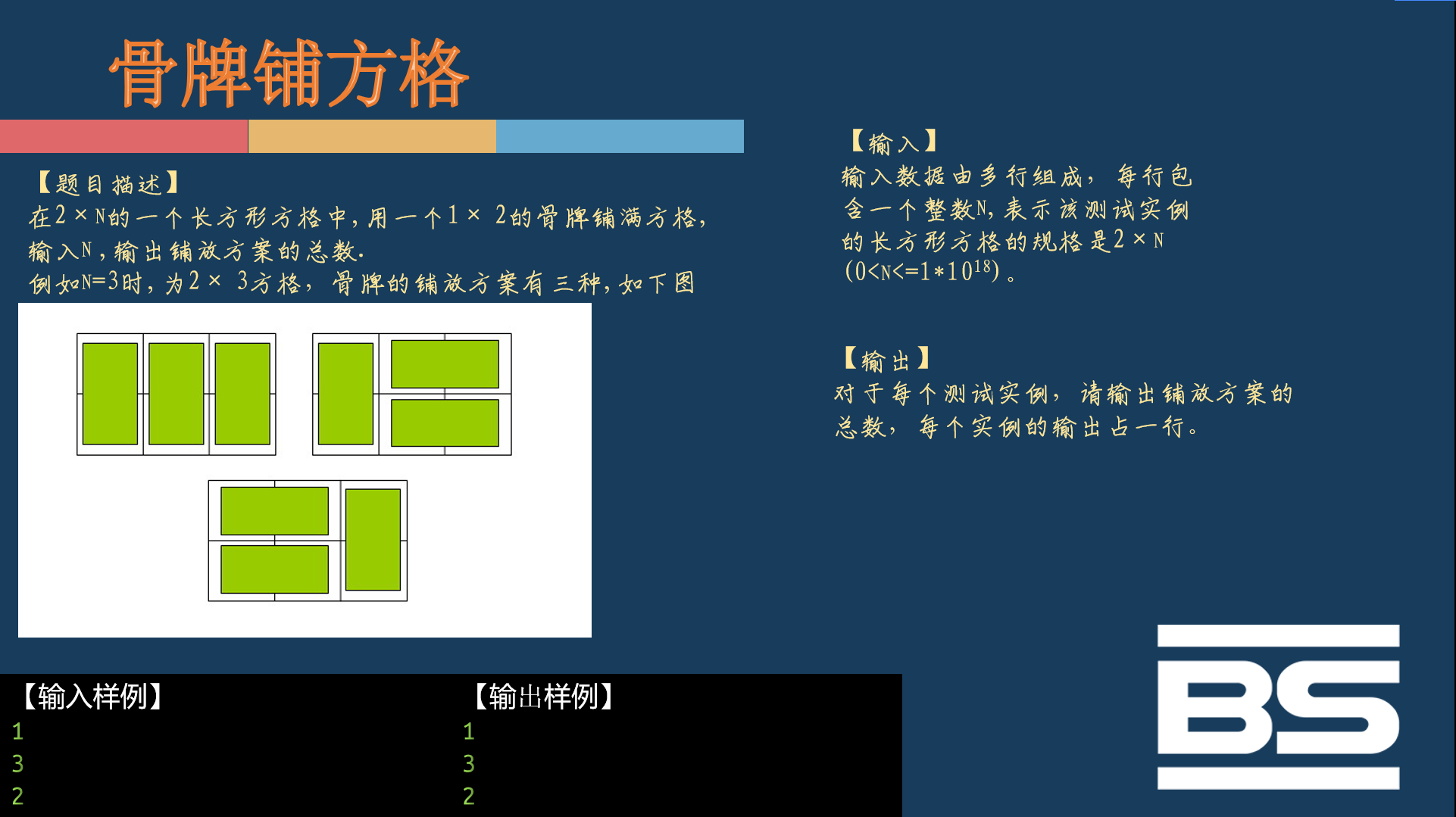
这样子，难度就完全不是一个等级了。

首先是不能开一个1000000000000000000的数组，那样肯定会爆内存。

我们可以用滚动的数组：

 1 #include<bits/stdc++.h>
 2 #define mod 1e9+7
 3 
 4 using namespace std;
 5 
 6 long long a[4] = {0,1,2};
 7 
 8 int main()
 9 {
10     freopen("brick.in", "r", stdin);
11     freopen("brick.out", "w", stdout);
12     int fbk;
13     cin >> fbk;
14     if (fbk==1)
15     {
16         cout << 1;
17     }
18     else if (fbk==2)
19     {
20         cout << 2;
21     }
22     else
23     {
24         for (int yousa = 3; yousa <= fbk-2; yousa++)
25         {
26             a[3] = (a[2] + a[1])%(long long)(mod);
27             a[1] = a[2];
28             a[2] = a[3];
29         }
30         cout << a[3] << "
";
31     }
32     
33     fclose(stdin);
34     fclose(stdout);
35 }

测试之后发现虽然内存占用很少，但是会超时。

这就用到我们的矩阵加速了：

矩阵乘法

矩阵乘法可以先稍作了解，知道矩阵相乘的运算法则

C[i][j]=∑k=1k=5A[i][k]∗B[k][j]

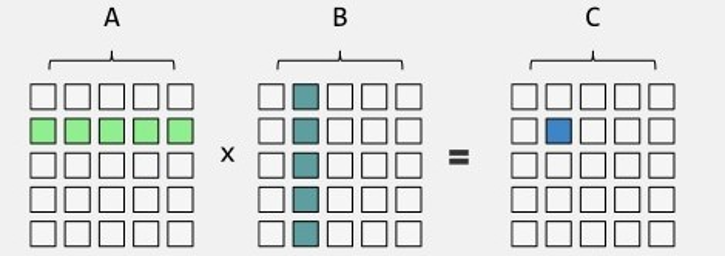
快速幂

快速幂要求解的是这样一类问题：

给你A,B,C，求A的B次方模C的余数

A,C<=10^9,B<=10^18

如果我们线性去求，时间复杂度是O（n）的，但题目中给出的B是很大的数，这样显然会超时,我们可以用快速幂来加速这个过程。

我们可以想像一下小学的时候我们如何计算2^16

2^16=4^8=16^4=256^2=65536

那如何计算2^18呢？

2^18=4^9=4∗4^8=4∗16^4=4∗256^2=4∗65536=262144

快速幂同理也是如此

我们可以按照上面做法，利用分治的思想求去解

这样原本O(n)的时间复杂度便降到了O(log n )

long long ans=1,base=a;
while(n>0){
        if(n&1){
            ans*=base;
        }
        base*=base;
        n=n/2;
    }

矩阵快速幂

矩阵快速幂的原理同快速幂一样，只是转换为了矩阵之间的乘法操作

所以单纯的重载一下运算符(写成函数的形式也可），将普通的乘法转换为矩阵乘法就好了。

矩阵加速

知道那个叫矩阵快速幂的东西后我们可以学矩阵加速了

斐波那契数列中的每一项都是前两项之和

我们考虑构造这么一个矩阵：每一次乘上这个矩阵都能从f[n-1],f[n-2]两项向后递推到f[n-1],f[n]这两项

那么关键就是如何构造这样的矩阵

(1  1

1   0)

对于这样一个矩阵我们有

(f[n−1]f[n−2])∗(1110)=(f[n]f[n−1])(f[n−1]f[n−2])∗(1110)=(f[n]f[n−1])

所以我们将每一次两项相加转换为了乘以一个转移矩阵

既然是乘法，每次乘以的也是同一个矩阵

我们可以利用矩阵快速幂的思想对于求解斐波那契数列加速

代码实现基本上是一致的，只需要构造一个转移矩阵来进行状态之间的转移即可

struct mat{
    ll m[5][5];
}a,ans;
ll n,b,k; 
mat mul(mat x,mat y,int flag){
    mat c;
    for(int i=1;i<=2;i++)
        for(int j=1;j<=2;j++)
            c.m[i][j]=0;
    for(int i=1;i<=2;i++){
        for(int j=1;j<=2;j++){
            for(int q=1;q<=2;q++){
                    c.m[i][j]=(c.m[i][j]+x.m[i][q]*y.m[q][j])%Mod;
        
            }
        }
    }
    return c;
}
int main(){
    cin >> n;
    a.m[1][1]=1;a.m[1][2]=1;
    a.m[2][1]=1;a.m[2][2]=0;
    b=n-2;
    ans.m[1][1]=1;
    ans.m[1][2]=1;
    while(b){
        if(b&1){
            ans=mul(ans,a,1);
        }
        a=mul(a,a,2);
        b=b/2;
    } 
    if(n==1||n==2)cout<<1;
    else cout<<ans.m[1][1]%Mod;
}

这样这个题就被解决了！