问题描述
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
分析
抛开二维数组的有序性质,直接遍历二维数组找是否含有一个数,算法复杂度为(O(n^2))
bool Find(int target, vector<vector<int> > array) {
for(int i = 0; i < array.size(); i++) {
for(int val :array[i]){
if(val == target) {
return true;
}
}
}
return false;
}
二位数组的每一行都是递增的,可以对每一行进行二分查找,算法复杂度为(O(nlogn))
bool Find(int target, vector<vector<int> > array) {
for(int i = 0; i < array.size(); i++) {
int low = 0, high = array[i].size()-1;
while (low <= high) {
int mid = (low + high) / 2;
if (target == array[i][mid]){
return true;
}
else if (target > array[i][mid]) {
low = mid + 1;
} else {
high = mid - 1;
}
}
}
return false;
}
考虑到二维数组的列也是有序的,选择一个初始点,与target比较
- > target, 则target在该初始点左上
- < target, 则target在该初始点右下
只有左下和右上两个点才能作为起始点,其他点会导致移动的方向不确定(如以v[0][0]为初始点时,当v[0][0] < target,target可能在同一行右边,也可能在下面的某行中)
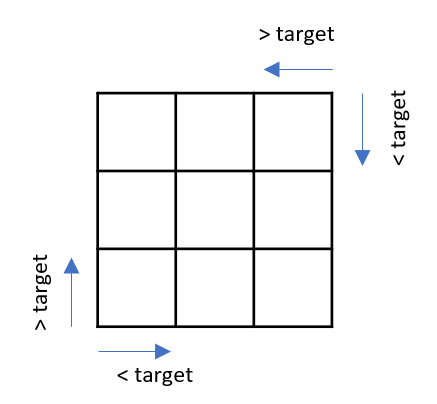
用这种方法,每次可以使问题的规模减少一行或者一列,找到array[p][q]需要p+q+1次
bool Find(int target, vector<vector<int>> array) {
int row = array.size()- 1, col = 0;
while (row >= 0 && col < array[0].size()) {
if (array[row][col] == target)
{
return true;
}
else if (array[row][col] > target) {
--row;
} else {
++col;
}
}
return false;
}