背景:数据挖掘/机器学习中的术语较多,而且我的知识有限。之前一直疑惑正则这个概念。所以写了篇博文梳理下
摘要:
1.正则化(Regularization)
1.1 正则化的目的
1.2 结构风险最小化(SRM)理论
1.3 L1范数(lasso),L2范数(ridge),ElasticNet
1.4为什么说L1是稀疏的,L2是平滑的?
2.归一化 (Normalization)
2.1归一化的目的
2.1归一化计算方法
2.2.spark ml中的归一化
2.3 python中skelearn中的归一化
知识总结:
1.正则化(Regularization)
1.1 正则化的目的:我的理解就是平衡训练误差与模型复杂度的一种方式,通过加入正则项来避免过拟合(over-fitting)。(可以引入拟合时候的龙格现象,然后引入正则化及正则化的选取,待添加)
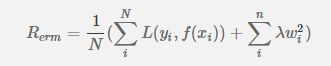
后面的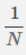
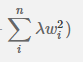 就是正则化项,其中λ越大表明惩罚粒度越大,等于0表示不做惩罚,N表示所有样本的数量,n表示参数的个数。
就是正则化项,其中λ越大表明惩罚粒度越大,等于0表示不做惩罚,N表示所有样本的数量,n表示参数的个数。

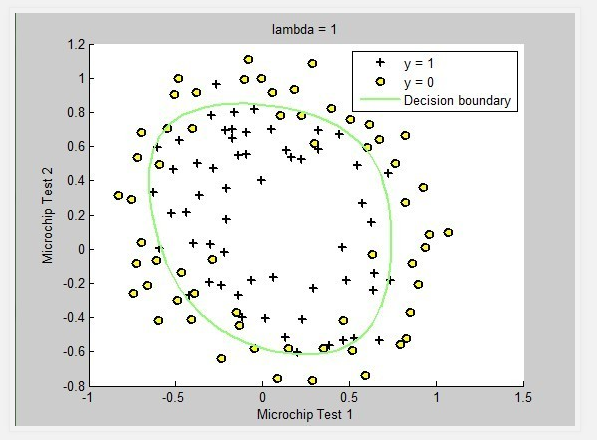
上图的 lambda = 0表示未做正则化,模型过于复杂(存在过拟合)
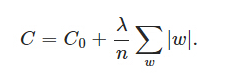 ,其中C0是代价函数,
,其中C0是代价函数,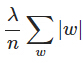 是L1正则项,lambda是正则化参数
是L1正则项,lambda是正则化参数
L2正则化(ridge):(待添加:权值衰减引入)
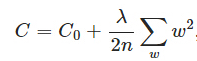 ,其中
,其中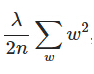 是L2正则项,lambda是正则化参数
是L2正则项,lambda是正则化参数
ElasticNet 正则化:
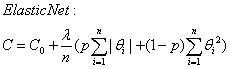
L1与L2以及ElasticNet 正则化的比较:
1.L1会趋向于产生少量的特征,而其他的特征都是0,而L2会选择更多的特征,这些特征都会接近于0。
2.Lasso在特征选择时候非常有用,而Ridge就只是一种规则化而已。
3.ElasticNet 吸收了两者的优点,当有多个相关的特征时,Lasso 会随机挑选他们其中的一个,而ElasticNet则会选择两个;并且ElasticNet 继承 Ridge 的稳定性.
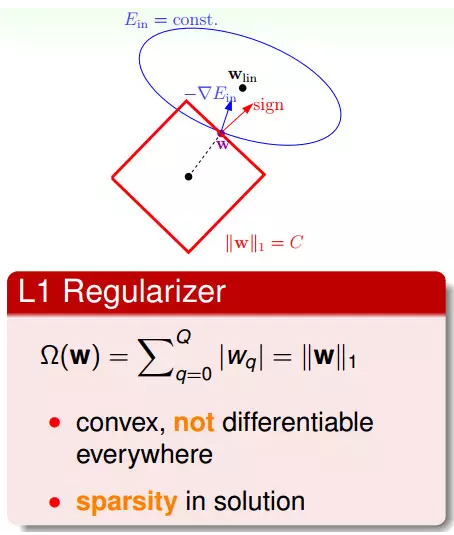
L1 Regularizer
L1 Regularizer是用w的一范数来算,该形式是凸函数,但不是处处可微分的,所以它的最佳化问题会相对难解一些。
L1 Regularizer的最佳解常常出现在顶点上(顶点上的w只有很少的元素是非零的,所以也被称为稀疏解sparse solution),这样在计算过程中会比较快。
L2 Regularizer
L2 Regularizer是凸函数,平滑可微分,所以其最佳化问题是好求解的。

参考链接:常见的距离算法和相似度(相关系数)计算方法中的Lp球
2.归一化 (Normalization)
2.1归一化的目的:
1)归一化后加快了梯度下降求最优解的速度;
2)归一化有可能提高精度。详解可查看
2.2归一化计算方法
2.3.spark ml中的归一化
newNormalizer(p: Double) ,其中p就是计算公式中的向量绝对值的幂指数
可以使用transform方法对Vector类型或者RDD[Vector]类型的数据进行正则化
下面举一个简单的例子:
scala> val dv: Vector = Vectors.dense(3.0,4.0)
dv: org.apache.spark.mllib.linalg.Vector = [3.0,4.0]
scala> val l2 = new Normalizer(2)
scala> l2.transform(dv)
res8: org.apache.spark.mllib.linalg.Vector = [0.6,0.8]
或者直接使用Vertors的norm方法:val norms = data.map(Vectors.norm(_, 2.0))
2.4 python中skelearn中的归一化
from sklearn.preprocessing import Normalizer
#归一化,返回值为归一化后的数据
Normalizer().fit_transform(iris.data)