摘要：
1.算法概述
2.算法推导
3.算法特性及优缺点
4.注意事项
5.实现和具体例子
6.适用场合
内容：
1.算法概述
最基本的LR模型适用于二分类(一般label是0,1)问题；这个模型以样本特征的线性组合sigma(theta * Xi)作为自变量，使用sigmoid函数将自变量映射到(0,1)上。
其中sigmoid函数为：
函数图形为： 其中sigmoid函数的导数是：
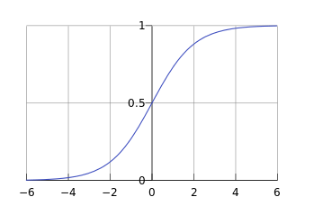
从而得到LR的模型函数为：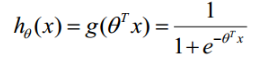
，其中
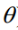待定。
2.算法推导
2.1 MLE(最大似然估计)求解参数的值
建立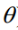的似然函数：
对上述函数求对数：
做下函数变换：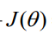
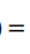
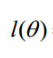
$ ext{从而得到LR的损失函数:} Loss(h_ heta(x_i),y_i)=frac{1}{m}sum_{i=1}^{m}(y_ilog(1+e^{- heta^{T}x_i})+(1-y_i)log(1+e^{ heta^{T}x_i})) $
注：LR的损失函数可以看作是负对数损失或者说模型推导过程就是一个使用极大对数似然法来估计参数的过程。
通过梯度下降法求最小值。θ的初始值可以全部为1.0，更新过程为：
求导：
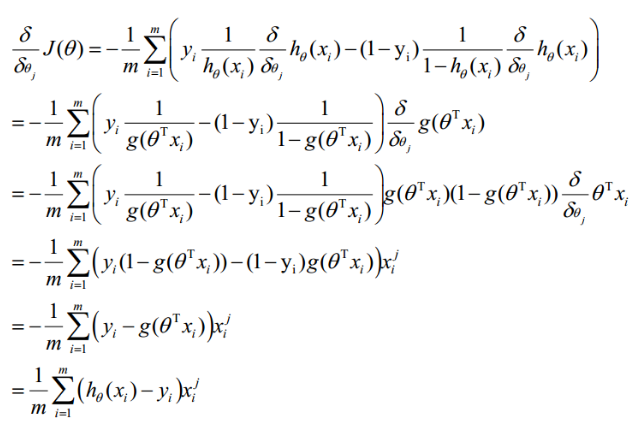
最终得到θ的迭代公式：
2.2 矩阵形式（矢量化）的解：
约定训练数据的矩阵形式如下，x的每一行为一条训练样本，而每一列为不同的特征取值：
g(A)的参数A为一列向量，所以实现g函数时要支持列向量作为参数，并返回列向量。由上式可知hθ(x)
-y可由
g(A)-y一次计算求得。
θ更新过程可以改为：
综上所述，Vectorization后θ更新的步骤如下：
（1）求A=X*θ(此处为矩阵乘法，X是（m,n+1）的矩阵，θ是n+1维列向量，A就是m维向量
（2）求E=g(A)-y（E、y是m维列向量）
（3）求 
2.4 多分类模型softmax regression
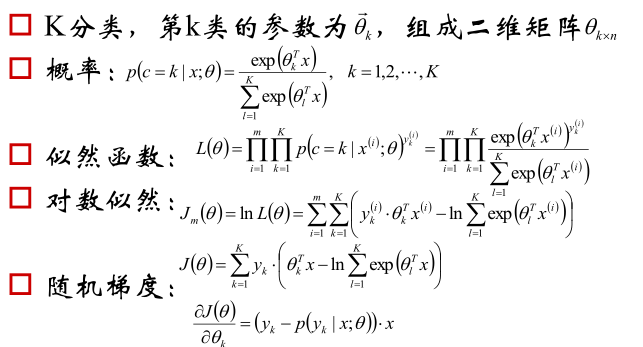
模型函数：
$ Loss(h_ heta(x_i),y_i)=frac{1}{m}sum_{i=1}^{m}(y_ilog(1+e^{- heta^{T}x_i})+(1-y_i)log(1+e^{ heta^{T}x_i})) $
损失函数：
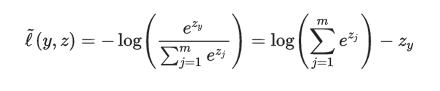，其中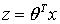
3.算法特性及优缺点
LR分类器适用数据类型：数值型和标称型数据。
可用于概率预测，也可用于分类。
其优点是计算代价不高，易于理解和实现；其缺点是容易欠拟合，分类精度可能不高。
各feature之间不需要满足条件独立假设(相比NB)，但各个feature的贡献是独立计算的(相比DT)。
相比DT，注重一个样本的总体特征表现
4.注意事项
学习率：值太小则收敛慢，值太大则不能保证迭代过程收敛（迈过了极小值）。
归一化：多维特征的训练数据进行回归采取梯度法求解时其特征值必须做scale，确保特征的取值范围在相同的尺度内计算过程才会收敛
最优化方法选择：L-BFGS（限制内存-拟牛顿迭代）收敛速度快；
正则化：L1正则化可以选择特征，去除共线性影响；损失函数中使用了L1正则化，避免过拟合的同时输出稀疏特征；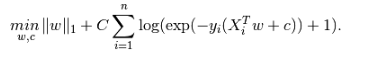
(来自http://scikit-learn.org/stable/modules/linear_model.html#logistic-regression)
离散化：逻辑回归属于广义线性模型，表达能力受限；单变量离散化为N个后，每个变量有单独的权重，相当于为模型引入了非线性，能够提升模型表达能力，加大拟合。
（知乎问答：连续特征的离散化：在什么情况下将连续的特征离散化之后可以获得更好的效果？）
5.实现和具体例子
Logistic回归的主要用途：
6.适用场合
是否支持大规模数据：支持，并且有分布式实现
特征维度：可以很高
是否有 Online 算法:有（参考自）
特征处理：支持数值型数据，类别型类型需要进行0-1编码；需要归一化