POJ2391(最大流Isap+Floyd+二分)

题意：给出一些牛棚，开始牛棚边有一些牛，牛棚之间有路相连，走一条路会花费固定的时间。牛在牛棚边吃草，下雨时牛得躲进牛棚，每个牛棚容量有限。
求在所有牛都能进牛棚时最少需要多少时间。

这题和POJ2112相似,不过这题要拆点,把每个点拆成两个点,如果直接连原图中的点，是不对的。网上找了大神的图

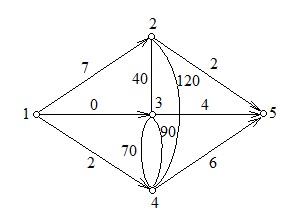
当二分到T = 70的时候，显然我们只加入了(2, 3)和(3, 4)两条无向边，因为只有这两对点间的最短距离小于等于70。但是从图中也可以看出，由于没有拆点，点2也可以通过这两条边到达点4，而实际上这是不允许的。也就是说我们所加的限制条件没有起到作用。由此可见，只有拆点才是正确的做法。

然后这题还要注意64位。。

详情见代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
using namespace std;
#define N 450
#define M 88888
typedef long long lld;
typedef unsigned long long u64;
const int inf= 0x7fffffff;
const lld dis_inf= 10000000000000000LL;
struct Edge
{
    int v,w,next;
    Edge(){}
    Edge(int V,int W,int NEXT):v(V),w(W),next(NEXT){}
}edge[M];
int pre[N],cur[N],dis[N],gap[N];
int size,head[N];
int F,P,nv,num,s,e;
lld map[N][N];
int cow[N],col[N];
lld mid;
void InsertEdge(int u,int v,int w) // 建边 
{
    edge[size] = Edge(v,w,head[u]);
    head[u] = size++;
    edge[size] = Edge(u,0,head[v]);
    head[v] = size++;
}
void Floyd() //Floyd求两点间的最短距离 
{
    for(int k=1; k<=F; k++)
    {
        for(int i=1; i<=F; i++)
        {
            if(k==i||map[i][k]==dis_inf) continue;
            for(int j=1; j<=F; j++)
            {
                if(k==j||map[k][j]==dis_inf) continue;
                if(map[i][j] > map[i][k]+map[k][j])
                 map[i][j] = map[i][k] + map[k][j];
            }
        }
    }
}
void Init() //建图 
{
    size = 0;
    memset(head,-1,sizeof(head));
    for(int i=1; i<=F; i++)
    {
        for(int j=1; j<=F; j++)
        {
            if(map[i][j] <= mid) 
            InsertEdge(i,F+j,inf); //如果两点间的距离<=mid,两点间建条权值为inf的边，表示这条边可以容纳无数奶牛 
        }
        InsertEdge(s,i,col[i]); //对源点到每个草地建边，权值为草地的容量 
        InsertEdge(i+F,e,cow[i]); //对每个草地的拆点到汇点建边，权值为草地现有的牛 
    }
}
int Isap(int st,int ed,int n) { //Isap模板 
    for(int i=0; i<=n; i++) {
        cur[i] = head[i];
        gap[i] = dis[i] = 0;
    }
    int u = pre[st] = st;
    int aug = inf ,maxflow = 0;
    while(dis[st] < n) {
loop:
        for(int &i=cur[u]; i!=-1; i=edge[i].next) {
            int v = edge[i].v;
            if(edge[i].w && dis[u] == dis[v] + 1) {
                aug = min(aug,edge[i].w);
                pre[v] = u;
                u = v;
                if(v==ed) {
                    maxflow += aug;
                    for(u=pre[u]; v!=st; v=u,u=pre[u]) {
                        edge[cur[u]].w -= aug;
                        edge[cur[ u]^1].w += aug;
                    }
                    aug = inf;
                }
                goto loop;
            }
        }
        int mindis = n;
        for(int i=head[u]; i!=-1; i=edge[i].next) {
            int v = edge[i].v;
            if(edge[i].w && dis[v]<mindis) {
                cur[u] = i;
                mindis = dis[v];
            }
        }
        if(--gap[dis[u]]==0) break;
        gap[dis[u] = mindis+1]++;
        u = pre[u];
    }
    return maxflow;
}

int main()
{
    while(scanf("%d%d",&F,&P)!=EOF)
    {
        s = 0 ; e = 2*F+1 ; nv = e+1;
        //源点，汇点，节点数 
        num = 0; //奶牛总数 
        for(int i=1; i<=F; i++)
        {
            scanf("%d%d",&cow[i],&col[i]);
            num += cow[i];
        }
        for(int i=1; i<=F; i++) 
        for(int j=1; j<=F; j++) 
        map[i][j]= i==j ? 0 : dis_inf;
        lld l = 0 ,r = 0; //二分的左右界 
        int u,v,w;
        for(int i=1; i<=P; i++)
        {
            scanf("%d%d%d",&u,&v,&w);
            r += w;
            if(w < map[u][v]) map[u][v] = map[v][u] = w;
        }
        Floyd();
        int flag = 1; //标志是否找到合适的距离 
        while(l <= r)
        {
            mid = l + (r-l)/2;
            Init();
            if(Isap(s,e,nv)==num) 
            {
                r = mid-1;
                flag = 0;
            }
            else l = mid + 1;
        }
        if(flag) printf("-1
");
        else printf("%lld
",l);
    }
    return 0;
}