题目描述
lxhgww最近收到了一个01序列,序列里面包含了n个数,这些数要么是0,要么是1,现在对于这个序列有五种变换操作和询问操作:
0 a b 把[a, b]区间内的所有数全变成0
1 a b 把[a, b]区间内的所有数全变成1
2 a b 把[a,b]区间内的所有数全部取反,也就是说把所有的0变成1,把所有的1变成0
3 a b 询问[a, b]区间内总共有多少个1
4 a b 询问[a, b]区间内最多有多少个连续的1
对于每一种询问操作,lxhgww都需要给出回答,聪明的程序员们,你们能帮助他吗?
输入格式
输入数据第一行包括2个数,n和m,分别表示序列的长度和操作数目
第二行包括n个数,表示序列的初始状态
接下来m行,每行3个数,op, a, b,(0<=op<=4,0<=a<=b<n)表示对于区间[a, b]执行标号为op的操作
输出格式
对于每一个询问操作,输出一行,包括1个数,表示其对应的答案
输入输出样例
输入
10 10
0 0 0 1 1 0 1 0 1 1
1 0 2
3 0 5
2 2 2
4 0 4
0 3 6
2 3 7
4 2 8
1 0 5
0 5 6
3 3 9
输出
5
2
6
5
说明/提示
对于30%的数据,1<=n, m<=1000
对于100%的数据,1<=n, m<=100000
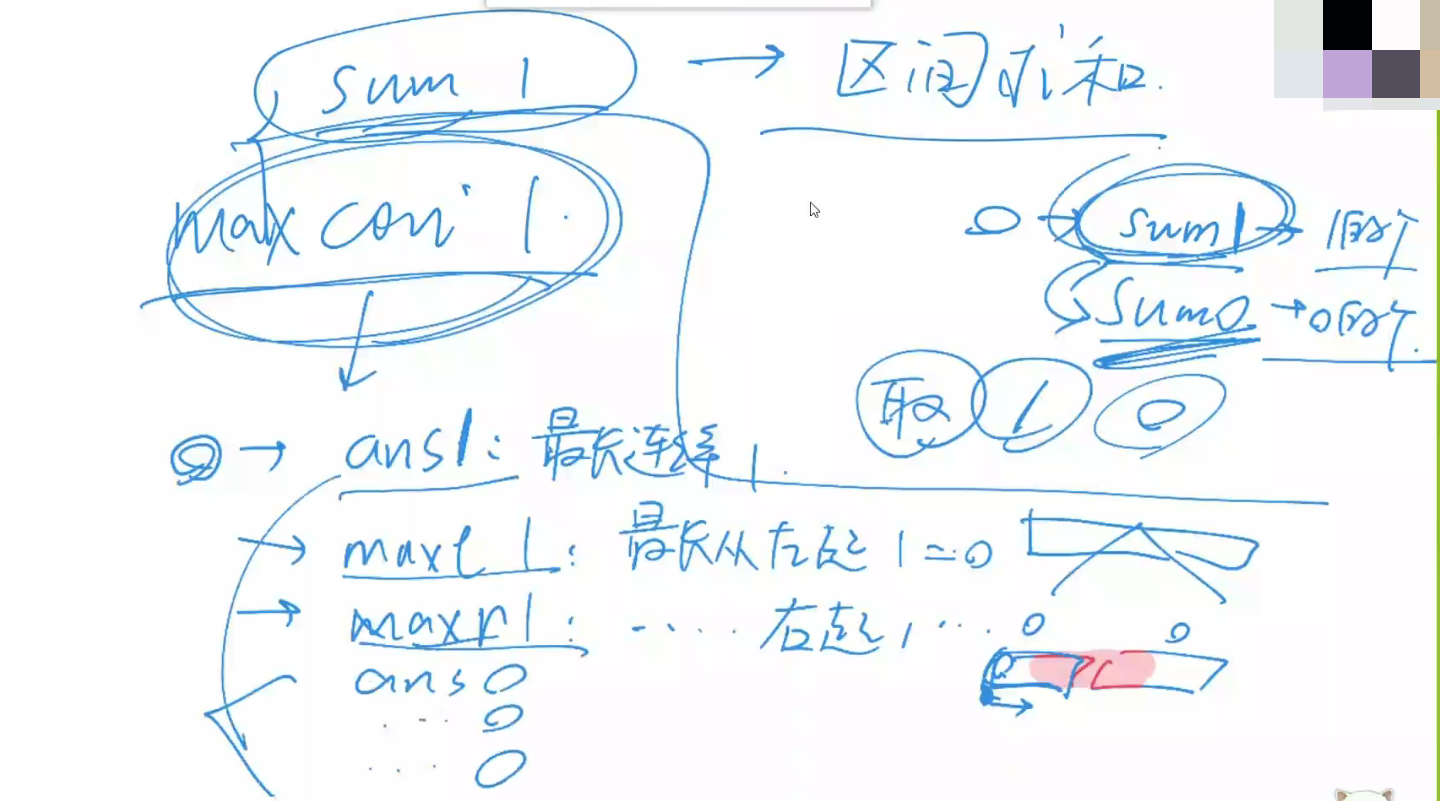
询问总共有多少个1 可以直接维护区间和sum来解决
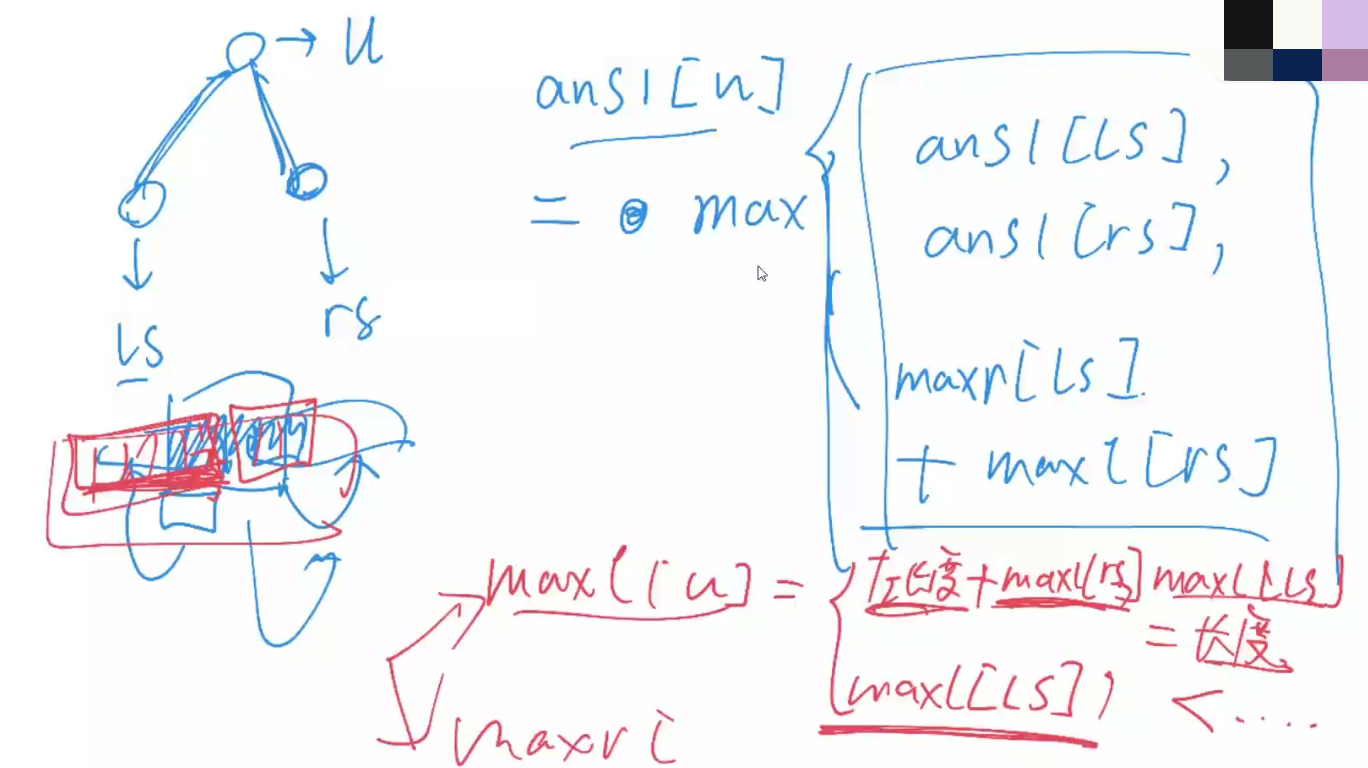
询问最多有多少个连续的1 可以考虑维护 一个节点对应区间的 maxl 与 maxr;分别代表左边开始最多的连续1的数目和右边开始最多的连续的1的数目
因为还有把0和1交换的操作
所以同时再维护一下一个区间的0的个数和sum0,以及连续的0的数目
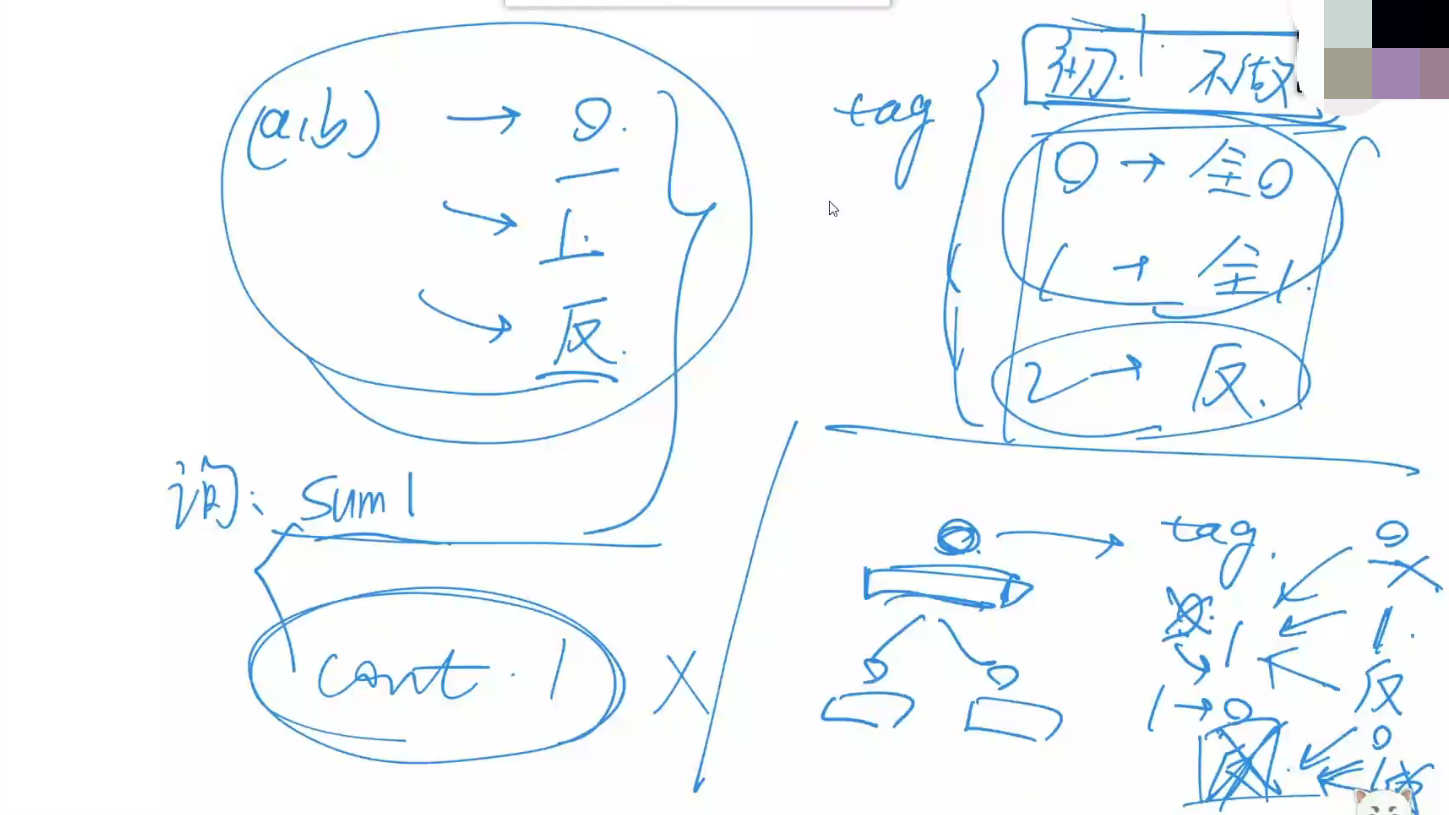
tag的话 一个tag表示置0、置1或当前没有置01的操作 另一个tag表示翻转区间的0和1 遇到翻转时,可以直接修改置01的tag,遇到置01时,直接删除掉翻转tag,这里的更新操作是什么可以思考一下
附上dalao代码 https://www.luogu.org/blog/tanrui-2960967961/solution-p2572
#include <bits/stdc++.h> //#define Int register int #define MAXN 100005 using namespace std; int n,m,a[MAXN]; struct node{ int l,r,sum1,max1,max0,maxl0,maxr0,maxl1,maxr1,lazy1; bool overturn; int size (){ return r - l + 1; } }tree[MAXN << 2]; int Max (int a,int b,int c){ if (a >= b && a >= c) return a; else if (b >= a && b >= c) return b; else if (c >= a && c >= b) return c; } void Push_up (int i){ tree[i].sum1 = tree[i << 1].sum1 + tree[i << 1 | 1].sum1; tree[i].max1 = Max (tree[i << 1].max1,tree[i << 1 | 1].max1,tree[i << 1].maxr1 + tree[i << 1 | 1].maxl1); tree[i].max0 = Max (tree[i << 1].max0,tree[i << 1 | 1].max0,tree[i << 1].maxr0 + tree[i << 1 | 1].maxl0); //下面这些是看子区间长度够不够长来更新 tree[i].maxl0 = (tree[i << 1].maxl0 == tree[i << 1].size() ? tree[i << 1].size() + tree[i << 1 | 1].maxl0 : tree[i << 1].maxl0); //如果左儿子全是0,那该点最长连续的0长度为左儿子长加右儿子以左端点开始的连续的0长度 tree[i].maxl1 = (tree[i << 1].maxl1 == tree[i << 1].size() ? tree[i << 1].size() + tree[i << 1 | 1].maxl1 : tree[i << 1].maxl1); //1同理 tree[i].maxr0 = (tree[i << 1 | 1].maxr0 == tree[i << 1 | 1].size() ? tree[i << 1 | 1].size() + tree[i << 1].maxr0 : tree[i << 1 | 1].maxr0); tree[i].maxr1 = (tree[i << 1 | 1].maxr1 == tree[i << 1 | 1].size() ? tree[i << 1 | 1].size() + tree[i << 1].maxr1 : tree[i << 1 | 1].maxr1); //反过来从右儿子右端点的情况也一样 } void Maintain (int i){ tree[i].overturn = 0;//如果你都区间赋值了,就不用管翻转了 //???? if (tree[i].lazy1 == 1){//区间赋值为零 tree[i].max0 = tree[i].maxl0 = tree[i].maxr0 = tree[i].size(); //连续的0最长长度变为树的长度 tree[i].max1 = tree[i].maxl1 = tree[i].maxr1 = tree[i].sum1 = 0; //连续的0最长长度变为0 } else if (tree[i].lazy1 == 2){//区间赋值为1 tree[i].max0 = tree[i].maxl0 = tree[i].maxr0 = 0;//与上面同理 tree[i].max1 = tree[i].maxl1 = tree[i].maxr1 = tree[i].sum1 = tree[i].size(); } } void Mainflip (int i){//区间翻转 tree[i].sum1 = tree[i].size() - tree[i].sum1; //该点的值变为长度减去原来的值(因为只有0和1,这样就相当于0全变成1,1全变成0) swap (tree[i].max1,tree[i].max0);//最大连续0和最大连续1交换 swap (tree[i].maxl0,tree[i].maxl1);//左儿子的最大连续0和最大连续1交换 swap (tree[i].maxr0,tree[i].maxr1);//右儿子的最大连续0和最大连续1交换 } void Push_down (int i){ //标记下传 if (tree[i].lazy1 == 1){//赋值为0 tree[i << 1].lazy1 = tree[i << 1 | 1].lazy1 = 1;//将标记传给左右儿子 Maintain (i << 1); Maintain (i << 1 | 1); tree[i].lazy1 = 0;//赋完值清除标记 } else if (tree[i].lazy1 == 2){//赋值为1 tree[i << 1].lazy1 = tree[i << 1 | 1].lazy1 = 2; Maintain (i << 1); Maintain (i << 1 | 1); tree[i].lazy1 = 0; } if (tree[i].overturn){//如果需要翻转 tree[i << 1].overturn ^= 1; //就是用1,不能用0 tree[i << 1 | 1].overturn ^= 1;//这里翻转懒标记取反就好了 Mainflip (i << 1); Mainflip (i << 1 | 1); tree[i].overturn = 0; } } void Build (int i,int l,int r){ tree[i].l = l,tree[i].r = r; if(l == r){ //该节点只有一个值的话 tree[i].max1 = a[l]; tree[i].max0 = !a[l];//0 //cout<<!a[l]<<endl; tree[i].maxl0 = tree[i].maxr0 = !a[l]; tree[i].sum1 = tree[i].maxl1 = tree[i].maxr1 = a[l]; return ; } int mid = (l + r) >> 1; Build (i << 1,l,mid); Build (i << 1 | 1,mid + 1,r); Push_up (i); } void Update (int i,int l,int r,int flag){//区间赋值为0或者1 if (tree[i].l > r || tree[i].r < l) return;//区间不符,直接返回,不改了 if (tree[i].l >= l && tree[i].r <= r){ tree[i].lazy1 = flag + 1; /*flag记录原操作(因为lazy=0时为赋值0的操作,而清楚标记时将标记变成了0, Maintain函数中便将1当做赋0,2当做赋1)*/ Maintain (i); return ; } Push_down (i); Update (i << 1,l,r,flag); Update (i << 1 | 1,l,r,flag); Push_up (i); } void Flip (int i,int l,int r){//区间翻转 if (tree[i].l > r || l > tree[i].r) return; if (tree[i].l >= l && tree[i].r <= r){ tree[i].overturn ^= 1;//就是搞不懂为什么要翻转标记 Mainflip (i); return; } Push_down (i); Flip (i << 1,l,r); Flip (i << 1 | 1,l,r); Push_up (i); } int query1 (int i,int l,int r){//查询总的1的个数 if (tree[i].l > r || l > tree[i].r) return 0; if (tree[i].l >= l && tree[i].r <= r) return tree[i].sum1; Push_down (i); return query1 (i << 1,l,r) + query1 (i << 1 | 1,l,r); } node query2 (int i,int l,int r){//最长的连续的1的长度 if (l == tree[i].l && r == tree[i].r) return tree[i]; Push_down (i); int mid = (tree[i].l + tree[i].r) >> 1; if (r <= mid) return query2 (i << 1,l,r);//在左区间 else if (mid < l) return query2 (i << 1 | 1,l,r);//在右区间 else{ node ls = query2 (i << 1,l,mid),rs = query2 (i << 1 | 1,mid + 1,r),tmp;//递归 tmp.l = tree[i].l,tmp.r = tree[i].r; tmp.maxl1 = (ls.maxl1 == ls.size() ? ls.maxl1 + rs.maxl1 : ls.maxl1); tmp.maxr1 = (rs.maxr1 == rs.size() ? rs.maxr1 + ls.maxr1 : rs.maxr1);//把两边的像Pushup揉成一坨 tmp.max1 = Max (ls.max1,rs.max1,ls.maxr1 + rs.maxl1);//统计最大值 return tmp; } } void read (int &x){ x = 0;char c = getchar();int f = 1; while (c < '0' || c > '9') {if (c == '-') f = -f;c = getchar();} while (c >= '0' && c <= '9') {x = (x << 3) + (x << 1) + c - '0';c = getchar();} x *= f; return ; } void write (int x){ if (x < 0){x = -x;putchar ('-');} if (x > 9) write (x / 10); putchar (x % 10 + '0'); } signed main(){ read (n),read (m); for (register int i = 1;i <= n;++ i) read (a[i]); Build (1,1,n); for (register int i = 1;i <= m;++ i){ int opt,l,r; read (opt),read (l),read (r); l ++,r ++; if (opt <= 1) Update (1,l,r,opt); else if (opt == 2) Flip (1,l,r); else if (opt == 3) write (query1 (1,l,r)),putchar (' '); else if (opt == 4) write (query2 (1,l,r).max1),putchar (' '); } }