前言
树的遍历分为:
1.深度优先遍历
2.广度优先遍历
深度优先遍历:
1.前序遍历
2.中序遍历
3.广序遍历
广度优先遍历:
层序遍历
深度优先遍历
如图:
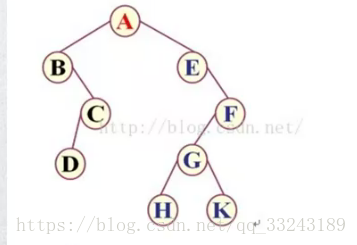
前序遍历
前序遍历的规则为:根节点、左子树、右子树
根据规则,第一个点即为根节点:
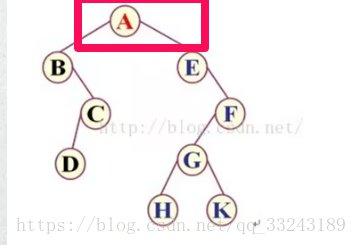
第一个为A。
A 有左子树:左子树的第一个节点又为左子树的根节点,所以为AB

接下来,B没有左子树,根据规则根节点、左子树、右子树,第三优先级为右子树。
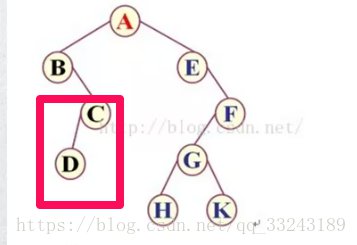
c右子树的根节点为C,所以为ABC,然后C有左子树,且根节点为D,结果为ABCD。
A的左子树就遍历完毕了,接下来遍历A的右子树。
A的右子树的根节点为E,结果为ABCDE。在E右子树中,E没有左子树,所以遍历右子树,E右子树的根节点为F,所以结果为ABCDEF。
F子树有G左子树,G为根节点,结果为ABCDEFG。G子树有左子树,所以结果为ABCDEFG,然后H为叶子节点,回到G上,G有右子树,且只有一个右根节点K,结果为ABCDEFGHK。
中序遍历
中序遍历比较重要,规则为:左子树,根节点,右子树。
一切都是从根节点开始的。
从A开始,因为A有B左子树,所以A不是第一个点。
B子树没有左子树,所以B为根节点,结果为B。

B子树的根节点遍历完毕,就到右子树了。右子树C有左节点,D子树只有根节点,结果为:BD。
然后回到C子树,C遍历了左子树,那么优先级为根节点,根节点为C,结果为BDC。
B子树就遍历完毕了。A的左子树遍历完毕,优先级为根节点,根节点为A,结果为BDCA。
A子树的左子树与根节点遍历完毕,那么优先级为右子树。
右子树的根节点为E,E没有左子树,优先级为根节点,那么结果为BDCAE。
E的左子树,根节点遍历完毕,那么开始遍历F右子树。
F右子树,有左子树,G左子树。G又有H左子树,且H左子树只有根节点——H,结果为:BDCAEH。
然后回到了G,G的左子树遍历完毕,G为G左子树的根节点,结果为:BDCAEHG。同理,G子树没有了左子树,根节点,结果为:BDCAEHGK。
回到了F子树,F子树的左子树遍历完毕,优先级为F,结果为:BDCAEHGKF。
后序遍历
规则:左子树,右子树,根节点
同理,结果为:DCBHKGFEA。
广度优先遍历
层序遍历
我们知道其实一切都是从根节点开始,在这里是A。
在这种排序遍历中,和一个队列有关。
先将A进入队列,队列中为:A;
然后A出队列,输出A,左右子树的B,E进入队列,队列中为:BE。
然后B出队列,输出AB,C进入队列,队列中为:EC。
然后E出队列,输出为ABE,F进入队列,队列中为:CF。
然后c出队列,输入为ABEC,D进入队列,队列中为:FD。
然后F出队列,输入为ABECF,G进入队列,队列为:DG.
然后D出队列,然后输入为ABECFD,队列为:G
然后G出队列,然后输入为ABECFDG,队列为:HK
然后HK分别出队列,输出为ABECFDGHK。
这种原理非常简单,就是每个都会遍历到,将其子节点找出。
总结
其实遍历关键之处在于能遍历完,至于怎么遍历呢,就是一个纯粹的思考过程。