[学习笔记] EM算法、GMM

EM算法、GMM - Demo

Intro

这一节学习内容为概率图模型里的一节，因为下午在跑程序手里也没什么事情干，写个EM的demo记录一下。本文也不是来推导过程的，只是方法和代码记录，推导请看其他博客。

GMM

概率图模型跳不过的一章就是高斯混合模型，高斯混合模型是由多个高斯分布以一定权重组成的模型，其概率密度函数等于各高斯模型的概率密度函数加权求和。

一般地，每个高斯分布的概率密度为：

[N(x|mu_k,sigma_k) = frac{1}{sqrt{2pi}sigma} exp(-frac{(x-mu_k)^2}{2sigma_k^2}) ]

其中k代表第k个高斯分布，因此GMM的概率分布为：

[p(x) = sum_{k=1}^K pi_kN(x|mu_k,sigma_k) ]

其中(sum_{k=1}^{K}{pi_k} = 1)且(pi_k geq 0).

GMM的一个基本问题就是选用高斯混合模型对数据进行建模，那么模型的参数如何获得呢？

一个GMM的参数仅由一组(、、(pi、mu、sigma))决定，所以我们要估计的参数就是这三个。其涉及的问题是包含隐变量的参数的求解过程，如果模型不含隐变量，直接用最大似然然后求个导就能解决，但是现在模型含有隐变量，也就意味着求导的过程极其复杂，一个比较好的方法是通过EM算法来进行参数估计。

关于GMM的简介就到这里，网上有很多关于GMM的介绍，也非常通俗易懂，不多赘述。

EM

EM算法是一个求解带隐变量的模型的参数常用的方法，其通过最大化训练集的边界似然，迭代更新参数。

过程为：

1. 先初始化随机参数
2. E步：固定参数求解后验概率
3. M步：固定后验概率，优化求解证据下界对应的参数。
4. 重复进行直到收敛。

对于GMM模型而言，要求其参数就是按照上面的步骤进行。但在开始之前，我们要先生成给定分布的样本，即采样。采样步骤为：

1. 按照(、pi_1、pi_2 dots pi_K)的的分布随机选择一个高斯分布
2. 假设选择了第k个高斯分布，按照(N(x|mu_k,sigma_k))的分布采样一个样本(高斯分布的采样计算机可以实现)

E步

固定(mu,sigma)，计算后验概率分布(p(z^{(n)}|x^{(n)}))

[gamma_{nk} xlongequal[]{def} p(z^{(n)} = k|x^{(n)}) \=frac{p(z^{(n)})p(x^{(n)}|z^{(n)})}{p(x^{(n)})} \=frac{p(z^{(n)})p(x^{(n)}|z^{(n)})}{sum_{k=1}^{K}pi_kN(x^{(n)}|mu_k,sigma_k)} ]

用上式(gamma_{nk})表示第n个样本对第k个高斯分布的后验概率，其用(N imes K)的矩阵表示。

M步

在已知后验概率的情况下，最大化边际似然(p(x|mu,sigma)),即最大化对数似然:

[log(p(x|mu,sigma)) = sum_{n=1}^{N} log sum_{k=1}^{K} q(z)frac{p(x^{(n)},z^{(n)}=k|mu_k,sigma_k)}{p(z^{(n)} = k)}\geq sum_{n=1}^{N}sum_{k=1}^{K} log space q(z)frac{p(x^{(n)},z^{(n)}=k|mu_k,sigma_k)}{p(z^{(n)} = k)}\xlongequal[]{def} ELBO(q,x|mu,sigma) \ ]

其中(q(z) = p(z^{(n)}=k)),ELBO通过不等式定义为函数下界，所以我们要求的其实是对数似然的下界。

[max_{mu,sigma,pi} ELBO(gamma,D|pi,mu,sigma)\s.t. sum_{k=1}^{K} = 1 ]

D为训练集，(gamma)为后验分布。

利用拉格朗日法求解后有如下更新的结论：

[pi_k leftarrow frac{N_k}{N}\mu_k leftarrow frac{1}{N_k}sum_{n=1}^Ngamma_{nk}x^{(n)}\sigma_k = sqrt{frac{1}{N_k}sum_{n=1}^N gamma_{nk}(x^{(n) - u_k})^2} ]

其中(N_k = sum_{n=1}^N gamma_{nk})

Coding

'''
@Descripttion: This is Aoru Xue's demo, which is only for reference.
@version: 
@Author: Aoru Xue
@Date: 2019-12-30 20:46:28
@LastEditors  : Aoru Xue
@LastEditTime : 2019-12-31 00:03:01
'''
from matplotlib import pyplot as plt
import numpy as np
import random
import pickle
# 代码里的循环运算可以矩阵优化，有兴趣且需要请自行优化，高维需要修改部分代码。为保证例子简单，故以一维高斯分布为例。

class GMM():
    def __init__(self,pi,mu,sigma,samples): # 生成一个一维高斯混合分布
        self.x = np.zeros(shape = (samples,))
        for i in range(samples):
            idx = np.random.choice(range(pi.shape[0]),p=pi)
            self.x[i] = np.random.normal(mu[idx],sigma[idx])
        self.mu = np.random.randn(mu.shape[0])
        self.sigma = np.ones(sigma.shape[0])
        self.pi = np.ones(sigma.shape) / sigma.shape[0]
    @staticmethod
    def gausian_probablity(x,mu,sigma):
        return 1. / np.sqrt(2 * np.pi)/sigma * np.exp(- (x - mu)**2 / 2 / sigma**2)
    def EM_method(self,):
        post_probability = np.zeros((self.x.shape[0],self.pi.shape[0]),dtype = np.float) # (N,K)
        
        for _ in range(100):
            # E
            for n in range(post_probability.shape[0]):
                for k in range(post_probability.shape[1]):
                    post_probability[n,k] = self.gausian_probablity(self.x[n],self.mu[k],self.sigma[k]) * self.pi[k]
            
            post_probability = post_probability / np.sum(post_probability,axis = 1,keepdims=True) # 后验概率
            

            # M
            N_k = np.sum(post_probability,axis = 0)
            
            for k in range(post_probability.shape[1]):
                self.pi[k] = N_k[k] / post_probability.shape[0]
                self.sigma[k] = np.sqrt(1./N_k[k] * np.sum(post_probability[:,k] * (self.x - self.mu[k])**2))
                self.mu[k] = 1. / N_k[k] * np.sum(post_probability[:,k] * self.x) # (N,1) * (N,1)
        return self.pi,self.mu,self.sigma
def draw(pis, mus, sigmas,color="r", tag="real"):
    x_min = mus - 3 * mus
    x_max = mus + 3 * mus
    x_bottom = x_min.min()
    x_top = x_max.max()
    x_array = np.linspace(x_bottom, x_top, 200)
    y_array = np.zeros(200, dtype=float)
    for pi, mu, sigma in zip(pis, mus, sigmas):
        y_array = y_array + pi * gmm.gausian_probablity(x_array, mu, sigma)
    plt.figure(0)
    plt.plot(x_array, y_array, color=color, label=tag)
    plt.legend()
    plt.xlim([x_array.min(), x_array.max()])

if __name__ == "__main__":
    pi = np.array([0.1,0.3,0.6])
    mu = np.array([-3,1,4])
    sigma = np.array([1,1,1])
    gmm = GMM(pi = pi,mu = mu,sigma = sigma,samples = 5000)
    plt.figure(0)
    plt.hist(gmm.x, bins=200, density=True)
    plt.plot()
    draw(pi, mu, sigma, color="r", tag="real")
    

    pi_,mu_,sigma_ = gmm.EM_method()
    draw(pi_, mu_, sigma_, color="g", tag="estimated")
    plt.show()
    
    

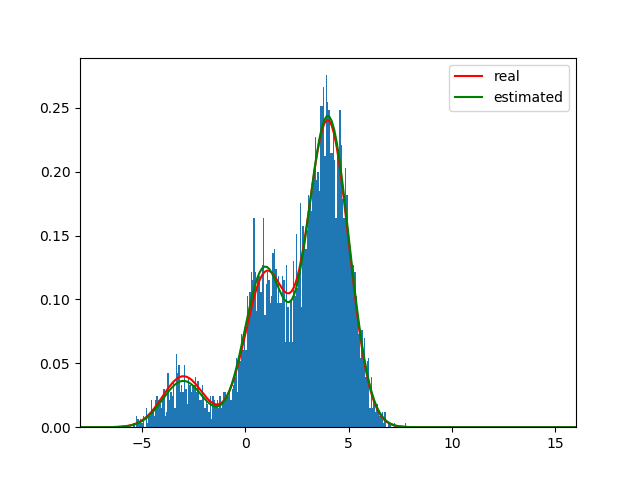
Visualization