一、平衡二叉树的定义
对一棵查找树(search tree)进行查询/新增/删除 等动作, 所花的时间与树的高度h 成比例, 并不与树的容量 n 成比例。如果可以让树维持矮矮胖胖的好身材, 也就是让h维持在O(lg n)左右, 完成上述工作就很省时间。能够一直维持好身材, 不因新增删除而长歪的搜寻树, 叫做balanced search tree(平衡树)。
【百度百科】平衡二叉树(Balanced Binary Tree)具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。
平衡二叉树一般是一个有序树,它具有二叉树的所有性质,其遍历操作和二叉树的遍历操作相同。但是由于其对二叉树施加了额外限制,因而其添加、删除操作都必须保证平衡二叉树的因子被保持。
二、树的左旋和右旋是怎么玩的?
动图体会一下:参考自最容易懂得红黑树
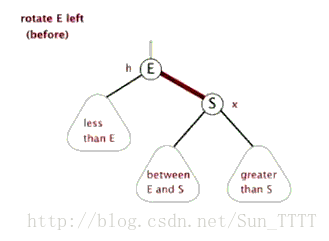
左旋代码:

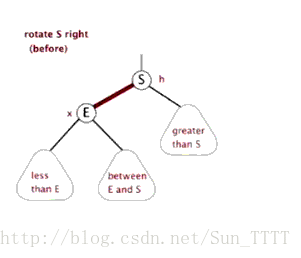
右旋代码:

三、节点失衡后的调整
平衡二叉树中引入了一个概念:平衡二叉树节点的平衡因子,它指的是该节点的两个子树,即左子树和右子树的高度差,即用左子树的高度减去右子树的高度,如果该节点的某个子树不存在,则该子树的高度为0,如果高度差的绝对值超过1就要根据情况进行调整。
平衡的调整共有四种情况:分别为LL,LR,RR,RL。
下面我们通过不断插入数据来说明几种不同的旋转方式:
注意:橘黄色的结点为旋转中心,黑色结点的为离插入结点最近的失衡结点。
(1)LR型
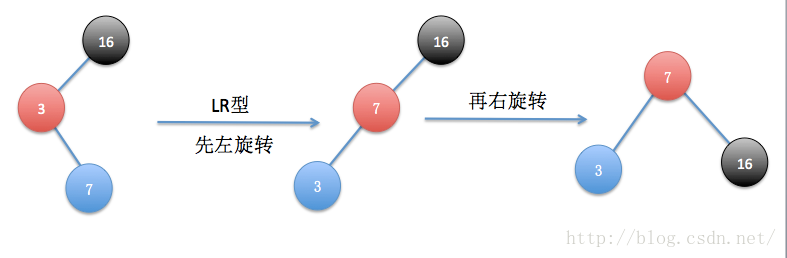
简单说明:最开始插入数据16,3,7后的结构如上图所示,结点16失去了平衡,3为16的左孩子,7为失衡结点的左孩子的右孩子,所以为LR型,接下来通过两次旋转操作复衡,先通过以3为旋转中心,进行左旋转,结果如图所示,然后再以7为旋转中心进行右旋转,旋转后恢复平衡了。
(2)LL型
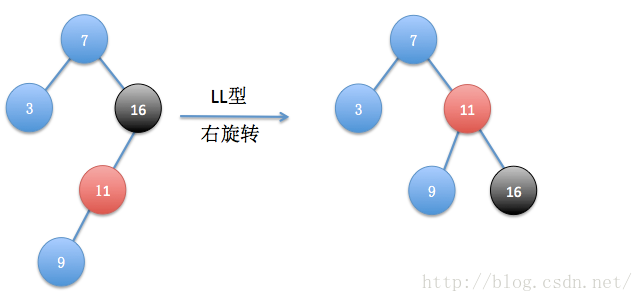
简单说明:在上面恢复平衡后我们再次插入数据11和9,发现又失去平衡了,这次失衡结点是16,11是其左孩子,9为其失衡结点的左孩子的左孩子,所以是LL型,以失衡结点的左孩子为旋转中心进行一次右旋转即可。
(3)RR型

简单说明:进一步插入数据26后又再次失衡了,失衡结点为7,很明显这是RR型,以失衡结点的右孩子为旋转中心左旋转一次即可。
(4)RL型
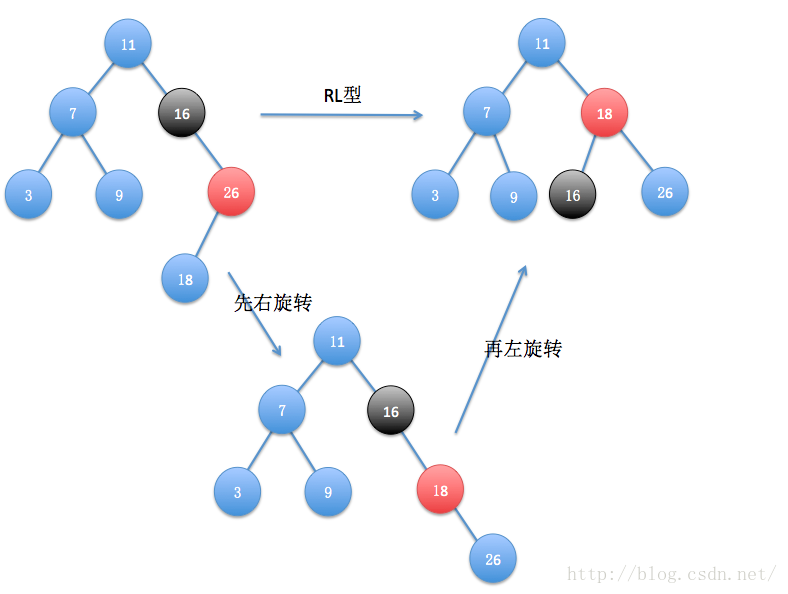
再插入18后又再次失衡了,失衡结点为16,26为其右孩子,18为其右孩子的左孩子,为RL型,以失衡结点的右孩子为旋转中心,进行一次右旋转,然后再次已失衡结点的右孩子为旋转中心进行一次左旋转变恢复了平衡。
小总结:
这就是4种失衡后调整的旋转方式,其实只有两种,RR和LL,RL和LR本质上是一样的。下面我们再次插入数据14,15,完成我们最后数据的插入操作:
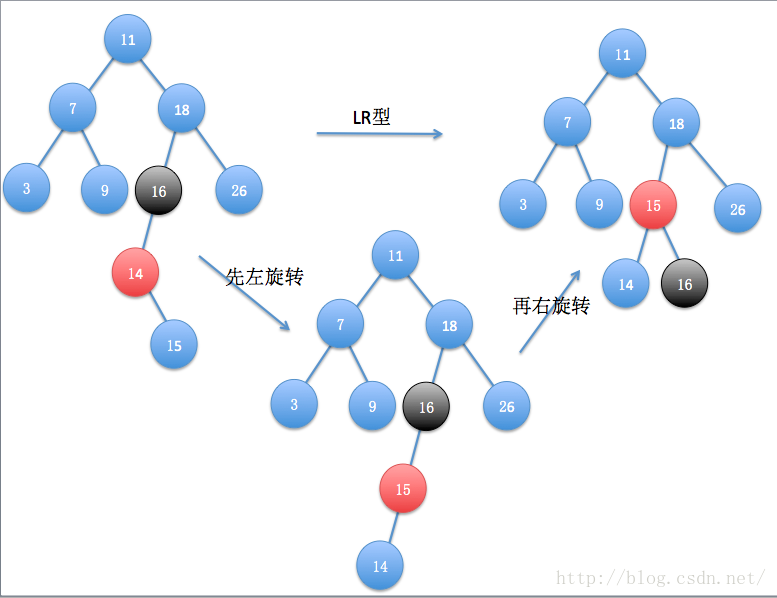
又是一次LR型,按前面操作就可以了。
四、应用场景
这个数据结构类似于双向链表,任意插入元素时都会自动排序,红黑树和平衡二叉树都使二叉树尽量平衡,从而使查询时和二分法类似。它适合的场合主要是:
- 需要时刻保证列表元素的有序排列;
- 需要频繁的增删和查询操作;
- 属于双向迭代器,不能随机访问任意元素;
五、总结
个人觉得,这一章还是比较难于理解的,失衡后如何进行旋转还需要结合图片细细体会。
平衡二叉树主要优点集中在快速查找。
我的微信公众号:架构真经(id:gentoo666),分享Java干货,高并发编程,热门技术教程,微服务及分布式技术,架构设计,区块链技术,人工智能,大数据,Java面试题,以及前沿热门资讯等。每日更新哦!

参考资料:
- https://www.cnblogs.com/shixiangwan/p/7530015.html
- https://blog.csdn.net/wannuoge4766/article/details/83998377
- https://blog.csdn.net/qq_25940921/article/details/82183093
- https://blog.csdn.net/u014634338/article/details/42465089
- https://blog.csdn.net/sun_tttt/article/details/65445754
- https://blog.csdn.net/lemon_tree12138/article/details/50393548
- https://www.jianshu.com/p/4f3c8f134833
- https://blog.csdn.net/zxzxzx0119/article/details/80012812
- https://blog.csdn.net/buffoon1900/article/details/51330990