题目链接
分析
题目好长
其实也不是很长,我感觉按照原题的说法去理解这个题会比较好理解一些。
就是说,我先从树上找到一个点,然后一步一步的去覆盖这棵树,你只能覆盖点权比你小的点,问覆盖整棵树需要你的权值最小是多少。
首先先考虑我会去从哪个点开始,显然是先覆盖点权大的,因为它迟早都要被覆盖,如果现在不去覆盖,那再覆盖它,它的点权就会增加,所以肯定要先覆盖点权大的,进而可以知道,一个点如果有可能成为最大值,它的点权最多只会被+2,因为我要去覆盖它,首先覆盖它的半相邻点,再去覆盖它的相邻点,
如果它变大了,那我下一步就要把它覆盖掉,因此答案最多只可能是最大值+2。
接下来就是一个分类讨论了,假设最大值为(max),我们只要找(max-1)的点就行了,因为(max-2)的点最多也只会被搞成(max),如果所有的(max-1)的点都连在(max)上,那我搞完(max)就能在他们增加1到(max-1+1)的时候,破坏掉他们,所以此时答案为(max),如果一个(max-1)的点也没有,那答案显然也是这个。
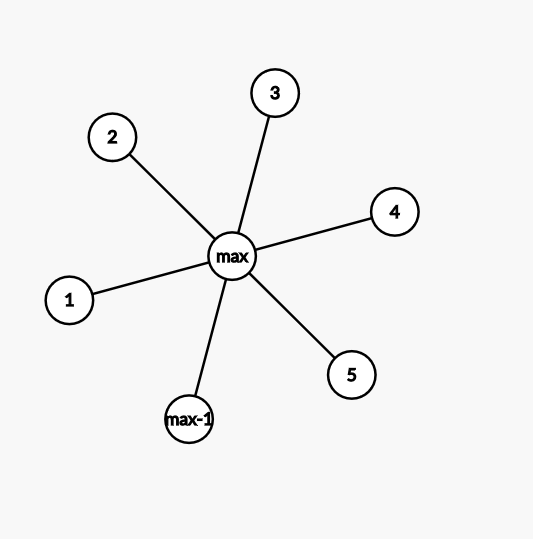
如果他们不连在一起呢?
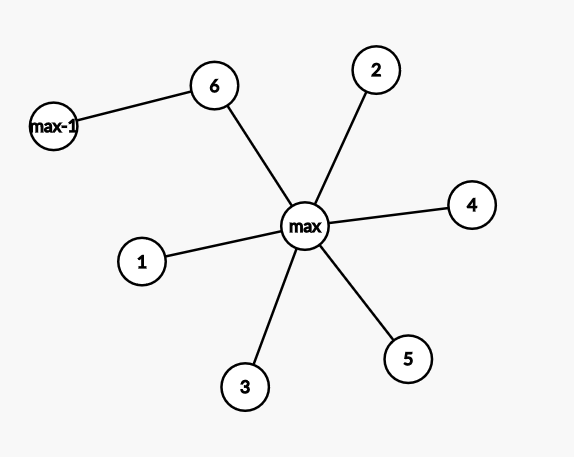
那我覆盖(max)和6的时候,(max-1)都要+1,最后就成了(max+1),所以当没有连在一起的时候,就是(max+1)。
那么有不止一个(max)的时候呢?
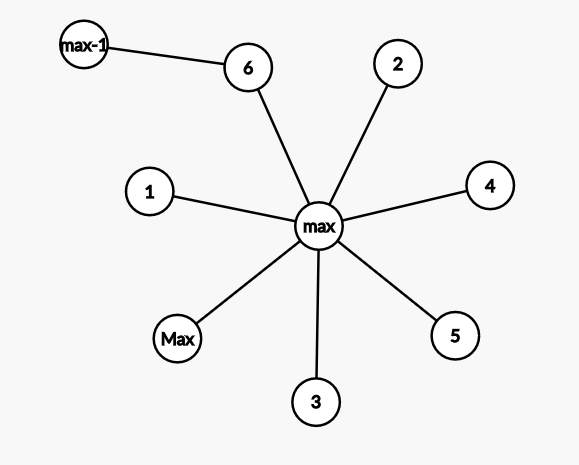
如果这些都连在一起,答案是(max+1),不管是连在(max)上还是别的上边,只要他们互为相邻点或半相邻点就好。
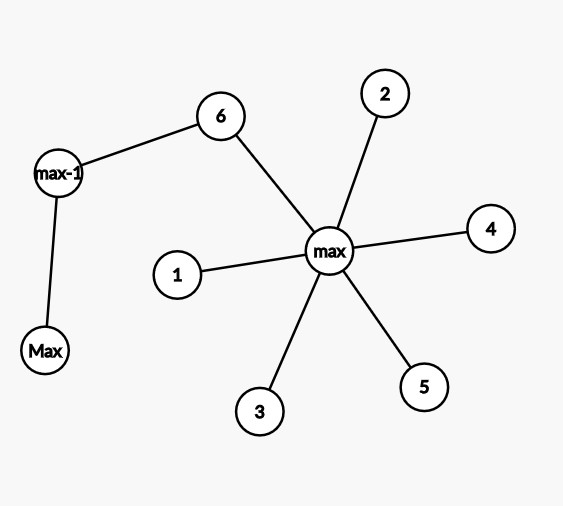
那么跟上边推(max-1)的时候一样,只不过(max)最多变成(max+2)。
也就这几种情况了,模拟一下就出来??
#include<cstdio>
#include<limits>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=3e5+10;
struct Edge{
int to,nxt;
}e[N<<1];
int h[N],idx,w[N];
void Ins(int a,int b){
e[idx].to=b;e[idx].nxt=h[a];h[a]=idx++;
}
int main(){
memset(h,-1,sizeof(h));
int n,mx,cnt,cntsec,pos;
mx=INT_MIN;cntsec=cnt=0;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&w[i]);
if(w[i]>mx){
mx=w[i];
pos=i;
}
}
for(int i=1;i<=n;i++){
if(w[i]==mx)cnt++;
if(w[i]==mx-1)cntsec++;
}
for(int i=1;i<n;i++){
int a,b;
scanf("%d%d",&a,&b);
Ins(a,b);
Ins(b,a);
}
if(cnt==1){
if(cntsec==0){
printf("%d
",mx);
return 0;
}
int nxt=0;
for(int i=h[pos];~i;i=e[i].nxt){
if(w[e[i].to]==mx-1)nxt++;
}
if(nxt==cntsec)
printf("%d
",mx);
else printf("%d
",mx+1);
return 0;
}
if(cnt>1){
for(int i=1;i<=n;i++){
int nxt=0;
for(int j=h[i];~j;j=e[j].nxt){
if(w[e[j].to]==mx)nxt++;
}
if((nxt==cnt&&w[i]!=mx)||(nxt==cnt-1&&w[i]==mx)){
printf("%d
",mx+1);
return 0;
}
}
}
printf("%d
",mx+2);
return 0;
}