【单调栈 动态规划】bzoj1057: [ZJOI2007]棋盘制作

好像还有个名字叫做“极大化”？

Description

　　国际象棋是世界上最古老的博弈游戏之一，和中国的围棋、象棋以及日本的将棋同享盛名。据说国际象棋起源

于易经的思想，棋盘是一个8*8大小的黑白相间的方阵，对应八八六十四卦，黑白对应阴阳。而我们的主人公小Q，

正是国际象棋的狂热爱好者。作为一个顶尖高手，他已不满足于普通的棋盘与规则，于是他跟他的好朋友小W决定

将棋盘扩大以适应他们的新规则。小Q找到了一张由N*M个正方形的格子组成的矩形纸片，每个格子被涂有黑白两种

颜色之一。小Q想在这种纸中裁减一部分作为新棋盘，当然，他希望这个棋盘尽可能的大。不过小Q还没有决定是找

一个正方形的棋盘还是一个矩形的棋盘（当然，不管哪种，棋盘必须都黑白相间，即相邻的格子不同色），所以他

希望可以找到最大的正方形棋盘面积和最大的矩形棋盘面积，从而决定哪个更好一些。于是小Q找到了即将参加全

国信息学竞赛的你，你能帮助他么？

Input

　　第一行包含两个整数N和M，分别表示矩形纸片的长和宽。接下来的N行包含一个N * M的01矩阵，表示这张矩形

纸片的颜色（0表示白色，1表示黑色）。

Output

　　包含两行，每行包含一个整数。第一行为可以找到的最大正方形棋盘的面积，第二行为可以找到的最大矩形棋

盘的面积（注意正方形和矩形是可以相交或者包含的）。

Sample Input

3 3
1 0 1
0 1 0
1 0 0

Sample Output

4
6

HINT

N, M ≤ 2000

---

题目分析

第一步先插空把数字取反，把“黑白相间”这个条件转为求最大0/1矩形。

如果只是求最大的正方形，用dp非常容易解决。但因为这里还要求最大矩形，所以用单调栈会更加方便一些。

先预处理$s[i][j]$表示在第$i$行，以第$j$列为结束的0序列长度。

处理出这个东西以后，先固定一列$j$，再枚举每一行$i$。对于这个枚举出来的点$(i,j)$，就可以利用预处理出的$s[i][j]$来寻找它向上所能最大扩张长度。

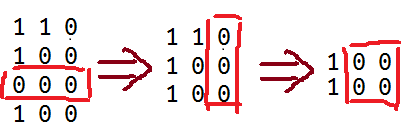
实际处理的过程如图所示。

另推荐一篇博客：https://blog.csdn.net/Tag_king/article/details/45166051

#include<bits/stdc++.h>
const int maxn = 2035;

struct node
{
    int x,h;
    node(int a=0, int b=0):x(a),h(b) {}
}stk[maxn];
int n,m,cnt;
int squ,rect;
int a[maxn][maxn],s[maxn][maxn];

int read()
{
    char ch = getchar();
    int num = 0;
    bool fl = 0;
    for (; !isdigit(ch); ch = getchar())
        if (ch=='-') fl = 1;
    for (; isdigit(ch); ch = getchar())
        num = (num<<1)+(num<<3)+ch-48;
    if (fl) num = -num;
    return num;
}
int sqr(int x){return x*x;}
void push(int x, int h)
{
    int now = x;
    while (cnt&&stk[cnt].h > h)
    {
        squ = std::max(squ, sqr(std::min(x-stk[cnt].x, stk[cnt].h)));
        rect = std::max(rect, (x-stk[cnt].x)*stk[cnt].h);
        now = stk[cnt].x;
        cnt--;
    }
    stk[++cnt] = node(now, h);
}
void calc()
{
    for (int i=1; i<=n; i++)
        for (int j=1; j<=m; j++)
            s[i][j] = a[i][j]?0:s[i][j-1]+1;
    for (int j=1; j<=m; j++)
    {
        cnt = 0;
        for (int i=1; i<=n; i++) push(i, s[i][j]);
        push(n+1, 0);
    }
}
int main()
{
    n = read(), m = read();
    for (int i=1; i<=n; i++)
        for (int j=1; j<=m; j++)
            (i+j)%2?a[i][j] = read():a[i][j] = 1-read();
    calc();
    for (int i=1; i<=n; i++)
        for (int j=1; j<=m; j++)
            a[i][j] = 1-a[i][j];
    calc();
    printf("%d
%d
",squ,rect);
    return 0;
}

END