【树链剖分 差分】bzoj3626: [LNOI2014]LCA

把LCA深度转化的那一步还是挺妙的。之后就是差分加大力数据结构了。

Description

给出一个n个节点的有根树（编号为0到n-1，根节点为0）。一个点的深度定义为这个节点到根的距离+1。
设dep[i]表示点i的深度，LCA(i,j)表示i与j的最近公共祖先。
有q次询问，每次询问给出l r z，求sigma_{l<=i<=r}dep[LCA(i,z)]。
（即，求在[l,r]区间内的每个节点i与z的最近公共祖先的深度之和）

Input

第一行2个整数n q。
接下来n-1行，分别表示点1到点n-1的父节点编号。
接下来q行，每行3个整数l r z。

Output

输出q行，每行表示一个询问的答案。每个答案对201314取模输出

Sample Input

5 2
0
0
1
1
1 4 3
1 4 2

Sample Output

8
5

HINT

共5组数据，n与q的规模分别为10000,20000,30000,40000,50000。

---

题目分析

我的做法&图片分析

由于树的标号是随便标的，所以这里的$[l,r]$区间操作在树上并没有什么大的特殊意义。

注意到如果$z$是给定的话，那么由于答案可减，我们可以对于序列来分块。

当然分块只是一种想法，再来挖掘一下$z$给定情况的性质。

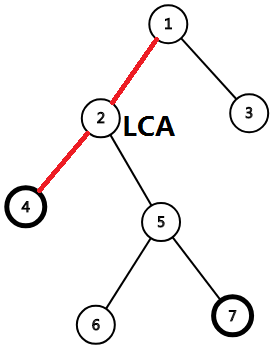
这里求4和7的LCA。自然，LCA就是两点到根节点的第一个公共节点。不过这幅图可能还没看出什么。

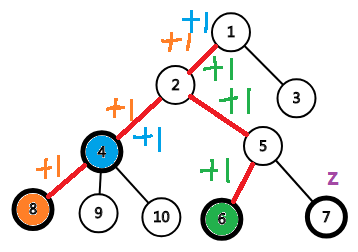
这幅图里7号节点是z，4,6,8节点是与z节点查询的节点。我们把与z节点查询的节点都沿路径向根方向+1。

这样只需要查询z节点到根节点的路径权值和就能算出所有LCA的深度之和了。

注意到这样处理之后，预处理的信息对于任意的z都适用了。

至于题目要求的“根节点深度为1”，正好可以让我们把边权化为点权，做起来也更加方便。

更理论化的题解

在黄学长博客上看到一篇更加严谨的题解：

显然，暴力求解的复杂度是无法承受的。
考虑这样的一种暴力，我们把 z 到根上的点全部打标记，对于 l 到 r 之间的点，向上搜索到第一个有标记的点求出它的深度统计答案。观察到，深度其实就是上面有几个已标记了的点（包括自身）。所以，我们不妨把 z 到根的路径上的点全部 +1，对于 l 到 r 之间的点询问他们到根路径上的点权和。仔细观察上面的暴力不难发现，实际上这个操作具有叠加性，且可逆。也就是说我们可以对于 l 到 r 之间的点 i，将 i 到根的路径上的点全部 +1, 转而询问 z 到根的路径上的点（包括自身）的权值和就是这个询问的答案。把询问差分下，也就是用 [1, r] − [1, l − 1] 来计算答案，那么现在我们就有一个明显的解法。从 0 到 n − 1 依次插入点 i，即将 i 到根的路径上的点全部+1。离线询问答案即可。我们现在需要一个数据结构来维护路径加和路径求和，显然树链剖分或LCT 均可以完成这个任务。树链剖分的复杂度为 O((n + q)· log n · log n)，LCT的复杂度为 O((n + q)· log n)，均可以完成任务。至此，题目已经被我们完美解决。

（大力数据结构~）

#include<bits/stdc++.h>
const int MO = 201314;
const int maxn = 50035;
const int maxm = 50035;

struct node
{
    int fa,top,son,tot;
}a[maxn];
struct QRs
{
    int x,id,opt;
    QRs(int a=0, int b=0, int c=0):x(a),id(b),opt(c) {}
    bool operator < (QRs a) const
    {
        return x < a.x;
    }
}q[maxn<<1];
int chain[maxn],chTot;
int f[maxn<<2],add[maxn<<2];
int edges[maxm],nxt[maxm],head[maxn],edgeTot;
int ansAdd[maxn],ansDel[maxn],qr[maxn];
int n,m,tot;

int read()
{
    char ch = getchar();
    int num = 0;
    bool fl = 0;
    for (; !isdigit(ch); ch = getchar())
        if (ch=='-') fl = 1;
    for (; isdigit(ch); ch = getchar())
        num = (num<<1)+(num<<3)+ch-48;
    if (fl) num = -num;
    return num;
}
void addedge(int u, int v)
{
    edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot;
}
void dfs1(int x, int fa)
{
    a[x].fa = fa, a[x].son = -1, a[x].tot = 1;
    for (int i=head[x]; i!=-1; i=nxt[i])
    {
        int v = edges[i];
        dfs1(v, x), a[x].tot += a[v].tot;
        if (a[x].son==-1||a[a[x].son].tot < a[v].tot)
            a[x].son = v;
    }
}
void dfs2(int x, int top)
{
    chain[x] = ++chTot, a[x].top = top;
    if (a[x].son==-1) return;
    dfs2(a[x].son, top);
    for (int i=head[x]; i!=-1; i=nxt[i])
        if (edges[i]!=a[x].son)
            dfs2(edges[i], edges[i]);
}
void pushup(int x)
{
    f[x] = (f[x<<1]+f[x<<1|1])%MO;
}
void pushdown(int x, int l, int r)
{
    if (add[x]){
        add[x<<1] += add[x], add[x<<1|1] += add[x];
        f[x<<1] += l*add[x], f[x<<1|1] += r*add[x];
        f[x<<1] %= MO, f[x<<1|1] %= MO;
        add[x] = 0;
    }
}
void update(int rt, int L, int R, int l, int r)
{
    if (L <= l&&r <= R){
        add[rt]++, f[rt] = (f[rt]+r-l+1)%MO;
        return;
    }
    int mid = (l+r)>>1;
    pushdown(rt, mid-l+1, r-mid);
    if (L <= mid) update(rt<<1, L, R, l, mid);
    if (R > mid) update(rt<<1|1, L, R, mid+1, r);
    pushup(rt);
}
void updateChain(int x, int y)
{
    while (a[x].top!=a[y].top)
    {
        update(1, chain[a[x].top], chain[x], 1, n);
        x = a[a[x].top].fa;
    }
    update(1, chain[y], chain[x], 1, n);
}
int query(int rt, int L, int R, int l, int r)
{
    if (L <= l&&r <= R) return f[rt];
    int mid = (l+r)>>1, ret = 0;
    pushdown(rt, mid-l+1, r-mid);
    if (L <= mid) ret += query(rt<<1, L, R, l, mid);
    if (R > mid) ret += query(rt<<1|1, L, R, mid+1, r);
    return ret%MO;
}
int queryChain(int x, int y)
{
    int ret = 0;
    while (a[x].top!=a[y].top)
    {
        ret += query(1, chain[a[x].top], chain[x], 1, n);
        x = a[a[x].top].fa;
    }
    ret += query(1, chain[y], chain[x], 1, n);
    return ret%MO;
}
int main()
{
    memset(head, -1, sizeof head);
    n = read(), m = read();
    for (int i=1; i<n; i++) addedge(read(), i);
    for (int i=1; i<=m; i++)
    {
        q[++tot] = QRs(read()-1, i, 0), q[++tot] = QRs(read(), i, 1);
        qr[i] = read();
    }
    std::sort(q+1, q+tot+1);
    dfs1(0, -1);
    dfs2(0, 0);
    int now = -1;
    for (int i=1; i<=tot; i++)
    {
        while (now < q[i].x)
            updateChain(++now, 0);
        int id = q[i].id;
        if (q[i].opt)
            ansAdd[id] = queryChain(qr[id], 0);
        else ansDel[id] = queryChain(qr[id], 0);
    }
    for (int i=1; i<=m; i++)
        printf("%d
",(ansAdd[i]-ansDel[i]+MO)%MO);
    return 0;
}

END