做到最后发现还是读题比赛;不过还是很好的图论题的
Description
一年一度的假面舞会又开始了,栋栋也兴致勃勃的参加了今年的舞会。今年的面具都是主办方特别定制的。每个参加舞会的人都可以在入场时选择一 个自己喜欢的面具。每个面具都有一个编号,主办方会把此编号告诉拿该面具的人。为了使舞会更有神秘感,主办方把面具分为k (k≥3)类,并使用特殊的技术将每个面具的编号标在了面具上,只有戴第i 类面具的人才能看到戴第i+1 类面具的人的编号,戴第k 类面具的人能看到戴第1 类面具的人的编号。 参加舞会的人并不知道有多少类面具,但是栋栋对此却特别好奇,他想自己算出有多少类面具,于是他开始在人群中收集信息。 栋栋收集的信息都是戴第几号面具的人看到了第几号面具的编号。如戴第2号面具的人看到了第5 号面具的编号。栋栋自己也会看到一些编号,他也会根据自己的面具编号把信息补充进去。由于并不是每个人都能记住自己所看到的全部编号,因此,栋栋收集的信 息不能保证其完整性。现在请你计算,按照栋栋目前得到的信息,至多和至少有多少类面具。由于主办方已经声明了k≥3,所以你必须将这条信息也考虑进去。
Input
第一行包含两个整数n, m,用一个空格分隔,n 表示主办方总共准备了多少个面具,m 表示栋栋收集了多少条信息。接下来m 行,每行为两个用空格分开的整数a, b,表示戴第a 号面具的人看到了第b 号面具的编号。相同的数对a, b 在输入文件中可能出现多次。
Output
包含两个数,第一个数为最大可能的面具类数,第二个数为最小可能的面具类数。如果无法将所有的面具分为至少3 类,使得这些信息都满足,则认为栋栋收集的信息有错误,输出两个-1。
Sample Input
6 5
1 2
2 3
3 4
4 1
3 5
【输入样例二】
3 3
1 2
2 1
2 3
Sample Output
4 4
【输出样例二】
-1 -1
HINT
100%的数据,满足n ≤ 100000, m ≤ 1000000。
题目分析
naive
首先会有一个很naive的想法:
对于无环的图找最大值:拓扑地从1开始标号dfs做下去,中途检查边$(u,v)$,若$v$已经被标号且$col_v≠col_u+1$,就是不合法的,随即输出"-1 -1"。
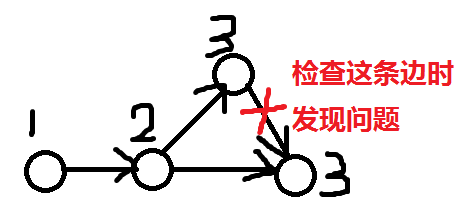
讲上去求的是最大值所以看上去很对劲是吧?
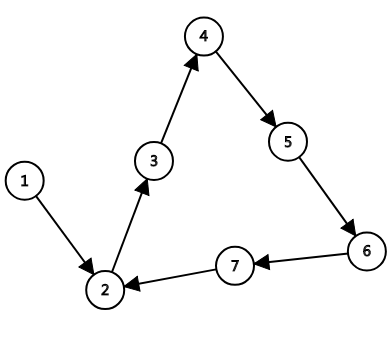
但是遇上这么一个环呢?7之后连的是2,所以判成无解。但是然而实际上$k=3$是成立的。
也就是说,简单地考虑“环缩点”或者“直接染色”是行不通的。
实际做法
学了tarjan之后不要在找环只想到tarjan!
这个问题其实建个反向边之后,可以分为两类:
- 有环的
- 没环的
没环的情况:树是很简单的,最大值就是所有树的最长链总和,最小值一定是3。
有环的情况:
DFS听上去很基础吧,但是切不要以为基础的东西就没什么用处。
这里依靠DFS找出每一个环的长度,并且注意到最大答案就是所有环长度的gcd。只要最终的$gcd≥3$,结合没环情况的下界可知环外其他树对答案不造成影响。
可能会想到环套环的情况。不过首先这个DFS要永久标记访问,复杂度是$O(n)$的,不会被卡;其次我们求的是环长度的gcd,并且如果答案合法,大环长度一定是小环的倍数,所以即便大环套在小环外,也不影响最终答案。
大致思路就是这样。
细节注意树的情况,最大值是所有树的最长链总和!
1 #include<bits/stdc++.h> 2 const int maxn = 100035; 3 const int maxm = 1000035; 4 5 struct node 6 { 7 int id; 8 std::vector<int> norEdge,difEdge; 9 }a[maxn]; 10 int n,m,cnt,mn,mx,chain,ans; 11 bool vis[maxn]; 12 std::pair<int, int> edges[maxm]; 13 14 int read() 15 { 16 char ch = getchar(); 17 int num = 0; 18 bool fl = 0; 19 for (; !isdigit(ch); ch = getchar()) 20 if (ch=='-') fl = 1; 21 for (; isdigit(ch); ch = getchar()) 22 num = (num<<1)+(num<<3)+ch-48; 23 if (fl) num = -num; 24 return num; 25 } 26 int gcd(int x, int y){return !y?x:gcd(y, x%y);} 27 void addedge(int x) 28 { 29 int u = edges[x].first, v = edges[x].second; 30 a[u].norEdge.push_back(v), a[v].difEdge.push_back(u); 31 } 32 void dfs(int x, int lb) 33 { 34 if (vis[x]){ 35 ans = gcd(ans, abs(a[x].id-lb)); //找到一个环了 36 return; 37 } 38 a[x].id = lb, vis[x] = 1; 39 mn = std::min(mn, lb), mx = std::max(mx, lb); 40 int sa = a[x].norEdge.size(), sb = a[x].difEdge.size(); 41 for (int i=0; i<sa; i++) 42 dfs(a[x].norEdge[i], lb+1); //正向边 43 for (int i=0; i<sb; i++) 44 dfs(a[x].difEdge[i], lb-1); //反向边 45 return; 46 } 47 int main() 48 { 49 // freopen("testdata.in","r",stdin); 50 n = read(), m = read(); 51 for (int i=1; i<=m; i++) 52 edges[i].first = read(), edges[i].second = read(); 53 std::sort(edges+1, edges+m+1); //用pair存边方便去重 54 addedge(1); 55 for (int i=2; i<=m; i++) 56 if (edges[i]!=edges[i-1]) 57 addedge(i); 58 for (int i=1; i<=n; i++) 59 if (!vis[i]){ //由于建了双向边,故不用考虑拓扑序 60 dfs(i, 0); 61 chain += mx-mn+1; 62 mn = mx = 0; 63 } 64 if (ans >= 3){ //如果有环并且合法 65 for (int i=3; i<=ans/2; i++) 66 if (ans%i==0){ 67 printf("%d %d ",ans,i); //找最小的答案——求最小约数 68 return 0; 69 } 70 printf("%d %d ",ans,ans); //最小答案还是ans 71 return 0; 72 } 73 if (!ans&&chain>=3){ 74 printf("%d %d ",chain,3); 75 return 0; 76 } //否则不合法,ans=1 77 printf("-1 -1 "); 78 return 0; 79 }
END