【计数】7.11跳棋

很好的题

题目描述

小A是跳棋大师。跳棋的规则是，一颗棋子可以移动一个单位，或者移动越过一个另一个棋子运动一个单位。小A在一条数轴上放了n颗棋子，第i颗棋子位于aiai的位置，然后给了每个棋子一个编号。现在小A想要知道，所有跳棋到达0的可能顺序有多少种。出于某些模因污染，小A只会向左移动跳棋。

输入格式

第一行一个整数nn接下来一行nn个整数描述aiai保证ai<ai+1ai<ai+1

输出格式

一个整数，表示可能的方案数,mod 1000000007后输出

样例输入

3

1 2 3

样例输出

4

样例解释

3不能同时越过1和2，所以可行的顺序有123,132,231,213

数据规模与约定

对于30%的数据，满足n≤8n≤8对于60%的数据，满足ai>=ai+1−2ai>=ai+1−2另存在10%数据满足ai=iai=i对于100%的数据，满足n≤1000000,0<ai<=109

---

题目分析

我的分析

初看这题觉得无从下手，连暴力都写不来。

不过可以明确的是肯定会想到把棋子离散化，可是这里又不能够直接全部离散化。因为如果把原先分离的一大堆棋子离散化成堆在一起的棋子，那么有些棋子就不能够向前跳了。

具体考虑一下什么情况下才能够离散化；并且应该离散化成什么样子。

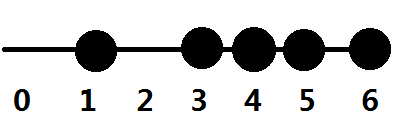
比如说有这样一组棋子，那么第一个走到终点的只能是1或3或4。但是如果间距变为3，所有棋子就都能变为第一个走到终点的棋子了。

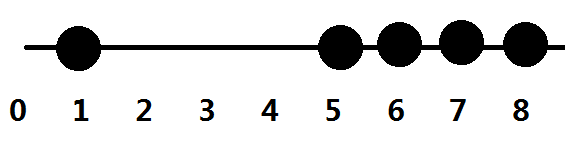
看上去好像毫无规律，那再换一个方式看间距为3的情况。

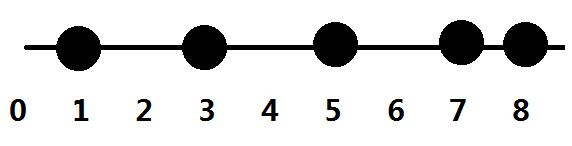
这两种情况之所以等价，是因为题目要求的是棋子跳到终点的顺序，而非跳到终点前的状态。

那么也就是说，在使得尽可能多的棋子能够作为第一个跳到终点的情况下，相邻两个棋子最多只需间隔为1就可以了。

    for (int i=1; i<=n; i++)
        a[i] = std::min(a[i], a[i-1]+2);

于是可以将距离作如上处理。

但是这样处理之后，还会像最初一样，有棋子紧挨着另一个的情况出现。

关键好处就在于，我们这般处理了距离后，剩下紧挨着的棋子必定是会堵住后方棋子的去路的。

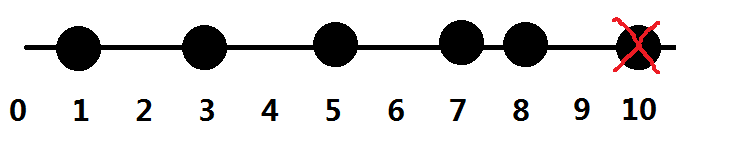
就拿上面那张图来说，由于题目要求棋子不能向右移动，所以无论如何10这个棋子都是不能第一个到达的。因此第一个移动棋子总共有5种方案。

接下去的步骤似乎看上去就变麻烦了，因为只有选择移动了8才能继续移动10————是这样吗？

注意到所有棋子其实都是一样的。看上去是句废话，但是这意味着，无论第一次移动前5个棋子中的哪个，之后的局面都可以看作是移走了最后这个挡住其他棋子的棋子。

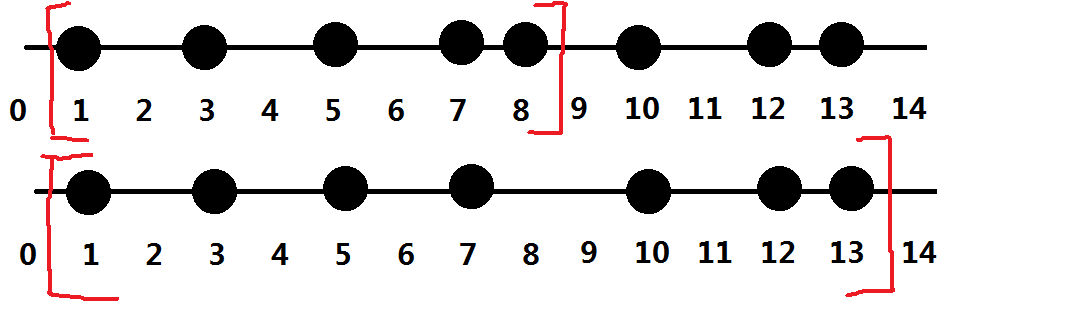
局面本质上就是这样变化的，因为第八颗棋子总是能够“找到理由”跳到被移走的那个位置上。

明确了这个又有什么作用呢？这个特性使得我们可以一边处理那些“挡路”的棋子，一边计算这些“挡路”棋子对于答案的贡献。否则若对于整个区间来考虑“挡路”棋子的贡献和对后面布局的影响，会是很麻烦的事情。

    for (int i=1; i<=n; i++)
    {
        a[i] = std::min(a[i], a[i-1]+2);
        if (a[i]==a[i-1]+1){
            a[i] = a[i-1];
            ans = 1ll*ans*(i+tot-n)%MO;
            tot--;
        }
    }

最后剩下的棋子必定是这样的：

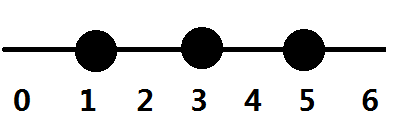
代码（典型的代码复杂度与思维复杂度成反比:(）

#include<bits/stdc++.h>
typedef long long ll;
const ll MO = 1e9+7;
const int maxn = 1000035;

int n,tot,ans;
int a[maxn]; 

int main()
{
    freopen("chess.in","r",stdin);
    freopen("chess.out","w",stdout);
    scanf("%d",&n);
    tot = n, ans = 1, a[0] = -1;
    for (int i=1; i<=n; i++) scanf("%d",&a[i]);
    for (int i=1; i<=n; i++)
    {
        a[i] = std::min(a[i], a[i-1]+2);
        if (a[i]==a[i-1]+1){
            a[i] = a[i-1];
            ans = 1ll*ans*(i+tot-n)%MO;
            tot--;
        }
    }
    for (int i=1; i<=tot; i++)
        ans = 1ll*ans*i%MO;
    printf("%d
",ans); 
    return 0;
}

官方题解

考虑一个比较简单的情况：1、3、5、7、9...这种时候答案显然是n!n!因为我们可以让任意一个棋子在其他棋子不移动的情况下成为下一个到达的棋子。也不难证明这是最“劣”的能够有n!n!种方案的情况。棋子与棋子除了编号并没有不同，换而言之一个棋子离开之后后面的棋子如果能够到达他的位置就可以顶替他。首先把所有棋子都尽可能向左靠，因为越向左靠对后面的棋子来说有更多的调整空间。比如1 5 6 7，往左靠就可以得到1 3 5 7的情况。当某个位置不得不出现相邻两颗棋子距离为1的情况时，比如1、3、4，此时能够作为下一个到达的棋子就只有前面三颗，因为后面的棋子不能同时越过相邻的两颗。然后考虑一颗棋子离开了会怎样，无论是哪颗棋子离开了，第三颗都可以到达他的位置，无论是谁离开，最后都可以到达1、3这个“较优”的状态。所以这样模拟一遍就好了。注意最后的边界状况。

END