解方程题!
Description
Bessie学会了刺绣这种精细的工作。牛们在一片半径为d(1 <= d <= 50000)的圆形布上绣花. 它们一共绣了N (2 <= N <= 50000)条直线,每条直线连接布的边缘上的两个点(没有两条线通过边上同一个点)。 作为一只热爱数学的牛,Bessie 知道每条线的公式, ax + by + c = 0. a, b, 和 c 为整数(-1000000 <= a <= 1000000; -1000000 <= b <= 1000000; -1000000 <= c <= 1000000).没有两条线完全重合。 不幸的是, 一部分线不通过圆布的内部. 原点(0,0)在布的正中央, 所有边上的点离原点距离为d. 每条线的公式满足至少a,b中的一个非零. 对于牛来说,刺绣作品中线的交点越多,便越有价值。帮助Bessie计算在圆中相交的线的对数,也就是说交点与原点的距离小于d。注意如果三条线在圆内同一点相交,这算3对线。4线共点->6对线.
Input
第1行: 两个空格分开的数, N 和 d 第2..N+1行: 第 i+1 行包含第i条线的参数: a, b 和 c
Output
第1行: 一行,包含一个数,为在园内相交的线的对数.
Sample Input
1 0 0
0 1 0
输入说明:
两条直线x=0和y=0.
Sample Output
HINT
两条线在(0,0)相交, 明显离原点距离小于1.
题目分析
模型转化
$n=50000$的数据规模,$n^2$的枚举肯定不行。那么可以省去哪些枚举呢?
先考虑哪些线段才会相交。
因为对于一条直线,有效部分就只有与圆内的公共部分。所以我们只需要记录直线与圆的两个交点。
但是由于会出现如下图所示情况,
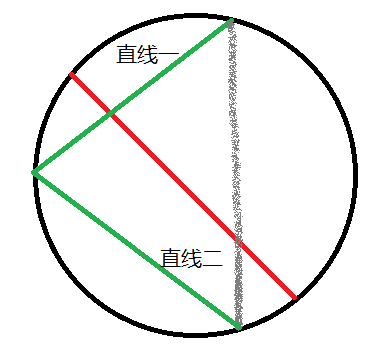
还需要把x轴坐标再映射一下。若$y<0$,则$L=-x-r$;反之$R=x+r$。
自然发现这样映射之后,圆上任意一点都有了唯一的映射值。
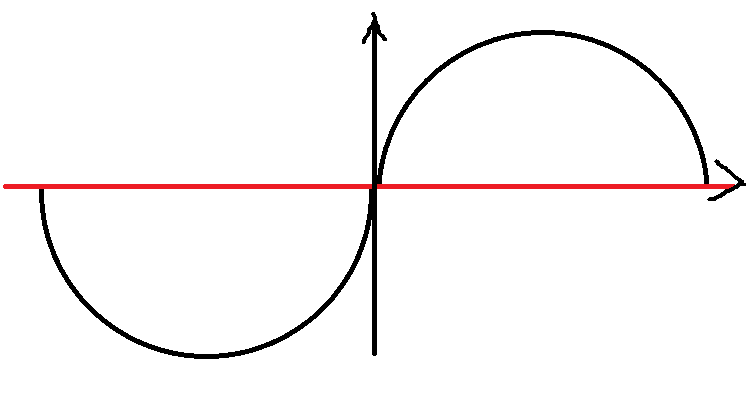
实际上就是变成了这样。
于是直线在圆内相交就等价于映射后的线段下相交(不包含)。
树状数组维护
如何处理相交但不包含的线段条数?
这里有一种挺妙的方法:先把线段按照左端点排序,这样保证了处理时左端点的有序。然后计算线段内的右端点个数。因为之前处理的线段左端点都是小于等于现在处理的左端点的,所以线段内的右端点个数就是与现在处理的线段的相交的线段条数。
这样子就可以离散化后用树状数组做了。
(树状数组好棒啊!)
1 #include<bits/stdc++.h> 2 const int maxn = 50005; 3 4 int n,d,cnt; 5 long long f[maxn<<1],ans; 6 double t[maxn<<1],xa,xb,ya,yb,a,b,c; 7 std::pair<double, double> mp[maxn]; 8 9 int read() 10 { 11 char ch = getchar(); 12 int num = 0; 13 bool fl = 0; 14 for (; !isdigit(ch); ch = getchar()) 15 if (ch=='-') fl = 1; 16 for (; isdigit(ch); ch = getchar()) 17 num = (num<<1)+(num<<3)+ch-48; 18 if (fl) num = -num; 19 return num; 20 } 21 int lowbit(int x){return x&-x;} 22 void add(int x){for (; x<maxn<<1; x+=lowbit(x)) f[x]++;} 23 int query(int x) 24 { 25 int ret = 0; 26 for (; x; x-=lowbit(x)) ret += f[x]; 27 return ret; 28 } 29 double calc(double x, double y){return y < 0?-x-d:x+d;} 30 int main() 31 { 32 n = read(), d = read(); 33 for (int i=1; i<=n; i++) 34 { 35 // int a = read(), b = read(), c = read(); 36 scanf("%lf%lf%lf",&a,&b,&c); 37 bool cte = 0; 38 xa = xb = ya = yb = 0; 39 if (!a || !b){ 40 if (!a){ 41 double h = -c/b; 42 if (h*h-d*d > 0) cte = 1; 43 else{ 44 xa = -sqrt(d*d*1.0-h*h), xb = -xa; 45 ya = yb = h; 46 } 47 }else{ 48 double w = -c/a; 49 if (w*w-d*d > 0) cte = 1; 50 else{ 51 xa = xb = w; 52 ya = sqrt(d*d*1.0-w*w), yb = -ya; 53 } 54 } 55 }else{ 56 double equa = a*a+b*b*1.0, equb = 2*a*c*1.0, equc = c*c*1.0-b*b*d*d*1.0; 57 double delta = equb*equb*1.0-4.0*equa*equc; 58 if (delta < 0) cte = 1; 59 else{ 60 xa = (-equb-sqrt(delta))/(2.0*equa); 61 xb = (-equb+sqrt(delta))/(2.0*equa); 62 ya = -(a*xa+c)/b; 63 yb = -(a*xb+c)/b; 64 } 65 } 66 if (cte) continue; 67 double L = calc(xa, ya), R = calc(xb, yb); 68 if (L > R) std::swap(L, R); 69 mp[++cnt] = std::make_pair(L, R); 70 t[cnt*2-1] = L, t[cnt*2] = R; 71 } 72 std::sort(mp+1, mp+cnt+1); 73 std::sort(t+1, t+2*cnt+1); 74 for (int i=1; i<=cnt; i++) 75 { 76 int x = std::lower_bound(t+1, t+2*cnt+1, mp[i].first)-t; 77 int y = std::lower_bound(t+1, t+2*cnt+1, mp[i].second)-t; 78 ans += query(y)-query(x-1); 79 add(y); 80 } 81 printf("%lld ",ans); 82 return 0; 83 }
END