tarjan缩点：口胡过好多题，不过从来没写过……
什么是缩点
tarjan和Kosaraju、Gabow算法一样，是为了求有向图中的强连通分量。因为有向图中大多数情况下会有环存在，而有环是一个不甚好的性质。如果把有向图里的所有强连通分量都看作是一个点（缩点），则原图就会变成一个DAG——DAG是一个好东西。
什么是tarjan缩点
tarjan算法网上大多有介绍，我也在之前看过多次，不过从未写过，这里不再介绍。
今天把核心代码重新看了一遍，终于深入理解了其算法。那么就不妨在这里直接放上代码。
tarjan代码
1 void tarjan(int now) 2 { 3 dfn[now] = low[now] = ++tim; //常规的dfn[]和low[] 4 stk[++cnt] = now; 5 for (int i=head[now]; i!=-1; i=nxt[i]) 6 { 7 int v = edges[i]; 8 if (!dfn[v]){ 9 tarjan(v); 10 low[now] = std::min(low[now], low[v]); 11 }else if (!col[v]) 12 low[now] = std::min(low[now], dfn[v]); //注意这里是dfn[v] 13 } 14 if (low[now]==dfn[now]) //最后的统计部分 15 { 16 col[now] = ++cols; 17 for (; stk[cnt]!=now; cnt--) 18 col[stk[cnt]] = cols; 19 cnt--; 20 } 21 }
用途
1.有向图的缩点
2.解决2-SAT
几道例题
【tarjan+DAGdp】P3387 【模板】缩点
题目背景
缩点+DP
题目描述
给定一个n个点m条边有向图，每个点有一个权值，求一条路径，使路径经过的点权值之和最大。你只需要求出这个权值和。
允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。
输入输出格式
输入格式：
第一行，n,m
第二行，n个整数，依次代表点权
第三至m+2行，每行两个整数u,v，表示u->v有一条有向边
输出格式：
共一行，最大的点权之和。
说明
n<=10^4,m<=10^5,点权<=1000
算法：Tarjan缩点+DAGdp
题目分析
嘛……具体算法在题面里都给出来了。缩点+dp。
我做法是缩完点后重新建边，长是长了点，不过要是到了其他题的话可移植性会大一些。
至于dp，只需要建一个超级源，然后从超级源开始记忆化搜索就好了。
1 #include<bits/stdc++.h> 2 const int maxn = 10005; 3 const int maxm = 100035; 4 5 int n,m; 6 int f[maxn],val[maxn],col[maxn],cols; 7 int edgeTot,edges[maxm],nxt[maxm],head[maxn]; 8 bool vis[maxn]; 9 10 int read() 11 { 12 char ch = getchar(); 13 int num = 0; 14 bool fl = 0; 15 for (; !isdigit(ch); ch = getchar()) 16 if (ch=='-') fl = 1; 17 for (; isdigit(ch); ch = getchar()) 18 num = (num<<1)+(num<<3)+ch-48; 19 if (fl) num = -num; 20 return num; 21 } 22 namespace tarjanSpace 23 { 24 int stk[maxn],cnt; 25 int a[maxn],dfn[maxn],low[maxn],tim; 26 int edgeTot,edges[maxm],nxt[maxm],head[maxn]; 27 void tarjan(int now) 28 { 29 dfn[now] = low[now] = ++tim; 30 stk[++cnt] = now; 31 for (int i=head[now]; i!=-1; i=nxt[i]) 32 { 33 int v = edges[i]; 34 if (!dfn[v]){ 35 tarjan(v); 36 low[now] = std::min(low[now], low[v]); 37 }else if (!col[v]) 38 low[now] = std::min(low[now], dfn[v]); 39 } 40 if (low[now]==dfn[now]) 41 { 42 ::col[now] = ++::cols; 43 for (; stk[cnt]!=now; cnt--) 44 ::col[stk[cnt]] = ::cols; 45 cnt--; 46 } 47 } 48 inline void addedgeInner(int u, int v) 49 { 50 edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot; 51 } 52 inline void addedgeOuter(int u, int v) 53 { 54 ::edges[++::edgeTot] = v, ::nxt[::edgeTot] = ::head[u], ::head[u] = ::edgeTot; 55 } 56 void dealOuter() 57 { 58 for (int i=1; i<=n; i++) ::val[::col[i]] += a[i]; 59 for (int i=1; i<=n; i++) 60 { 61 int u = col[i]; 62 for (int j=head[i]; j!=-1; j=nxt[j]) 63 { 64 int v = col[edges[j]]; 65 addedgeOuter(u, v); 66 } 67 } 68 for (int i=1; i<cols; i++) addedgeOuter(0, i); 69 } 70 void solve() 71 { 72 memset(head, -1, sizeof head); 73 n = read(), m = read(), cnt = tim = edgeTot = 0; 74 for (int i=1; i<=n; i++) a[i] = read(), addedgeInner(0, i); 75 for (int i=1; i<=m; i++) 76 { 77 int u = read(), v = read(); 78 addedgeInner(u, v); 79 } 80 tarjan(0); 81 dealOuter(); 82 } 83 } 84 void dp(int now) 85 { 86 if (vis[now]) return; 87 vis[now] = 1; 88 for (int i=head[now]; i!=-1; i=nxt[i]) 89 { 90 int v = edges[i]; 91 dp(v); 92 f[now] = std::max(f[now], f[v]); 93 } 94 f[now] += val[now]; 95 } 96 int main() 97 { 98 memset(head, -1, sizeof head); 99 tarjanSpace::solve(); 100 dp(0); 101 printf("%d ",f[0]); 102 return 0; 103 }
【tarjan】bzoj1051: [HAOI2006]受欢迎的牛
Description
每一头牛的愿望就是变成一头最受欢迎的牛。现在有N头牛，给你M对整数(A,B)，表示牛A认为牛B受欢迎。 这
种关系是具有传递性的，如果A认为B受欢迎，B认为C受欢迎，那么牛A也认为牛C受欢迎。你的任务是求出有多少头
牛被所有的牛认为是受欢迎的。
Input
第一行两个数N,M。 接下来M行，每行两个数A,B，意思是A认为B是受欢迎的（给出的信息有可能重复，即有可
能出现多个A,B）
Output
一个数，即有多少头牛被所有的牛认为是受欢迎的。
Sample Input
3 3
1 2
2 1
2 3
1 2
2 1
2 3
Sample Output
1
HINT
100%的数据N<=10000,M<=50000
题目分析
一个最基础的方法就是把每只奶牛都开一个认可数组vis[]并且赋一个标号，对于出边传递自己所有的认可，这样子到最后统计有多少牛拥有所有认可就好了。
那么为了避免死循环是要先拓扑排序一遍的，但是这张图如果存在环呢？存在环就不能只这样操作了。
当做法因为环的存在而不适用的时候，自然就考虑到了缩点。
对于缩完点的图，我们再来观察一下：
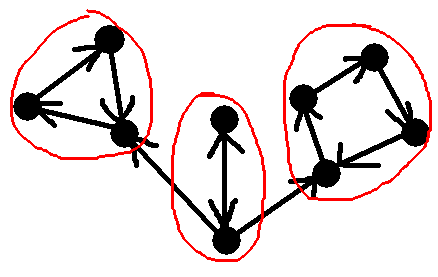
可以发现，这个DAG新图若存在强连通分量满足条件，则这个强连通分量一定是出度为零的。
这里不能够用入度是否为n-1判断，因为认可能够被传递，与入度没有直接关系。
还有非常重要的一点！如果建了超级源来联通森林，那么$maxm'=maxn+maxm$，不然要RE的！
1 #include<bits/stdc++.h> 2 const int maxn = 10035; 3 const int maxm = 60035; 4 5 int n,m; 6 int deg[maxn],stk[maxn],cnt; 7 int col[maxn],cols; 8 int dfn[maxn],low[maxn],size[maxn],tim; 9 int edgeTot,edges[maxm],nxt[maxm],head[maxn]; 10 11 int read() 12 { 13 char ch = getchar(); 14 int num = 0; 15 bool fl = 0; 16 for (; !isdigit(ch); ch = getchar()) 17 if (ch=='-') fl = 1; 18 for (; isdigit(ch); ch = getchar()) 19 num = (num<<1)+(num<<3)+ch-48; 20 if (fl) num = -num; 21 return num; 22 } 23 void addedge(int u, int v) 24 { 25 edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot; 26 } 27 void tarjan(int x) 28 { 29 dfn[x] = low[x] = ++tim; 30 stk[++cnt] = x; 31 for (int i=head[x]; i!=-1; i=nxt[i]) 32 { 33 int v = edges[i]; 34 if (!dfn[v]) 35 tarjan(v), low[x] = std::min(low[x], low[v]); 36 else if (!col[v]) 37 low[x] = std::min(low[x], dfn[v]); 38 } 39 if (dfn[x]==low[x]) 40 { 41 col[x] = ++cols, size[cols] = 1; 42 for (; stk[cnt]!=x; cnt--, size[cols]++) 43 col[stk[cnt]] = cols; 44 cnt--; 45 } 46 } 47 int main() 48 { 49 memset(head, -1, sizeof head); 50 n = read(), m = read(); 51 for (int i=1; i<=m; i++) 52 { 53 int u = read(), v = read(); 54 addedge(u, v); 55 } 56 for (int i=1; i<=n; i++) addedge(0, i); 57 tarjan(0); 58 for (int i=1; i<=n; i++) 59 for (int j=head[i]; j!=-1; j=nxt[j]) 60 if (col[i]!=col[edges[j]]) 61 deg[col[i]]++; 62 int tot = 0, gr = 0; 63 for (int i=1; i<cols; i++) 64 if (!deg[i]) 65 tot = size[i], gr++; 66 printf("%d ",gr>1?0:tot); 67 return 0; 68 }
【tarjan+拓扑排序】P1262 间谍网络
题目描述
由于外国间谍的大量渗入，国家安全正处于高度的危机之中。如果A间谍手中掌握着关于B间谍的犯罪证据，则称A可以揭发B。有些间谍收受贿赂，只要给他们一定数量的美元，他们就愿意交出手中掌握的全部情报。所以，如果我们能够收买一些间谍的话，我们就可能控制间谍网中的每一分子。因为一旦我们逮捕了一个间谍，他手中掌握的情报都将归我们所有，这样就有可能逮捕新的间谍，掌握新的情报。
我们的反间谍机关提供了一份资料，色括所有已知的受贿的间谍，以及他们愿意收受的具体数额。同时我们还知道哪些间谍手中具体掌握了哪些间谍的资料。假设总共有n个间谍(n不超过3000)，每个间谍分别用1到3000的整数来标识。
请根据这份资料，判断我们是否有可能控制全部的间谍，如果可以，求出我们所需要支付的最少资金。否则，输出不能被控制的一个间谍。
输入输出格式
输入格式：
第一行只有一个整数n。
第二行是整数p。表示愿意被收买的人数，1≤p≤n。
接下来的p行，每行有两个整数，第一个数是一个愿意被收买的间谍的编号，第二个数表示他将会被收买的数额。这个数额不超过20000。
紧跟着一行只有一个整数r，1≤r≤8000。然后r行，每行两个正整数，表示数对(A, B)，A间谍掌握B间谍的证据。
输出格式：
如果可以控制所有间谍，第一行输出YES，并在第二行输出所需要支付的贿金最小值。否则输出NO，并在第二行输出不能控制的间谍中，编号最小的间谍编号。
题目分析
这题显然我们首先要环缩点，然后对于DAG拓扑排序，所有入度为0的点都必须要选。
要注意一点的就是：若一个连通块是可控制的，它的代价是块内所有可贿赂间谍的最小值。
1 #include<bits/stdc++.h> 2 const int maxn = 3003; 3 const int maxm = 10003; 4 5 struct node 6 { 7 int id,val; 8 }a[maxn]; 9 int n,p,r,ans; 10 int low[maxn],dfn[maxn],tim; 11 int col[maxn],cols; 12 int stk[maxn],deg[maxn],val[maxn],cnt; 13 int edgeTot,edges[maxm],nxt[maxm],head[maxn]; 14 bool mp[maxn]; 15 16 int read() 17 { 18 char ch = getchar(); 19 int num = 0; 20 bool fl = 0; 21 for (; !isdigit(ch); ch = getchar()) 22 if (ch=='-') fl = 1; 23 for (; isdigit(ch); ch = getchar()) 24 num = (num<<1)+(num<<3)+ch-48; 25 if (fl) num = -num; 26 return num; 27 } 28 void addedge(int u, int v) 29 { 30 edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot; 31 } 32 void tarjan(int now) 33 { 34 dfn[now] = low[now] = ++tim; 35 stk[++cnt] = now; 36 for (int i=head[now]; i!=-1; i=nxt[i]) 37 { 38 int v = edges[i]; 39 if (!dfn[v]) 40 tarjan(v), 41 low[now] = std::min(low[now], low[v]); 42 else if (!col[v]) 43 low[now] = std::min(low[now], dfn[v]); 44 } 45 if (dfn[now]==low[now]) 46 { 47 col[now] = ++cols; 48 for (; stk[cnt]!=now; cnt--) 49 col[stk[cnt]] = cols; 50 cnt--; 51 } 52 } 53 int main() 54 { 55 memset(head, -1, sizeof head); 56 memset(val, 0x3f3f3f3f, sizeof val); 57 n = read(), p = read(); 58 for (int i=1; i<=p; i++) 59 a[i].id = read(), a[i].val = read(); 60 r = read(); 61 for (int i=1; i<=r; i++) 62 { 63 int u = read(), v = read(); 64 addedge(u, v); 65 } 66 for (int i=1; i<=n; i++) addedge(0, i); 67 tarjan(0); 68 for (int i=1; i<=p; i++) 69 { 70 int u = col[a[i].id]; 71 mp[u] = 1, val[u] = std::min(val[u], a[i].val); 72 } 73 for (int i=1; i<=n; i++) 74 for (int j=head[i]; j!=-1; j=nxt[j]) 75 if (col[i]!=col[edges[j]]) 76 deg[col[edges[j]]]++; 77 bool fl = 1; 78 // for (int i=1; i<cols&&fl; i++) 79 // if (!deg[i]&&!mp[col[a[i].id]]) 80 // fl = 0, ans = i; 81 // else ans += a[i].val; 82 // for (int i=1; i<=p; i++) 83 // if (!deg[col[a[i].id]]) 84 // ans += a[i].val; 85 for (int i=1; i<cols; i++) 86 if (mp[i]&&!deg[i]) ans += val[i]; 87 for (int i=1; i<=n&&fl; i++) 88 if (!deg[col[i]]&&!mp[col[i]]) 89 fl = 0, ans = i; 90 printf("%s %d ",fl?"YES":"NO",ans); 91 return 0; 92 }
END