区间DP
题目描述
丁丁最近沉迷于一个数字游戏之中。这个游戏看似简单，但丁丁在研究了许多天之后却发觉原来在简单的规则下想要赢得这个游戏并不那么容易。游戏是这样的，在你面前有一圈整数（一共n个），你要按顺序将其分为m个部分，各部分内的数字相加，相加所得的m个结果对10取模后再相乘，最终得到一个数k。游戏的要求是使你所得的k最大或者最小。
例如，对于下面这圈数字（n=4，m=2）：
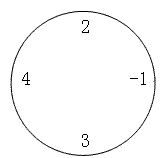
要求最小值时，((2-1) mod 10)×((4+3) mod 10)=1×7=7，要求最大值时，为((2+4+3) mod 10)×(-1 mod 10)=9×9=81。特别值得注意的是，无论是负数还是正数，对10取模的结果均为非负值。
丁丁请你编写程序帮他赢得这个游戏。
输入输出格式
输入格式：
输入文件第一行有两个整数，n（1≤n≤50）和m（1≤m≤9）。以下n行每行有个整数，其绝对值不大于104，按顺序给出圈中的数字，首尾相接。
输出格式：
输出文件有两行，各包含一个非负整数。第一行是你程序得到的最小值，第二行是最大值。
自己不好好玩游戏还要叫人帮忙写程序
大体思路就这样，展开成2n的链再区间内DP。转移方程是f[i][j][m] = max(f[i][j-1][m-1]*s[j][j], f[i][k][m-1]*s[k+1][j])，最小值同理。
那么时间复杂度是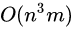
，还是可以接受的。实测洛谷5个点60ms。
不过这题呢坑点如下：
1.这个取模很有趣
2.最小值的g数组初始化有点意思。虽然数据范围不大，但是如果极端情况n=50,m=9,{ai}=104的话也是会出事的。好在数据非常人性，于是我用着奇奇怪怪的判别方法硬是初始化了过去。
这么快都2018年的寒假了，一年前这个时候都快开学了吧……
寒假切的第一题祭。
（怎么感觉这题都做了这么久……）