最短路径树上分层dp的一类套路吧
题目大意
幽香这几天学习了魔法,准备建造一个大型的时空传送阵。
幽香现在可以在幻想乡的n个地点建造一些传送门,如果她建造了从地点a与地点b之间的传送门,那么从a到b和从b到a都只需要单位1的时间。
同时这些地点之间在地理上是非常遥远的,因此来往他们必须使用传送门。
现在幽香想要问你,有多少种建造传送门的方案,使得地点1和地点n之间的最短距离恰好为k?两个方案不同当且仅当建造的传送门的集合不同。不能建造节点到自身的传送门,两个点之间也最多造一个传送门。
$n,k le 100$
题目分析
特殊性质在于每条边长度都为1,这点让人联想到bfs;而看到最短路则自然想起最短路径树。
那么我们就考虑按照bfs序dp这张图的最短路径树,也就是分层往下dp。在分层dp的树中,跨层的点不能连边;邻层及同层的点可以随意连边,最终目标是把$n$号点安排在$k+1$层,如果还有剩下的点则接下去随意安排。
不过这里有一种省去分类讨论的小trick:我们不计标号地计算剩下$n-1$个点的方案数,而由于这$n-1$个点是完全等价的,相当于最后再把总方案数乘以$(n-1)^{-1}$即可。
用$f_{i,t,l}$表示构造了$i$层,总共使用了$t$个节点(包括1号点),当前层有$l$个节点的方案数。转移时枚举上一层有$p$个节点。边界条件$f_{1,1,1}=1$
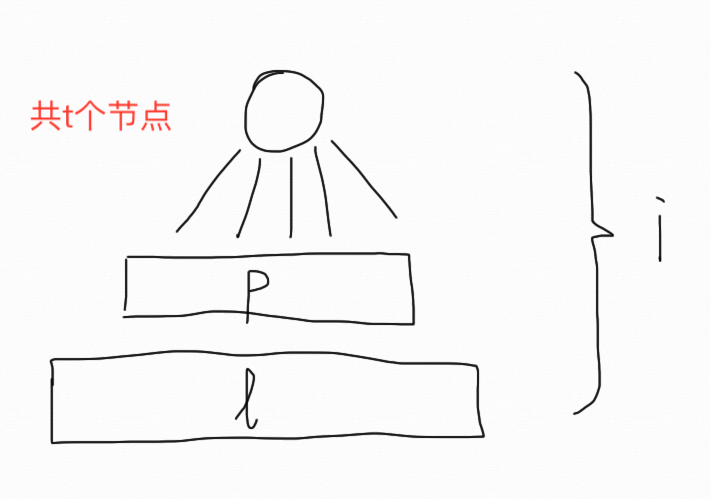
大致形状如上所示。
考虑p到l的转移:首先从$n-(t-l)$个点中取出$l$个点,取出的每个点向$p$个点连边有$2^p-1$种方案;$l$个点同层连边有$2^{lchoose 2}$种方案。
最后再枚举所有情况统计一趟即可。
1 #include<bits/stdc++.h> 2 #define MO 1000000007 3 typedef long long ll; 4 const int maxn = 103; 5 6 int n,k,fac[maxn],facinv[maxn],mi[maxn]; 7 ll f[maxn][maxn][maxn],ans; 8 9 int qmi(ll a, ll b) 10 { 11 int ret = 1; 12 for (a%=MO; b; b>>=1,a=1ll*a*a%MO) 13 if (b&1) ret = 1ll*ret*a%MO; 14 return ret; 15 } 16 int C(int n, int m) 17 { 18 if (n < m) return 0; 19 return 1ll*fac[n]*facinv[n-m]%MO*facinv[m]%MO; 20 } 21 int main() 22 { 23 scanf("%d%d",&n,&k); 24 facinv[0] = facinv[1] = fac[0] = mi[0] = 1; 25 for (int i=2; i<=100; i++) 26 facinv[i] = MO-1ll*MO/i*facinv[MO%i]%MO; 27 for (int i=1; i<=100; i++) 28 mi[i] = 2ll*mi[i-1]%MO, fac[i] = 1ll*fac[i-1]*i%MO, facinv[i] = 1ll*facinv[i-1]*facinv[i]%MO; 29 f[1][1][1] = 1; 30 for (int i=2; i<=k+1; i++) 31 for (int t=i; t<=n; t++) 32 for (int l=1; l<=t-i+1; l++) 33 for (int p=1; p<=t-l-i+2; p++) 34 f[i][t][l] = (f[i][t][l]+1ll*f[i-1][t-l][p]*qmi(mi[p]-1, l)%MO*C(n-t+l, l)%MO*qmi(2, C(l, 2))%MO)%MO; 35 for (int i=1; i<=n; i++) 36 for (int j=1; j<=n; j++) 37 if (f[k+1][i][j]) 38 ans = (ans+1ll*f[k+1][i][j]*j%MO*qmi(2, C(n-i, 2))%MO*qmi(2, 1ll*j*(n-i)%MO))%MO; 39 printf("%lld ",1ll*ans*qmi(n-1, MO-2)%MO); 40 return 0; 41 }
END