表示“必须选”的模型
题目大意
题目分析
一个格子有四种方式看上去很难处理。将横竖两个方向分开考虑,会发现:因为收益只与相邻格子是否连通有关,所以可以将一个格子拆成表示横竖两个方向的,互相独立的点。
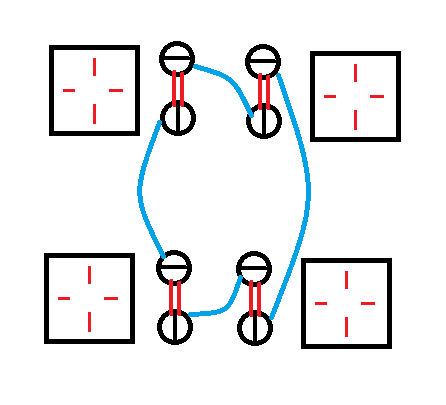
上图的格子里四个方向红边表示的就是一个格子的可能方向;拆点后所连蓝边的容量为1,费用即为连通两个格子的收益。
但是这样建图不能够表示某些格子必须要选。
考虑一个格子如果被选择了会发生什么:因为每个格子都处在环上,那么被选择的网格一定可以通过其他节点走到汇点。这意味着一个格子拆成的两个节点之间的边就可以先不建,而若最大流不等于网格总数,即有节点不可能被合法选中。
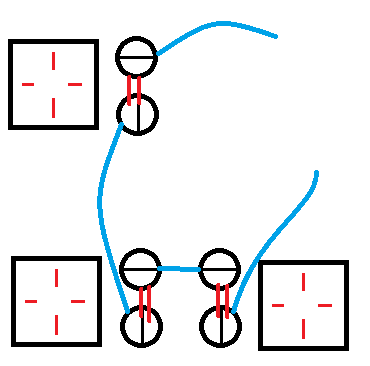
建图的时候一定要先理解清楚,因为有很多种错误方式,下图就是其中一个。
1 #include<queue> 2 #include<cstdio> 3 #include<cctype> 4 #include<cstring> 5 #include<algorithm> 6 const int maxn = 2035; 7 const int maxm = 100035; 8 const int INF = 2e9; 9 10 struct Edge 11 { 12 int u,v,f,c,cst; 13 Edge(int a=0, int b=0, int c=0, int d=0, int e=0):u(a),v(b),f(c),c(d),cst(e) {} 14 }edges[maxm]; 15 int sne,n,m,S,T; 16 bool ess[33][33],inq[maxn]; 17 int tagl[33][33],tagr[33][33],valc[33][33],valr[33][33]; //tagl为入点,tagr为出点 18 int edgeTot,head[maxn],nxt[maxm],flw[maxn],cst[maxn],bck[maxn]; 19 20 int read() 21 { 22 char ch = getchar(); 23 int num = 0, fl = 1; 24 for (; !isdigit(ch); ch=getchar()) 25 if (ch=='-') fl = -1; 26 for (; isdigit(ch); ch=getchar()) 27 num = (num<<1)+(num<<3)+ch-48; 28 return num*fl; 29 } 30 void addedge(int u, int v, int c, int cst) 31 { 32 edges[edgeTot] = Edge(u, v, 0, c, cst), nxt[edgeTot] = head[u], head[u] = edgeTot++; 33 edges[edgeTot] = Edge(v, u, 0, 0, -cst), nxt[edgeTot] = head[v], head[v] = edgeTot++; 34 } 35 void maxFlow() 36 { 37 int mxFlw = 0, cost = 0; 38 for (;;) 39 { 40 std::queue<int> q; 41 memset(flw, 0, sizeof flw); 42 memset(bck, 0, sizeof bck); 43 memset(cst, 0x3f3f3f3f, sizeof cst); 44 q.push(S), flw[S] = INF, cst[S] = 0; 45 for (int tmp; q.size(); ) 46 { 47 tmp = q.front(), q.pop(), inq[tmp] = 0; 48 for (int i=head[tmp]; i!=-1; i=nxt[i]) 49 { 50 int v = edges[i].v; 51 if (cst[tmp]+edges[i].cst < cst[v]&&edges[i].f < edges[i].c){ 52 bck[v] = i, cst[v] = cst[tmp]+edges[i].cst; 53 flw[v] = std::min(flw[tmp], edges[i].c-edges[i].f); 54 if (!inq[v]) inq[v] = 1, q.push(v); 55 } 56 } 57 } 58 if (!flw[T]) break; 59 for (int i=T; i!=S; i=edges[bck[i]].u) 60 edges[bck[i]].f += flw[T], edges[bck[i]^1].f -= flw[T]; 61 mxFlw += flw[T], cost += cst[T]*flw[T]; 62 } 63 if (mxFlw!=n*m) puts("Impossible"); 64 else printf("%d ",-cost); 65 } 66 int main() 67 { 68 sne = read(); 69 for (int cse=1; cse<=sne; cse++) 70 { 71 printf("Case #%d: ",cse); 72 memset(ess, 0, sizeof ess); 73 memset(head, -1, sizeof head); 74 edgeTot = 0, n = read(), m = read(); 75 for (int i=1; i<=n; i++) 76 for (int j=1; j<m; j++) 77 valc[i][j] = read(); 78 for (int i=1; i<n; i++) 79 for (int j=1; j<=m; j++) 80 valr[i][j] = read(); 81 for (int i=1, cnt=0; i<=n; i++) 82 for (int j=1; j<=m; j++) 83 tagl[i][j] = ++cnt, tagr[i][j] = ++cnt; 84 S = 0, T = tagr[n][m]+1; 85 for (int i=1; i<=n; i++) 86 for (int j=1; j<=m; j++) 87 if ((i+j)&1){ //为避免重复建边的处理技巧 88 if (j+1 <= m) addedge(tagl[i][j], tagr[i][j+1], 1, -valc[i][j]); 89 if (j-1 >= 1) addedge(tagl[i][j], tagr[i][j-1], 1, -valc[i][j-1]); 90 }else{ 91 if (i+1 <= n) addedge(tagl[i][j], tagr[i+1][j], 1, -valr[i][j]); 92 if (i+1 >= 1) addedge(tagl[i][j], tagr[i-1][j], 1, -valr[i-1][j]); 93 } 94 for (int i=read(); i; i--) ess[read()][read()] = 1; 95 for (int i=1; i<=n; i++) 96 for (int j=1; j<=m; j++) 97 { 98 addedge(S, tagl[i][j], 1, 0); 99 addedge(tagr[i][j], T, 1, 0); 100 if (!ess[i][j]) addedge(tagl[i][j], tagr[i][j], 1, 0); 101 } 102 maxFlow(); 103 } 104 return 0; 105 }
END
