Sigmoid函数(也叫逻辑斯谛函数)由下列公式定义:
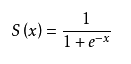
其对x的导数可以用自身表示:
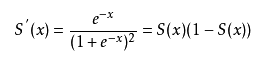
相关代码:
def nonlin(x, deriv=False): if(deriv): return x*(1-x) return 1/(1+np.exp(-x))
Sigmoid函数的图形如S曲线:

1.在神经网络中sigmoid通常被用作激活函数,它可以用来处理二分类问题。那么什么是激活函数呢?
我们知道在多层的神经网络中,上一层的信号(也就是wx+b算出的结果y)要作为下一层的输入,但是这个上一层的信号在输入到下一层之前需要一次激活f = sigmoid(y),因为
并不是所有的上一层信号都可以激活下一层,如果所有的上一层信号都可以激活下一层,那么这一层相当于什么都没有做。因此我需要选择一些信号激活下一层的神经元。如何表
示激活呢?就是当activation function的输出结果是0就代表抑制,是1就代表激活。因为按照下一层的神经元的计算wf+b来看,如果f接近于0,那么就会阻止x对应的权重起
作用,如果接近1,这个权重的作用会最大,在这个就是激活的含义。
2.可以很容易的抑制误差,尤其是相差比较大的误差。
在x=5的点和x=10的点原本相差很远(10-5=5)的点,在激活之后,也就是x=5和x=10对应的y坐标的值,相差的不大。比如说有一个噪声误差,在x=1000处,其他的点都分布
在x=5到x=10之间,那么sigmoid的函数就可以很好的去掉这种误差带来的影响。