原文链接:https://developers.google.com/machine-learning/crash-course/logistic-regression/
逻辑回归会生成一个介于 0 到 1 之间(不包括 0 和 1)的概率值,而不是确切地预测结果是 0 还是 1。
1- 计算概率
许多问题需要将概率估算值作为输出。
逻辑回归是一种极其高效的概率计算机制,返回的是概率(输出值始终落在 0 和 1 之间)。
可以通过如下两种方式使用返回的概率:
- “按原样”:“原样”使用返回的概率(例如,用户点击此广告的概率为 0.00023)。
- “转换成二元类别”:将返回的概率转换成二元值(例如,这封电子邮件是垃圾邮件)。
S型函数
S型函数会生成一个介于 0 和 1 之间的值。
定义:
$y = frac{1}{1 + e^{-z}}$
曲线图: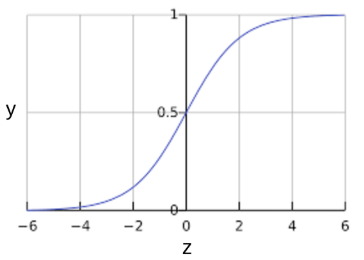
可以看出,S型函数的生成值恰好符合“逻辑回归返回的输出值范围”。
将S型函数应用在机器学习中,用数学方法表示为:
$y' = frac{1}{1 + e^{-(z)}}$
其中:
- y' 是逻辑回归模型针对特定样本的输出。
- z 表示使用逻辑回归训练的模型的线性层的输出,是 b + w1x1 + w2x2 + … wNxN
- w 的值是该模型学习的权重,b 是偏差。
- x 的值是特定样本的特征值。
此时,具有机器学习标签的 S 型函数的曲线图:

注意:z 也称为对数几率,因为 S 型函数的反函数表明,z 可定义为标签“1”的概率除以标签“0”的概率得出的值的对数: $z = log(frac{y}{1-y})$
2- 模型训练
逻辑回归的损失函数
线性回归的损失函数是平方损失。逻辑回归的损失函数是对数损失函数,定义如下:
$Log Loss = sum_{(x,y)in D} -ylog(y') - (1 - y)log(1 - y')$
其中:
- (xy)ϵD 是包含很多有标签样本 (x,y) 的数据集。
- “y”是有标签样本中的标签。由于这是逻辑回归,因此“y”的每个值必须是 0 或 1。
- “y'”是对于特征集“x”的预测值(介于 0 和 1 之间)。
逻辑回归中的正则化
正则化在逻辑回归建模中极其重要。
如果没有正则化,逻辑回归的渐近性会不断促使损失在高维度空间内达到 0。
因此,大多数逻辑回归模型会使用以下两个策略之一来降低模型复杂性:
- L2 正则化。
- 早停法,即,限制训练步数或学习速率。
假设向每个样本分配一个唯一 ID,且将每个 ID 映射到其自己的特征。
如果未指定正则化函数,模型会变得完全过拟合。
这是因为模型会尝试促使所有样本的损失达到 0 但始终达不到,从而使每个指示器特征的权重接近正无穷或负无穷。
当有大量罕见的特征组合且每个样本中仅一个时,包含特征组合的高维度数据会出现这种情况。
3- 总结
- 逻辑回归模型会生成概率。
- 对数损失函数是逻辑回归的损失函数。
- 逻辑回归被很多从业者广泛使用。
4- 关键词
二元分类 (binary classification)
一种分类任务,可输出两种互斥类别之一。
例如,对电子邮件进行评估并输出“垃圾邮件”或“非垃圾邮件”的机器学习模型就是一个二元分类器。
逻辑回归 (logistic regression)
一种模型,通过将 S 型函数应用于线性预测,生成分类问题中每个可能的离散标签值的概率。
虽然逻辑回归经常用于二元分类问题,但也可用于多类别分类问题(其叫法变为多类别逻辑回归或多项回归)。
S 型函数 (sigmoid function)
一种函数,可将逻辑回归输出或多项回归输出(对数几率)映射到概率,以返回介于 0 到 1 之间的值。
S 型函数的公式如下:
$y = frac{1}{1 + e^{-sigma}}$
在逻辑回归问题中, $sigma$非常简单:
$sigma = b + w_1x_1 + w_2x_2 + … w_nx_n$
换句话说,S 型函数可将 转换为介于 0 到 1 之间的概率。
在某些神经网络中,S 型函数可作为激活函数使用。
早停法 (early stopping)
一种正则化方法,是指在训练损失仍可以继续降低之前结束模型训练。
使用早停法时,您会在验证数据集的损失开始增大(也就是泛化效果变差)时结束模型训练。
对数损失函数 (Log Loss)
二元逻辑回归中使用的损失函数。
L1 正则化 (L₁ regularization)
一种正则化,根据权重的绝对值的总和来惩罚权重。
在依赖稀疏特征的模型中,L1 正则化有助于使不相关或几乎不相关的特征的权重正好为 0,从而将这些特征从模型中移除。
与 L2 正则化相对。
L2 正则化 (L₂ regularization)
一种正则化,根据权重的平方和来惩罚权重。
L2 正则化有助于使离群值(具有较大正值或较小负值)权重接近于 0,但又不正好为 0。
(与 L1 正则化相对。)在线性模型中,L2 正则化始终可以改进泛化。